Duck Pond Chances
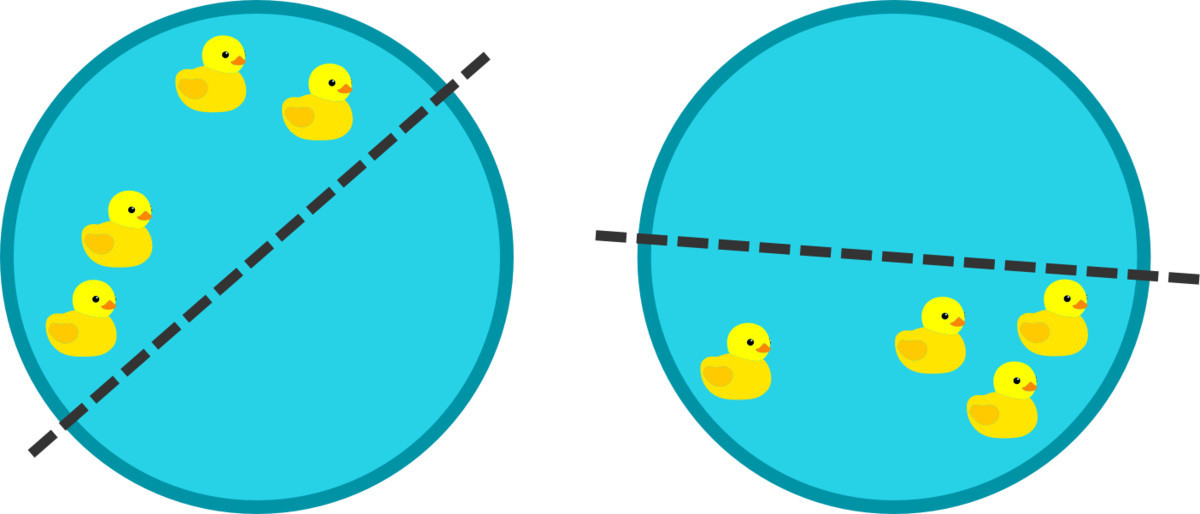
4 small ducks are in a large circular pond, and can each be at any point in the circle with equal chance. What is the probability that a diameter can be drawn so that all 4 ducks are in the same semicircle of the pond?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let's say, all 4 ducks represents 4 dots since they are small, inside a big circle; and the chance for 2 random dots to sit on a diameter of the circle is 0; and this is a level 2 question (this is important). Then with 2 random dots out of 4, you can always draw a diameters that can put those 2 dots inside the same half-circle (this is something you can prove).
Then, call the other 2 dots A and B. Since they are independent, the chance for A to stay in the same half-circle as the first two dots is 1/2, either it stays in the same one or it doesnt. It is the same for B, 1/2. Then the chance for all four of them should be 1/2 x 1/2 = 1/4
Log in to reply
I also though same
No, because in some of the ‘failed’ situations that you reject an entirely different diameter can be chosen that they are all on one side of. Your logic shows that the probability is at least 1/4, and an example of what I talk about shows that the probability is greater than 1/4.
If we extend this logic to find the probability of they will be in pond your logic will say n*(1)^(n-1)>1. Are you sure about correctness of this formula?
Log in to reply
Note that the generalized probability is 2 n − 1 n and not n − 1 n .
if the ducks are represented as dots, so that no line can slice the dot in two, there should really be only 3 ways to draw that line. It can either separate all the ducks on one side, zero on the other; leave one on one side, rest on the other, or 2 on each side. So three probable cases. I don't see the dilemma? Answer should be 1/3. Because really we don't care which ducks stay on witch side, just that all are on one
Log in to reply
That is a correct solution if we assume that all the ducks are the same and there are no way to distinguish them. When I think about it, if you separate them into duck A, duck B, duck C and duck D; the answer should be 1/8. It is quite interesting to see how a simple problem can have so many solutions base on how much you assume is true.
Log in to reply
Mine was 1/8 too, assuming ducks are not identical
Yes would be interested to see your proof :)
Log in to reply
Consider a radius vector drawn from the centre to the position of the duck and extend it to meet the circumference (if a duck happens to lie exactly on the centre then probability of that event is 0).In this way we can create a one-one mapping between the position of ducks and points on the circumference.Now the question has become as follows-What is the probability that n randomly chosen points on a circle lie on the same semicircle?So,suppose that the n points are numbered as 1,2,3....,we choose one point as a reference point,then the probability that a point lies within a distance of pi radians (while going clockwise) from the reference point is 1/2.Since this is true for all the remaining points ,the probability that the remaining (n-1) points are within a distance of pi radians from the reference point is (1/2)^(n-1).Since the events of choosing the initial first points are disjoint,the resultant probability can obtained by adding the probabilities of the n events,so we get the resultant probability as n*(1/2)^(n-1).
Log in to reply
Like it! Particularly the simplification of mapping the positions to points on the circumference :)
The mapping from position of duck to point on circumference is not necessarily one to one. Say for example if there are 2 ducks lying on the same radius vector, they are mapped to the same point on circumference, thus making the mapping not one to one.
Log in to reply
@Nicholas Leung – Just see the comments below.It has been explained that the probability of such event is 0.
I thought of it as a probability tree. Draw any diameter the chance 1 duck is on side a is 1/2. Chance duck 2 is on side a also 1/2 etc. Times together for each step the. Times by 2 for the chance all are on side a or all on side b I got 1/8.
I can't understand some of the other solutions answers although that might be the pain mess I'm on =P
Log in to reply
Yes that would be correct if the line was already fixed, but all on one side means we can set the dividing line after we see where all the ducks are ... that's why it is a tricky problem and the standard probability you mention does not apply
where ever the first two ducks are, a line can always be drawn so they are both in the same half.
Edit: P(3rd duck can be in one side of diameter)=3/4 P(4th duck)=2/3
Hence P(all 4 within one side of a diameter)=3/4 x 2/3=1/2
but how its 3/4 for 3rd duck and explain for p(4th duck) too
Log in to reply
I am also curious as to how it is 3/4 for 3rd duck as well. It seems to me that if the first 2 ducks are indeed in the same semi-circle (suppose they are on the dividing line), and you randomly dropped a duck into the pond, there would be a 50% chance that it would end up on either side of that line. A fourth duck would still have that same 50% chance, thus .5 x .5 would be 1/4.
Log in to reply
Because you can chose the dividing line, when you have 2 ducks there is on average a quarter of a ponds worth of movement in the dividing line, so third duck has 3/4 chance of being within the region you can chose your diameter. I agree it takes a bit of getting your head round but it is correct!
What if the first two ducks are on the diameter?
Log in to reply
if you look infinitely close you can always draw a diameter, that is why the small ducks and large pond is mentioned. I suppose you may have to "split hairs" ... or even feathers lol, but the answer tends to a half the larger the pond and the smaller the ducks
Log in to reply
With probability 0, there are ducks on the diameter. This is why such a case can be ignored.
I came to the conclusion that the probability is 3/4.... can you tell me where I went wrong? We can set up a coordinate system such that first duck has a polar angle of θ 1 = 0 and the second one has some polar angle 0 ≤ θ 2 ≤ π , with uniform probability. Now we can draw a diameter as required as long as the third duck has − θ 2 ≤ θ 3 ≤ π . On average, this is possible in 3 out of 4 cases.
Log in to reply
Edit: I agree P( for 3rd duck) =3/4, I have edited question, see below
I thought a little bit different. I made an imaginary diameter in the center of the circle, with four imaginary places. Two at each site. Then I imagined 4 together, 3+1, 2+2 and the probability of 4 then be at the same side. I got 12/12 on 4 together 4/12 on 3+1 4/12 on 2+2 Then 18/36 the sum.
That's 1/2
Was that right?
Ps: (1+1 is 0/12)
But, I have a different method. Assume all four ducks as one point. So, the required probability is [(pi r^2)/2]/(pi r^2)=1/2
I felt that Indraneel's explanation misses some details (though I trust he knows them), so I'm writing another (looong) one.
Firstly, we assume that all the points (ducks) are in general positions, specifically, no duck is in the center and no two ducks are collinear with the center of the pond.
Next, like Indraneel, we simplify the problem by realizing that we only care about the direction of each duck from the center of the pond, so each duck is basically assigned a random angle (say, between 0 to 360 degrees) and we want to know if the ducks fit within 180 degrees -- fix a direction, say clockwise. If the ducks fit in some semicircle, let us say that event E occurred. We want to know the probability of E occurring.
Now, we consider 4 events X 1 , X 2 , X 3 , X 4 , where X i is the event that the remaining 3 ducks are within 180 degrees of the i th duck in a clockwise direction.
Clearly, each X i is a subevent of E . What is not so obvious is that:
(1) The X i s are disjoint.
(2) E is (a subset of) the union of all X i s.
For (1), this is because if the 180 degrees after duck i contains the three other ducks, then another duck j cannot have duck i in the next 180 degrees of it. Thus the X i s are indeed disjoint.
For (2), suppose we have an interval of 180 degrees that contains all four angles. Then we can slide the interval clockwise until its boundary hits a duck (say duck i ). When that happens, the interval starts at duck i and contains the remaining three ducks. Thus, when E occurs, some X i occurs, so we have (2).
Now, as Indraneel did, we calculate the probability for X i . For any position of duck i , the probability of another duck j being in the next 180 degrees is 1/2, and since the positions of the ducks are mutually independent, we can multiply them to get 1/8.
Summing across all the X i s, we get the probability of E to be 4 * 1/8 = 1/2, as required.
Assume there are n ducks. Let's assume the "first" duck is at angle 0 ∘ in the semicircle (on the diameter). Then, there is a 2 1 chance that each other duck is in the semicircle, so there is a 2 n − 1 1 chance of the situation being a success.
However, any of the n ducks could be the "first" in the semicircle, and these are disjoint events, so the probability is n ⋅ 2 n − 1 1 = 4 ⋅ 8 1 = 2 1 .