Dynamic Geometry: P1

Geometry Level 3

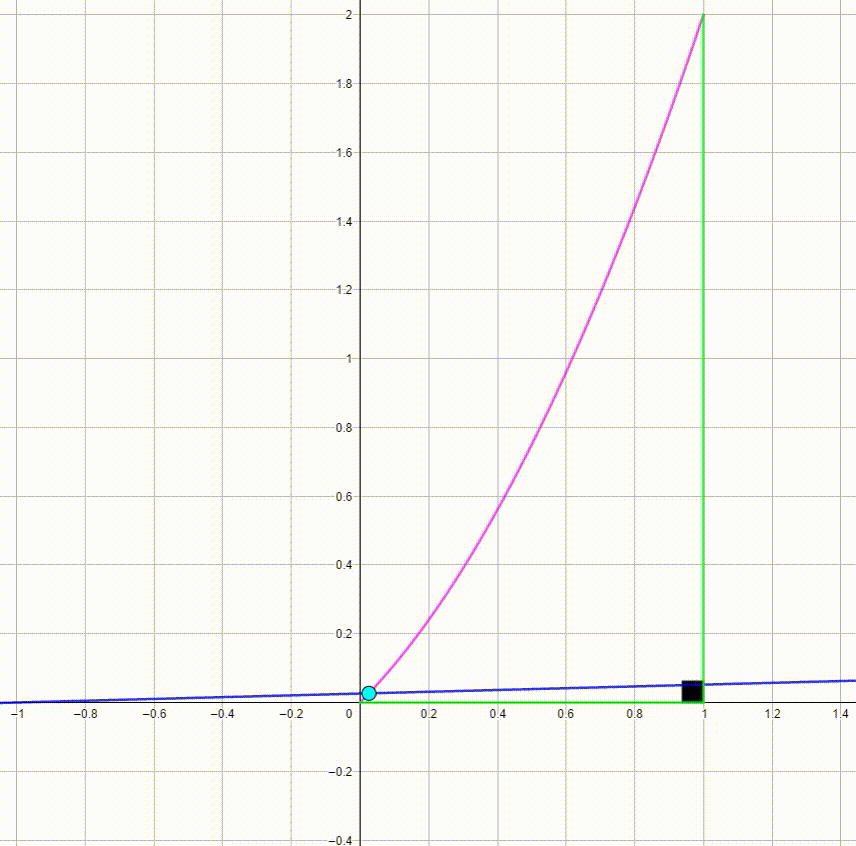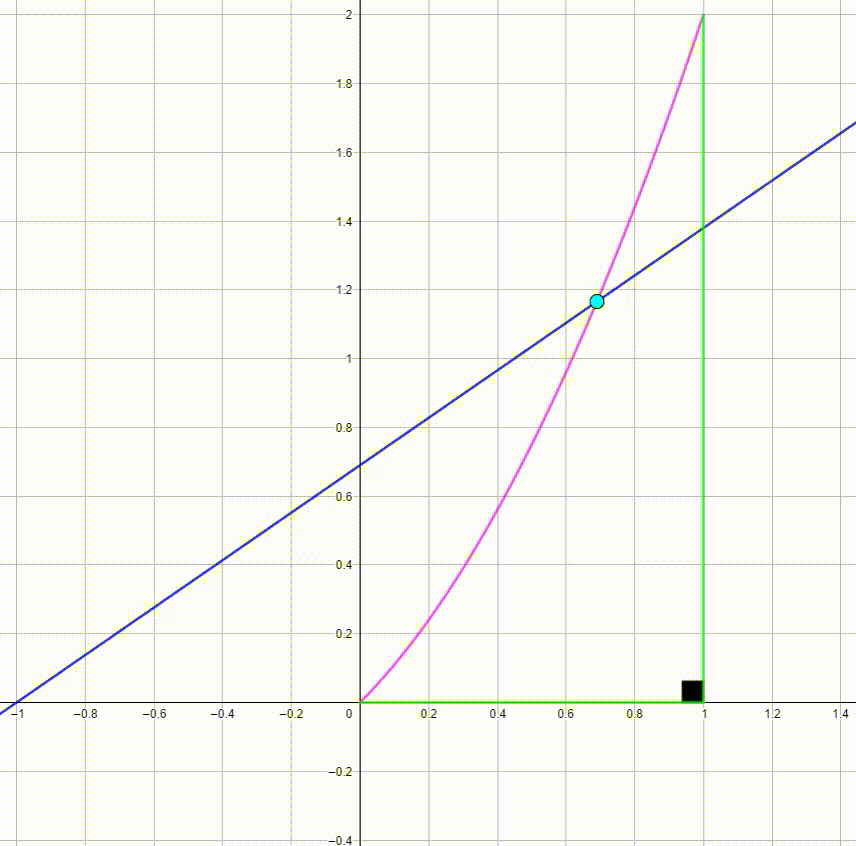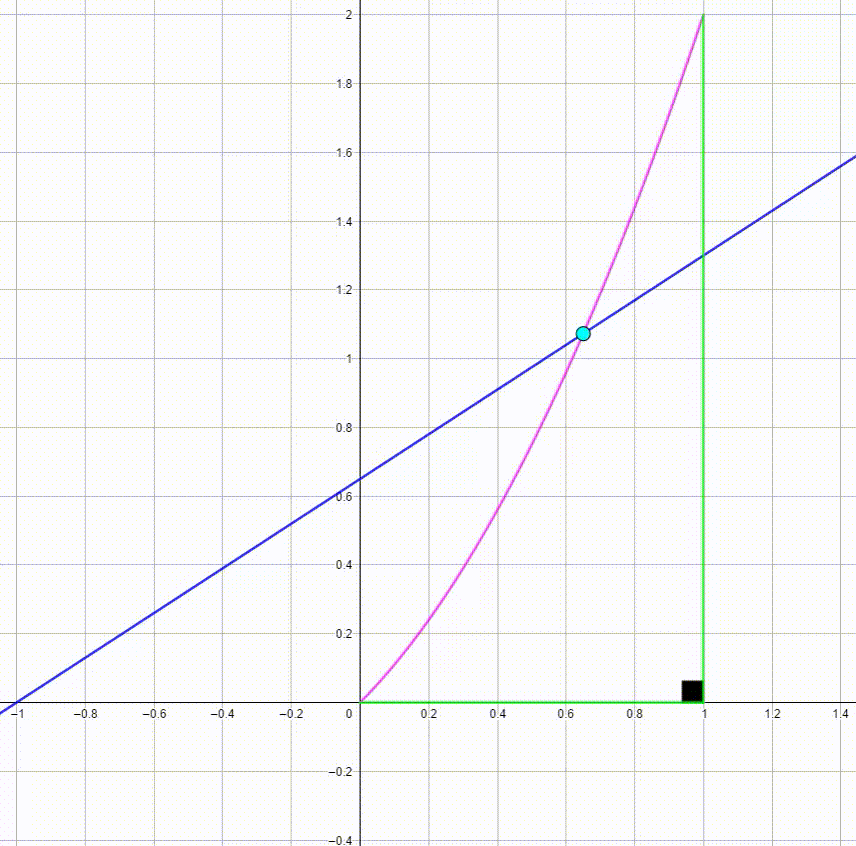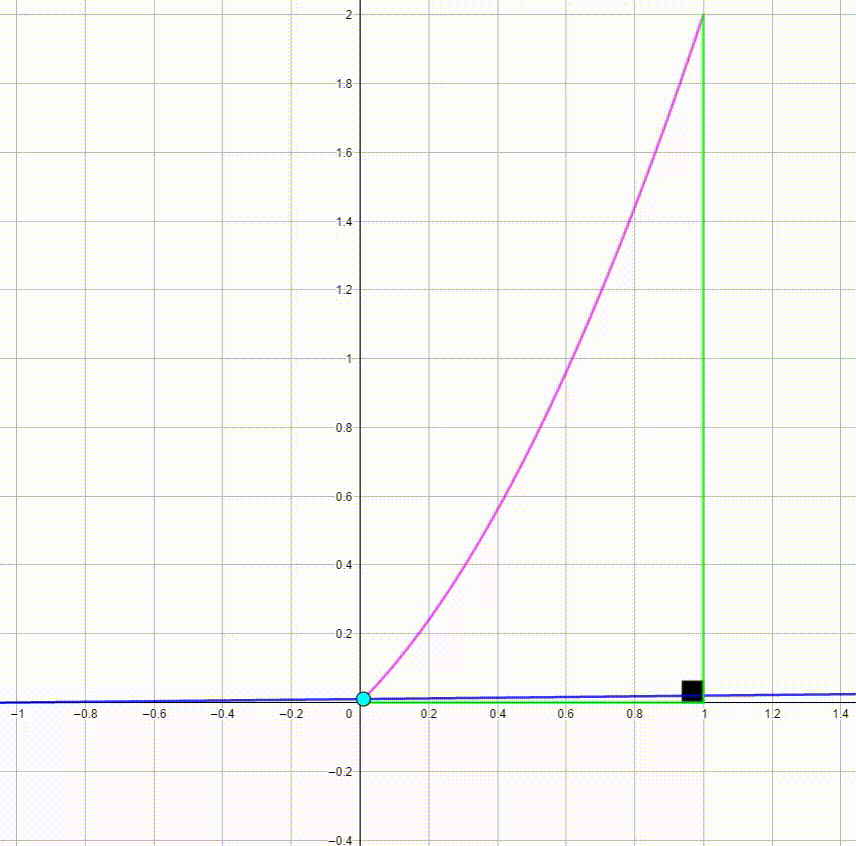
The diagram shows a blue line $y=ax+a$ and a cyan point $P(a;y_{p})$ with $0\le a\le 1$ . As $a$ varies from $0$ to $1$ and back from $1$ to $0$ , the cyan point moves along a pink curve. The black angle between the two green lines is a right angle. The area bounded by the pink curve and the green lines can be expressed as $\frac{b}{c}$ where $b$ , and $c$ are coprime positive integers. Find $2(c-b)$ .

The answer is 2.

1 solution

K T
Feb 1, 2021

The point $P$ on the line $y=ax+a$ has $a$ as its x-coordinate and therefore $y_p=a^2+a$ . The pink curve is (part of) the parabola with equation $y=x^2+x$ .

The area under the curve is found by evaluating the antiderivative: $A=\int_0^1 (x^2+x) dx=\frac{1}{3}x^3+\frac{1}{2}x^2 \bigg\rvert_0^1 =(\frac{1}{3}+\frac{1}{2}) - (0+0)=\frac{5}{6}$

The requested answer is $2(6-5)=\boxed{2}$

There is one thing that confuses me: I thought that in the question $y=ax+a$ instead of $ax+\alpha$ , so we don’t need to find the relationship between $a$ and $\alpha$ , do we?

Jeff Giff - 4 months, 1 week ago

Or is it because of the question being edited?

Jeff Giff - 4 months, 1 week ago

Hi, the slope of the line and its y intercept are the same and i called it "a", that's it.

Valentin Duringer - 4 months, 1 week ago

@Valentin Duringer ,could you collect the link of all these dynamic geometry questions into a note? I’d like to include it to my RadMaths note :)

Jeff Giff - 4 months, 1 week ago

How do I do this? I have never done it before... ;)

Valentin Duringer - 4 months, 1 week ago

You could create a discussion :) in the discussion use format [ text ] ( link ) without the spaces to link the questions :)

Jeff Giff - 4 months, 1 week ago

Never mind I’ll do that :)

Jeff Giff - 4 months, 1 week ago

@Jeff Giff – Cool, just one quick note, i'm about the post 100 problems in the series, I already created them.

Valentin Duringer - 4 months, 1 week ago

@Valentin Duringer – Oh, my, god that is awesome!

Jeff Giff - 4 months, 1 week ago

@Jeff Giff Thanks for pointing that out. I may have misread an 'a' as an 'α', not sure! It is 'a' now, which is best anyway. I edited the solution accordingly, to avoid any further confusion. Took the chance to edit other parts too.

K T - 4 months, 1 week ago

Nice! But in the fourth line, before the third ‘=‘, shouldn’t it read $\displaystyle | ^1 _0$ ?

Jeff Giff - 4 months, 1 week ago

Yes, I think I was still editing had some trouble scaling the bar. I believe it's ok now

K T - 4 months, 1 week ago