Dynamic Geometry: P11
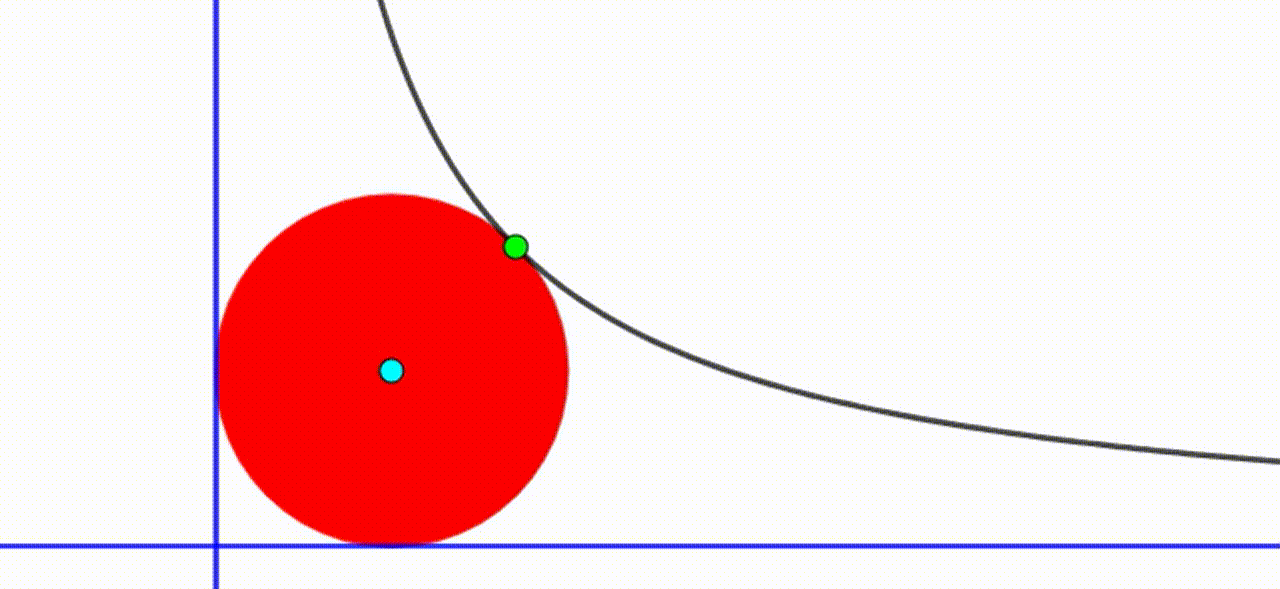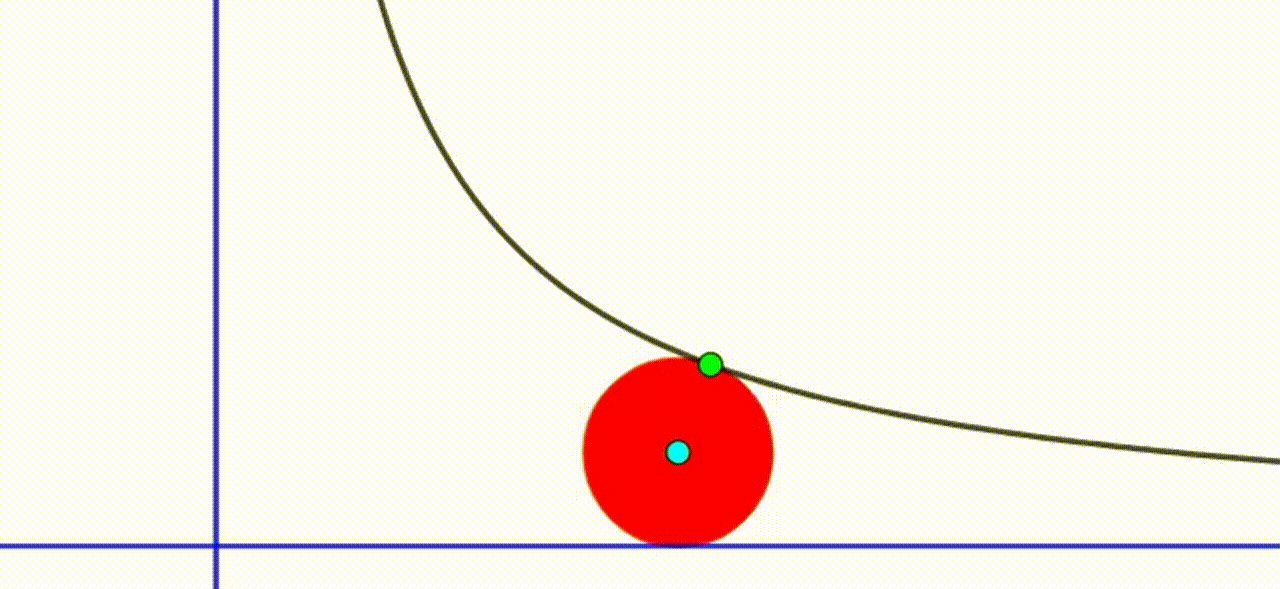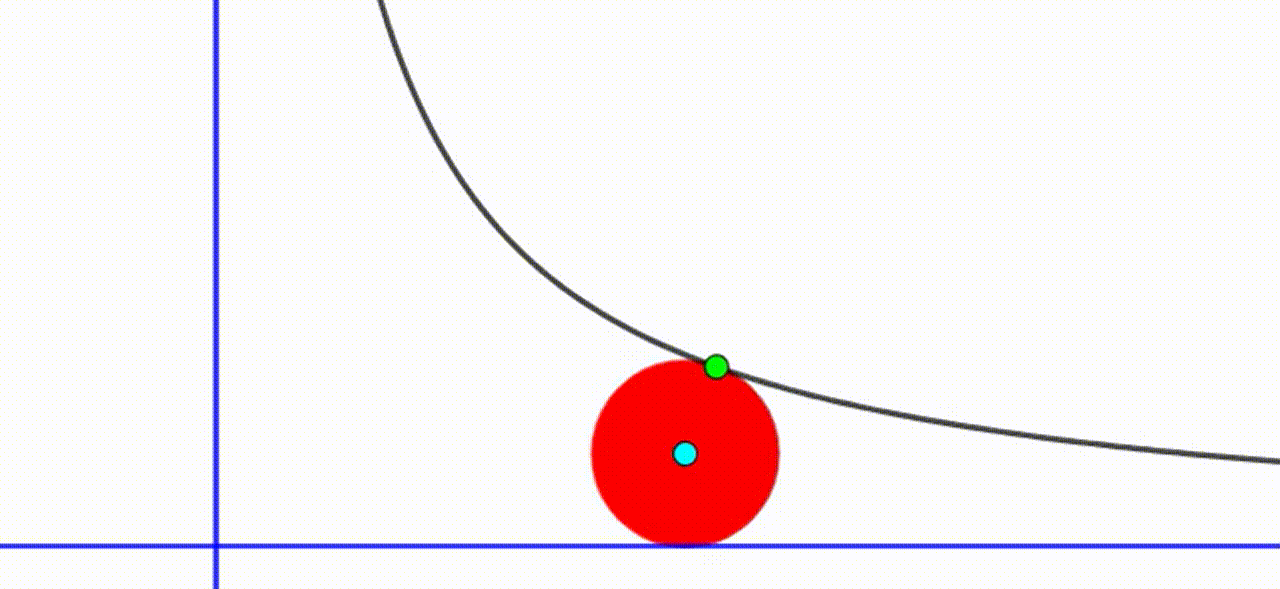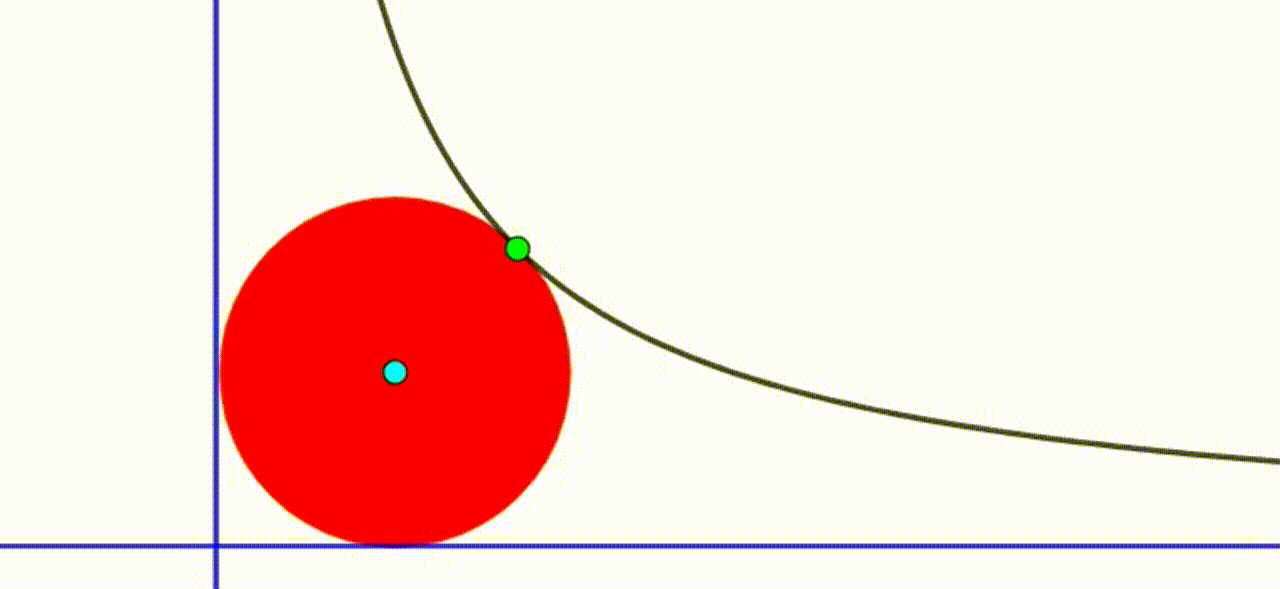 The diagram shows a black curve
y
=
x
1
and a red circle moving so that it's tangent to the black curve and to the blue line
y
=
0
. When the ratio of the
x
-coordinate to the
y
-coordinates of the circle's center (cyan) is equal to
5
9
, the ratio of the
x
-coordinate to the
y
-coordinates of the tangency point (green) between the black curve and the red circle can be expressed as
b
c
where
c
and
b
are coprime positive integers. Find
c
+
b
.
The diagram shows a black curve
y
=
x
1
and a red circle moving so that it's tangent to the black curve and to the blue line
y
=
0
. When the ratio of the
x
-coordinate to the
y
-coordinates of the circle's center (cyan) is equal to
5
9
, the ratio of the
x
-coordinate to the
y
-coordinates of the tangency point (green) between the black curve and the red circle can be expressed as
b
c
where
c
and
b
are coprime positive integers. Find
c
+
b
.
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Nice solution, Valentin! I finally got around to solving this guy today :)
Log in to reply
Thanks, the only issue is that it involves a calculator for the tricky equation xc/yc (I'm not that smart). Please share P23 and P25 as it's still unrated. I'm going to post more problems today !
Log in to reply
Oh it is not that hard to solve :) we are looking for
a
1
a
=
a
2
. Let
m
=
a
2
.
The equation:
a
1
+
m
2
−
m
1
+
m
2
a
2
m
−
1
+
m
2
=
5
9
.
So
1
0
m
−
5
1
+
m
2
=
9
+
9
m
2
−
9
m
1
+
m
2
.
Log in to reply
@Jeff Giff – Well, I'm just lazy then. I'm not too much in algebra, even though I should
Log in to reply
@Valentin Duringer – Yup I understand... since it is easier to use Wolphram or GeoGebra :P
Log in to reply
@Jeff Giff – You caught me, also, I try to make problems that are almost always solvable manually in this series
Excellent solution!
Log in to reply
Thank you Jeff ! Please share P23 and P25 as they are still unrated ! I'll post more today !
Log in to reply
Log in to reply
@Jeff Giff – @Jeff Giff I create about 5-10 problems for this series per day. But I can only post 3-4 per day max becasue otherwise, the big volume would not be seen by members, that would be a shame.
@Jeff Giff I posted more problem and I will post more today, please share, I hope you'll like them !
I already did it's awesome !
We know that this line will be perpendicular to the radius of the circle. We can calculate then the line where lies the center of the circle. We get y = a 2 ⋅ x + a 1 − a 4 . Then we establish the coordinate of point M ( 2 a ; 0 ) , the intersection point between the x axis and the tangent line.
Since the x axis and the tangent line are both tangent to the circle, the distance between A and M are the same as the horizontal distance between M and C , the center of the circle.
We can express the distance A M in terms of a : A M = ( a − 2 a ) 2 + ( a 1 ) 2 = a a 4 + 1
We can now report this distance on the x axis and find that the x -coordinate of center of the circle is 2 a − a a 4 + 1 = a 2 a 2 − a 4 + 1
We can now find the intersection point between the lines y = a 2 ⋅ x + a 1 − a 4 and x = a 2 a 2 − a 4 + 1 .
We find C ( a 2 a 2 − 1 + a 4 ; a 1 + a 4 − a 2 1 + a 4 )
Then we solve y C x C = 5 9 in terms of a and find a = 3 2
Finally a 1 a = a 2 = 3 4 and 3 + 4 = 7