Dynamic Geometry: P16
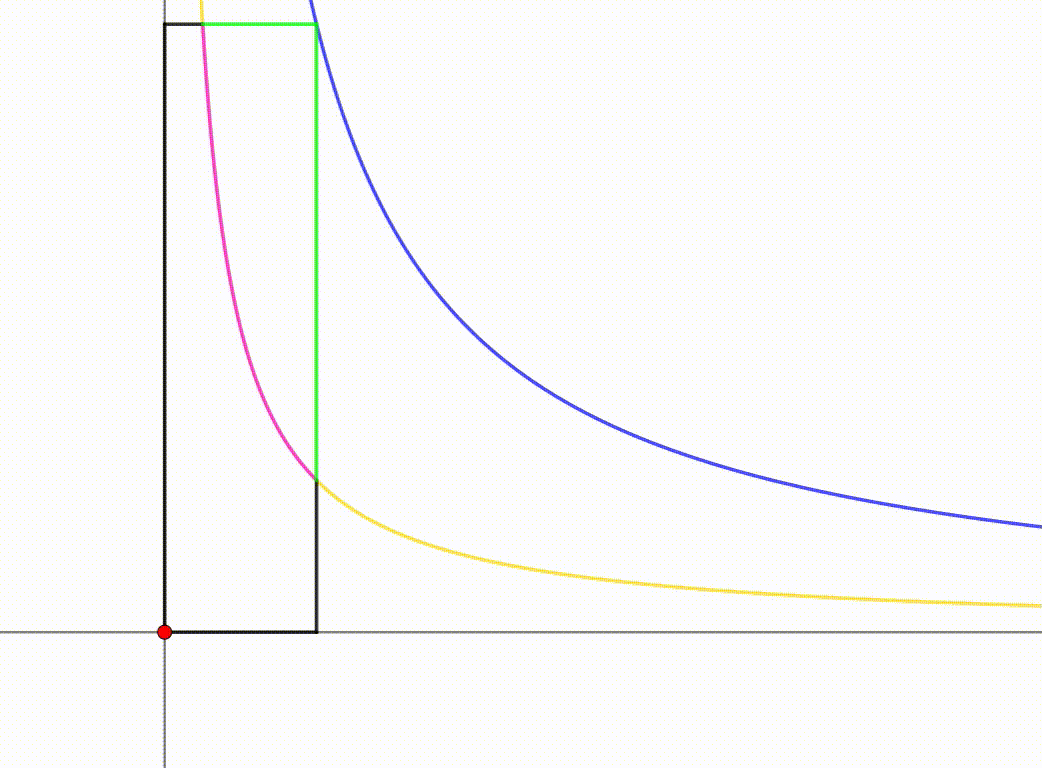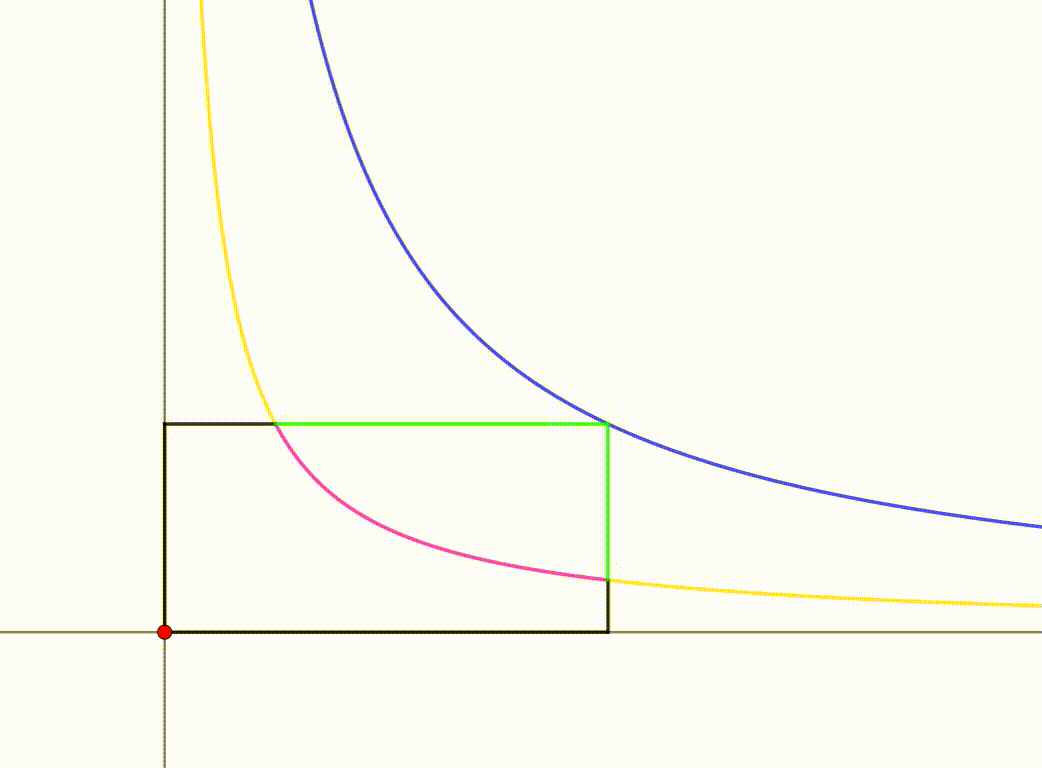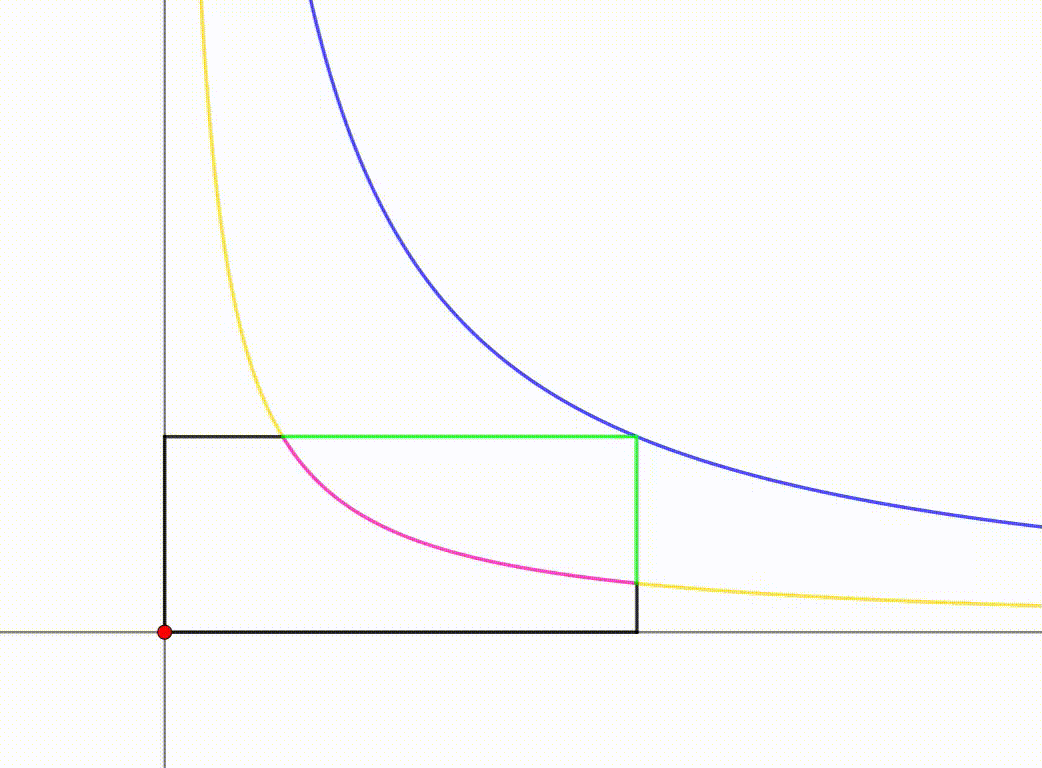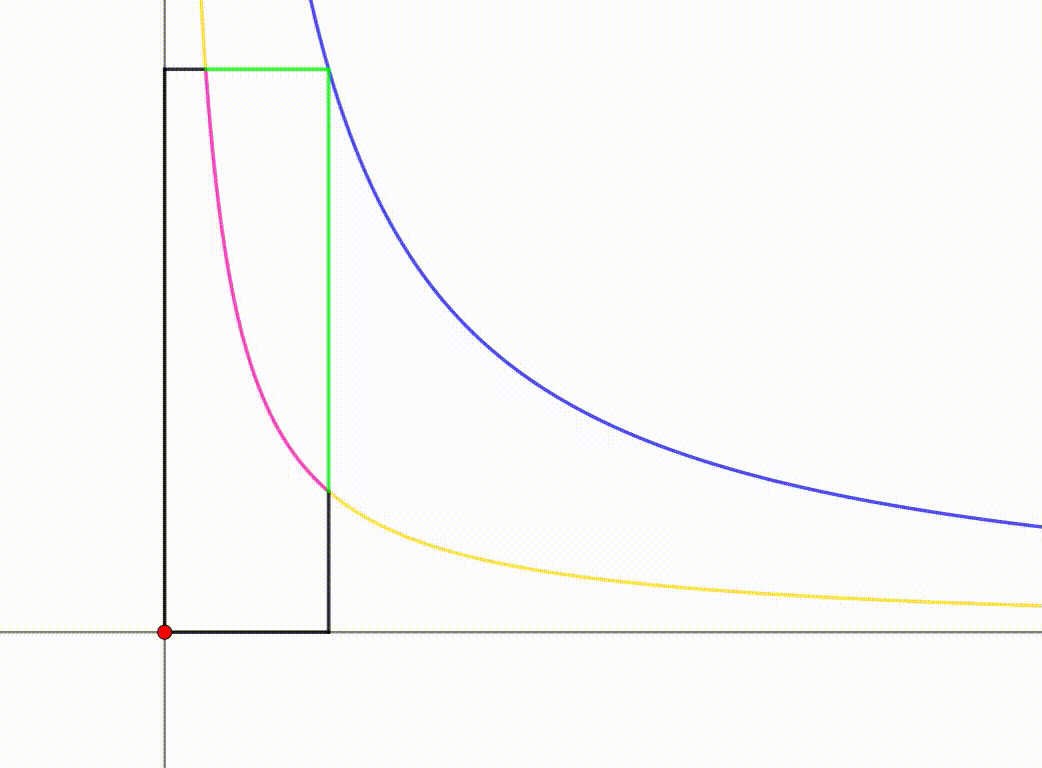
A variable rectangle has its bottom-left vertex at the origin ( 0 , 0 ) of the x y -plane and its top-right vertex on the curve y = x 1 (blue) for x > 0 . As the top-right vertex moves along y = x 1 , the center of the rectangle forms a locus (colored in yellow outside the rectangle and pink in the rectangle).
When the sum of the area and perimeter of the rectangle is minimum , the area enclosed by the pink curve and the green sides of the rectangle can be expressed as:
c a − b ln b
where a , b , and c are positive integers and b is a prime. Find a + b + c .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Thanks for posting Tom !
Log in to reply
No prob, Valentin! These dynamic geometry problems are a treat to solve.
Log in to reply
Im glad you liked them !Get ready because i made 100 of them ! I ll try to post at least 5 a day. If you have the time to post your solution to some of the others currently unsolve problems dont hesitate!
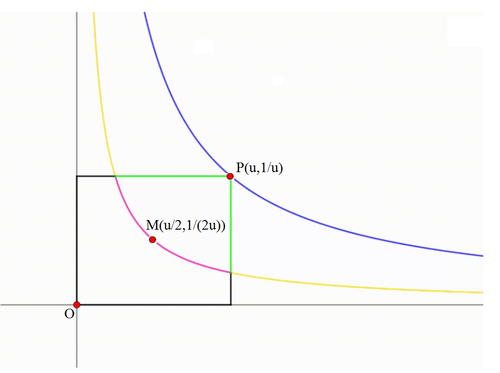
Consider a point P ( u , u 1 ) on y = x 1 . Then the rectangle formed has side lengths u and u 1 . The center of the rectangle is then M = ( 2 u , 2 u 1 ) . Replacing 2 u with x , we get M ( x , 4 x 1 ) . Therefore the equation of the locus of rectangle's center is y = 4 x 1 .
The sum of area and perimeter of the rectangle is given by x ⋅ x 1 + 2 x + x 2 . By AM-GM inequality :
1 + 2 ( x + x 1 ) ≥ 1 + 2 x ⋅ x 1 = 3
Equality or the area and perimeter is minimum when x = x 1 = 1 . Then the locus cuts the top side of the rectangle at y = 1 = 4 x 1 ⟹ x = 4 1 and the right side of the rectangle at x = 1 and y = 4 1 . Then the area bounded by the locus and the top-right corner of the rectangular is:
∫ 4 1 1 ( 1 − 4 x 1 ) d x = x − 4 1 ln x ∣ ∣ ∣ ∣ 4 1 1 = 4 3 − 4 ln 4 = 4 3 − 2 ln 2
Therefore, a + b + c = 3 + 2 + 4 = 3 .
@Valentin Duringer , I have edited the problem. You can take a look.
Log in to reply
I need to know how to write a fraction in "normal" size...
Log in to reply
When you use \ [ \ ] , everything within is normal size. For \ ( \ ) add \displaystyle in front \displaystyle \frac 12 \sum {n=1}^\infty \int \frac 14^\frac 12 2 1 n = 1 ∑ ∞ ∫ 4 1 2 1 . For \frac \pi 2 2 π use \dfrac \pi 2 2 π . also \binom mn ( n m ) use \dbinom mn ( n m ) . d for display.
Let ( x 0 , x 0 1 ) be an arbitrary point on the blue curve y = x 1 . The traveling rectangle has its center parametrically described as:
x = 2 x 0 ,
y = 2 x 0 1
which traces the yellow curve y = 4 x 1 . If we desire to compute the minimum sum of the rectangular perimeter and area, we can model this relationship as f ( x ) = 2 x + x 2 + ( x ) ( 1 / x ) = 2 x + x 2 + 1 whose first derivative (equal to zero) yields:
f ′ ( x ) = 2 − x 2 2 = 0 ⇒ x = 1
and second derivative at x = 1 yields:
f ′ ′ ( x ) = x 3 4 ⇒ f ′ ′ ( 1 ) = 4 > 0 (a global minimum is attained when the rectangle is a unit square at the point ( 1 , 1 ) on the blue curve).
The line y = 1 intersects the yellow curve at x = 4 1 , and the area bounded between the rectangle and the pink segment of y = 4 x 1 is computed per:
∫ 1 / 4 1 1 − 4 x 1 d x ⇒ x − 4 1 ln ( x ) ∣ 1 / 4 1 = 4 3 − ln ( 4 ) = 4 3 − 2 ln ( 2 )
which yields a = 3 , b = 2 , c = 4 ⇒ a + b + c = 3 .