Dynamic Geometry: P3
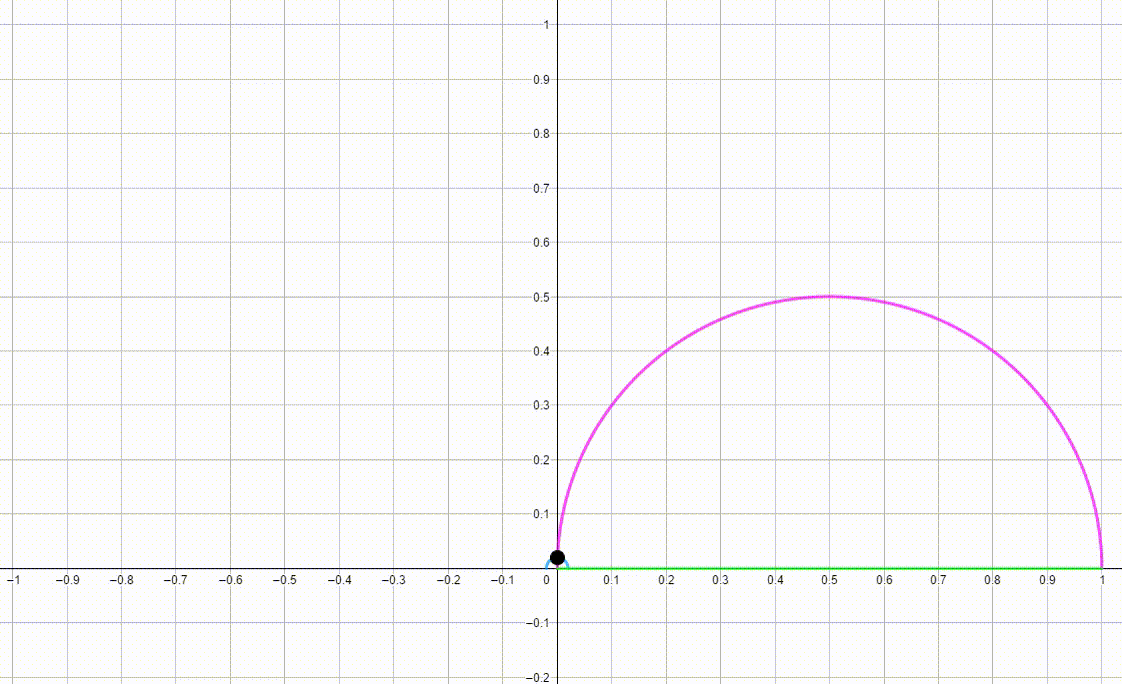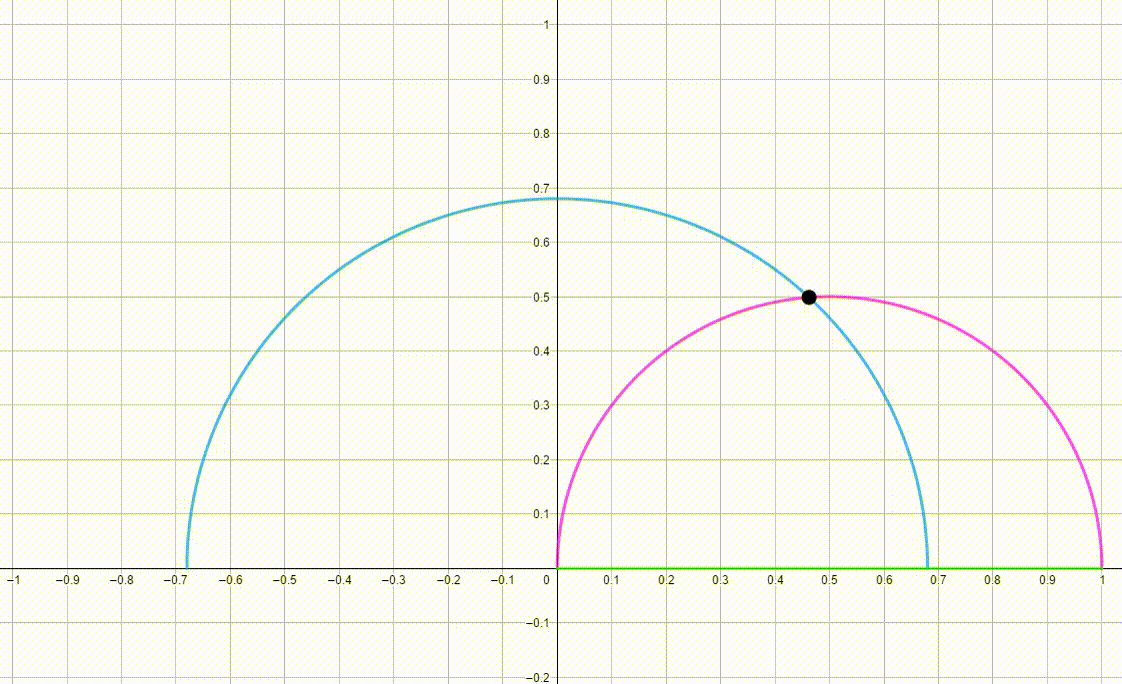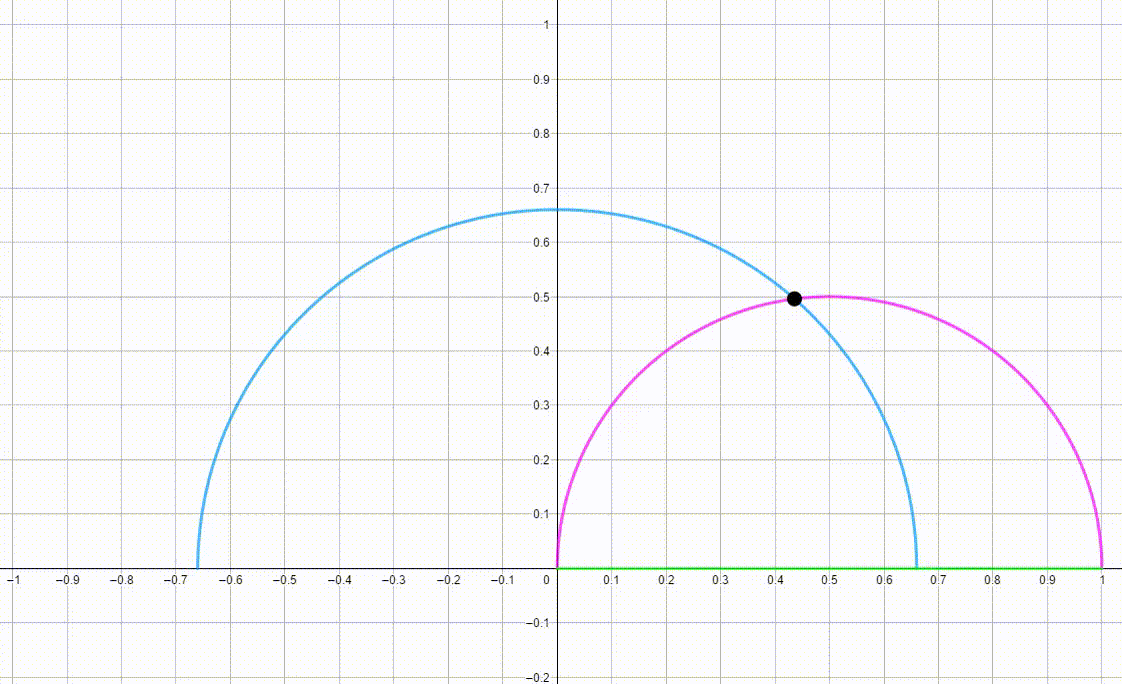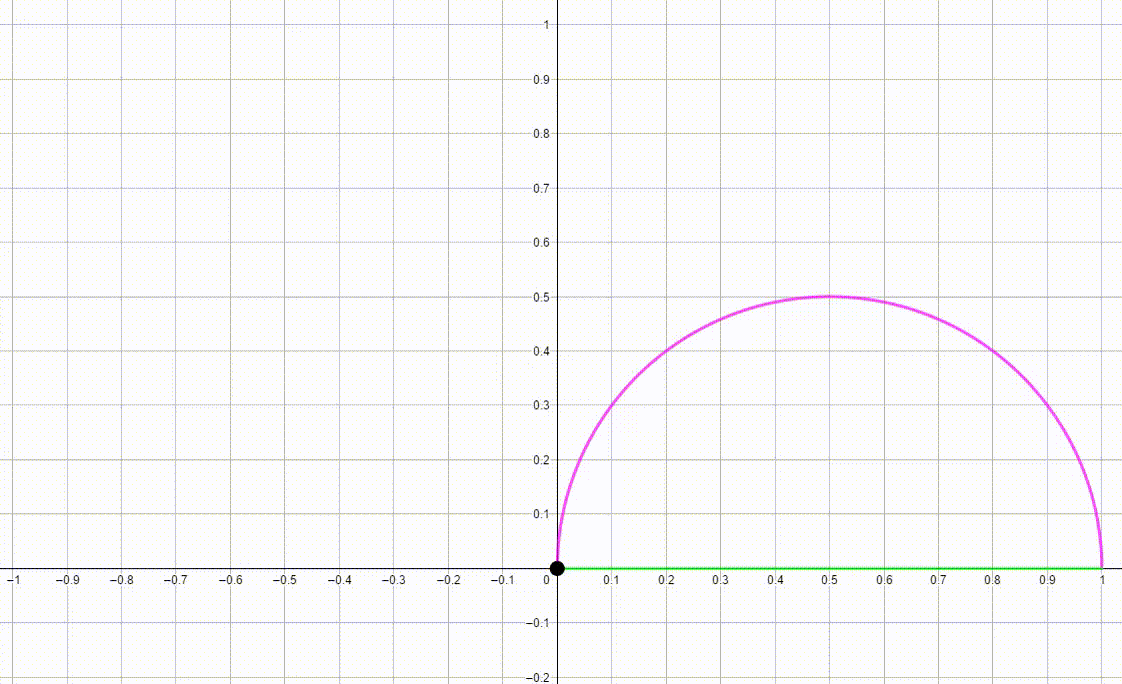 The diagram shows a blue semicircle
y
=
a
2
−
x
2
and a black point
P
(
a
2
;
a
2
−
a
4
)
with
0
≤
a
≤
1
. As
a
varies from
0
to
1
and back from
1
to
0
, the black point moves along a pink curve. The area bounded by the pink curve and the green line can be expressed as
b
π
where
b
is a positive integer. Find
⌈
π
⌉
+
b
.
The diagram shows a blue semicircle
y
=
a
2
−
x
2
and a black point
P
(
a
2
;
a
2
−
a
4
)
with
0
≤
a
≤
1
. As
a
varies from
0
to
1
and back from
1
to
0
, the black point moves along a pink curve. The area bounded by the pink curve and the green line can be expressed as
b
π
where
b
is a positive integer. Find
⌈
π
⌉
+
b
.
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Thanks for posting, what was inaccurate?
It is mentioned in the text - the coordinates you specify for P and also the expression 8 π should be given as a π
Log in to reply
oh that was corrected of course
Log in to reply
I think you still need to look at P ( a 2 ; a 2 − a 4 )
Done, thanks !
Good explanation! But how do I find the antiderivative to y = x − x 2 ?
Log in to reply
Maybe the easiest way to do the integral is to do a substitution u = x − 2 1 so that ∫ 0 1 x − x 2 d x becomes ∫ − 2 1 2 1 4 1 − u 2 d u = 2 1 ∫ − 2 1 2 1 1 − 4 u 2 d u and do a second sub v = 2 u to arrive at 4 1 ∫ − 1 1 1 − v 2 d v .
Log in to reply
Oic! Thanks! :)
Log in to reply
@Jeff Giff – I added this to the solution Thank you for asking and thus helping improve the solution.
The problem contained some inaccuracies. So I had to guess what was intended.
From the equation y = a 2 − x 2
it follows that if you fill in x = a 2 you get P = ( a 2 ; a 2 − a 4 ) (Originally a square root was missing here in the problem - fixed now). In terms of x you get: P = ( x ; x − x 2 )
This is the equation of the pink curve. We want the area A = ∫ 0 1 x − x 2 d x Maybe the easiest way to do the integral is to do a substitution u = x − 2 1 so that the integral becomes ∫ − 2 1 2 1 4 1 − u 2 d u = 2 1 ∫ − 2 1 2 1 1 − 4 u 2 d u and do a second sub v = 2 u to arrive at 4 1 ∫ − 1 1 1 − v 2 d v which corresponds to 4 1 of the area of half a unit circle.
Alternatively, this integral could be solved using a third sub v = sin ( w ) , via ∫ − 2 π 2 π cos ( w ) d sin w = ∫ − 2 π 2 π cos 2 ( w ) d w = ∫ − 2 π 2 π ( 2 1 cos ( 2 w ) + 2 1 ) d w = 2 1 cos π + 4 1 π − 2 1 cos ( − π ) − 4 1 ( − π ) ) = 2 1 π .
Either way A = 8 π
This answer was originally given literally (without any b in the expression!) so I guessed that b π was intended and submitted ⌈ π ⌉ + b = 4 + 8 = 1 2
Edit 1: In the new version of the problem this was corrected, I renamed my a accordingly to b .
Edit 2: Explained the integration (in response to Jeff Giff's question)