Dynamic Geometry: P9
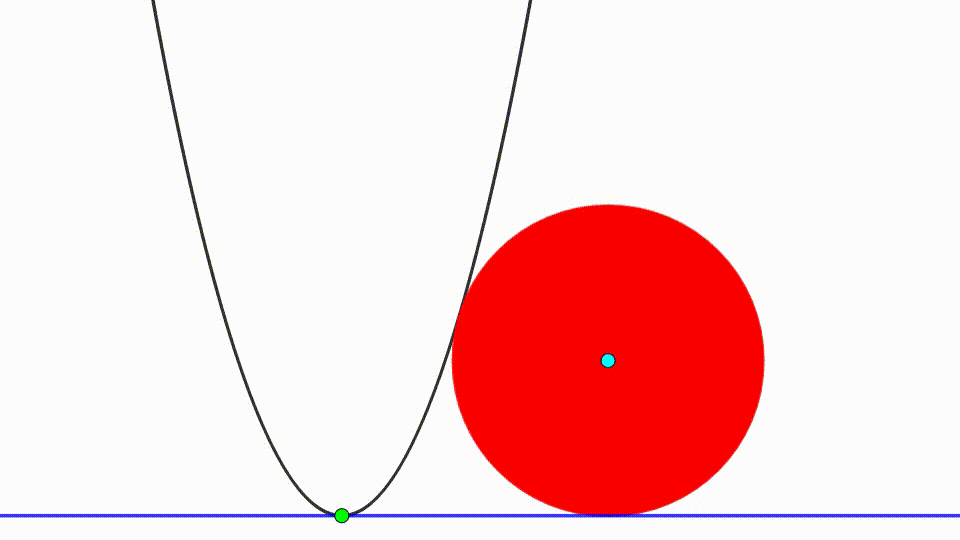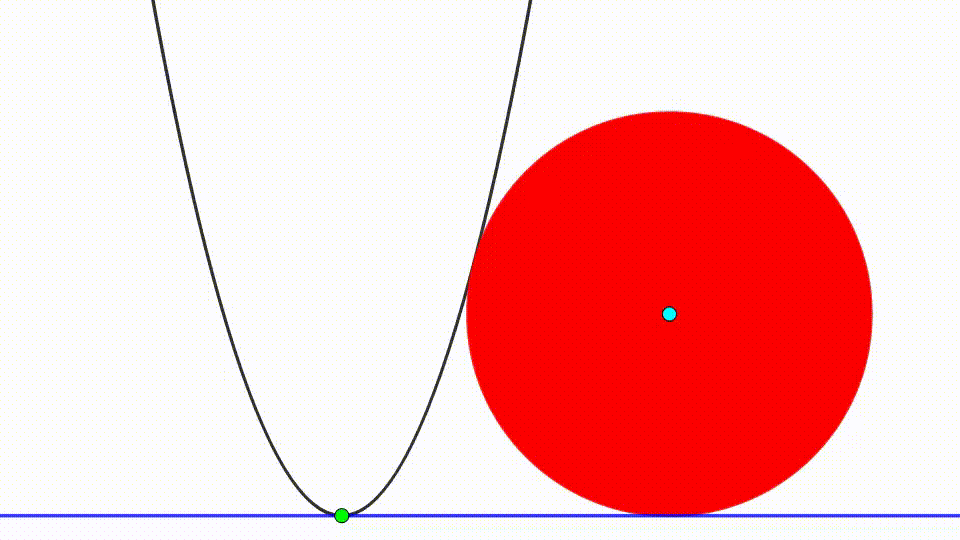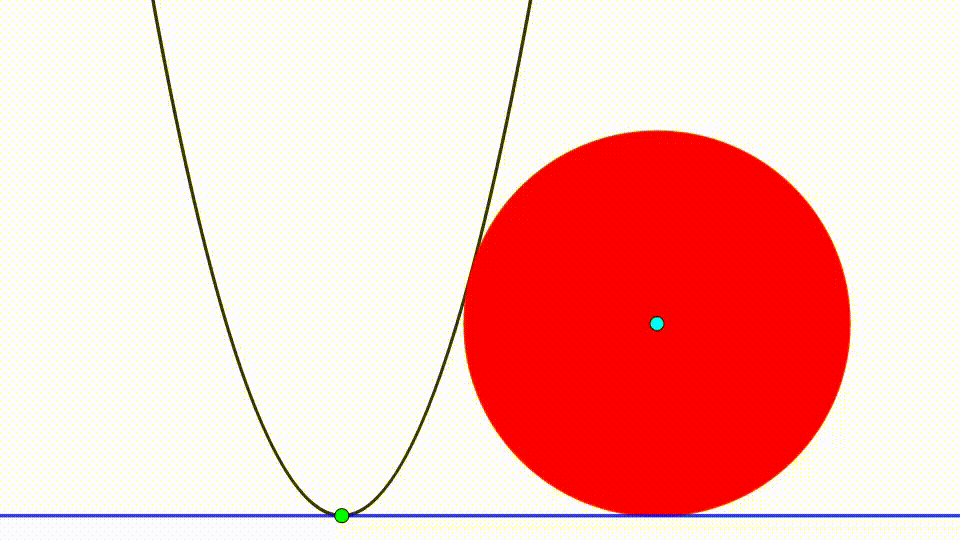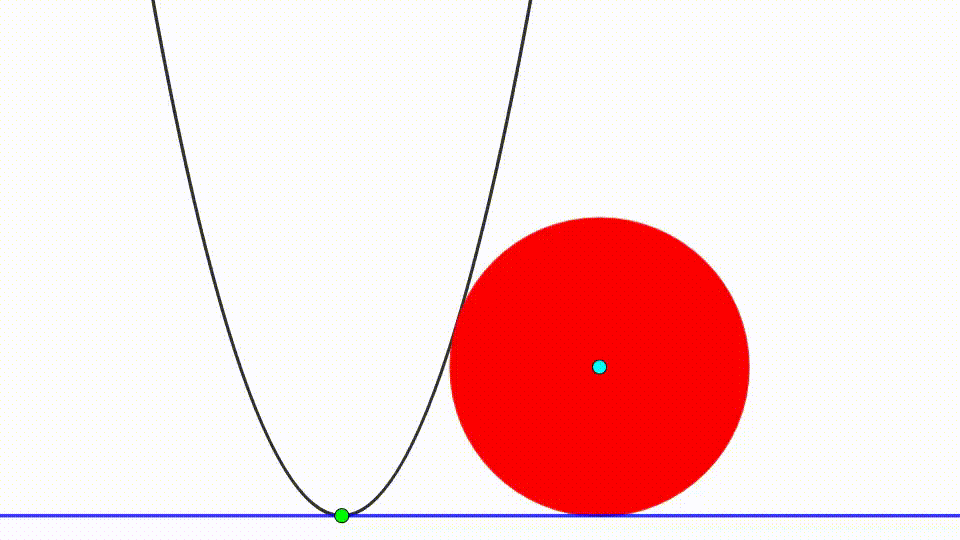 The diagram shows a black parabola
y
=
x
2
and a red circle moving so that it's tangent to the parabola and to the blue line
y
=
0
. When the ratio of the
x
-coordinate to the
y
-coordinate of the circle's center is equal to
5
3
6
, the square of the distance between the circle's center (cyan) and the origin (green) is an integer. What is this integer?
The diagram shows a black parabola
y
=
x
2
and a red circle moving so that it's tangent to the parabola and to the blue line
y
=
0
. When the ratio of the
x
-coordinate to the
y
-coordinate of the circle's center is equal to
5
3
6
, the square of the distance between the circle's center (cyan) and the origin (green) is an integer. What is this integer?
The answer is 79.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Nice solution !
Log in to reply
Thank you! You make nice animations, may I ask what tooling you use?
Log in to reply
Thanks ! Sure, I use geogebra geometry (with a parameter) to construct the figure. When I'm satisfied with the looks of the figure I use icecream recorder to record a video and i convert it to a gif file and voila !
One way to simplify the equation: let a = 4 y + 1 .
Log in to reply
Yes, that makes it look simpler, but how does it actually help solve the equation?
Log in to reply
I tried it, it simplifies indeed: you get 2 9 a 3 − 1 2 9 a 2 − 7 5 a − 2 5 = 0 which has one real solution: a = 5
It helps, rearranging the equation into a cubic function (which has an annoyingly long formula to find its roots).
Log in to reply
@Jeff Giff – This may be interesting to you: Mathologer on the cubic formula
... or just factoring out a − 5 by long division: ( a − 5 ) ( 2 9 a 2 + 1 6 a + 5 ) = 0 so solutions are a = 5 or a = 2 9 − 8 ± 9 i
BTW, on the ninth line(including the latex), you made a typo: 3 6
Let the point where the circle touches the parabola be ( x , y ) , then the tangent line at that point has slope 2 x . tan θ = 2 x Because y = x 2 and using trig identities: tan 2 θ = 4 y , cos 2 θ = 4 y + 1 1 , sin 2 θ = 4 y + 1 4 y If the circle has radius r, its centre is at C = ( x + r sin θ , r ) Also y = r + r cos θ ⇒ r y = 1 + 4 y + 1 1
Because y c x c = 5 3 6 r x + sin θ = 5 3 6 ⇒ r 2 x 2 + 2 r x sin θ + sin 2 θ = 2 5 5 4 ⇒ 2 r x sin θ = 2 5 5 4 − 4 y + 1 4 y − r 2 y ⇒ 4 r 2 x 2 sin 2 θ = ( 2 5 5 4 − 4 y + 1 4 y − r 2 y ) 2 ⇒ 4 r 2 y 4 y + 1 4 y = 4 y + 1 1 6 r 2 y 2 = ( 2 5 5 4 − 4 y + 1 4 y − r 2 y ) 2 Eliminating r using the expression for r y : ⇒ 4 y + 1 1 6 ( 1 + 4 y + 1 1 ) 2 = ( 2 5 5 4 − 4 y + 1 4 y − y 1 ( 1 + 4 y + 1 1 ) 2 ) 2 Now we have an equaltion with only one variable. Taking the root again and massaging a bit ⇒ y + 4 1 1 + 4 y + 1 = 2 5 5 4 − 4 y + 1 4 y − y 1 ( 1 + 4 y + 1 1 ) 2
Not clear how this simplifies or solves analytically, but trying y = 6 satisfies the equation and from there: r = 5
We need the value of d 2 = x c 2 + y c 2 = ( 5 3 6 r ) 2 + r 2 = 2 5 5 4 + 2 5 r 2 = 7 9