Dynamic Geometry: P100
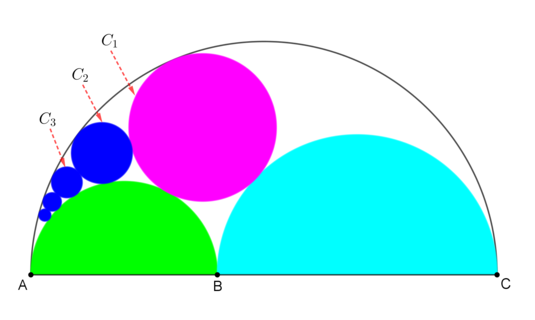
 The diagram shows a black semicircle with radius
1
. A red point moves freely on its diameter, creating two semicircles: cyan and green. The purple circle is internally tangent to the black semicircle and tangent to both cyan and green semicircles. There is an infinite number of blue circles. They are tangent to each other, internally tangent to the black semicircle and tangent to the green semicircle. There is an infinite number of yellow circles. They are tangent to each other, internally tangent to the black semicircle and tangent to the cyan semicircle. When the ratio of the radius of the
2
5
th blue circle to the radius of the
2
0
th yellow circle is equal to
6
0
9
4
1
7
7
9
, the ratio of the green semicircle's radius to the radius of the cyan semicircle can be expressed as
q
p
, where
p
and
q
are coprime positive integers. Find
p
+
q
.
The diagram shows a black semicircle with radius
1
. A red point moves freely on its diameter, creating two semicircles: cyan and green. The purple circle is internally tangent to the black semicircle and tangent to both cyan and green semicircles. There is an infinite number of blue circles. They are tangent to each other, internally tangent to the black semicircle and tangent to the green semicircle. There is an infinite number of yellow circles. They are tangent to each other, internally tangent to the black semicircle and tangent to the cyan semicircle. When the ratio of the radius of the
2
5
th blue circle to the radius of the
2
0
th yellow circle is equal to
6
0
9
4
1
7
7
9
, the ratio of the green semicircle's radius to the radius of the cyan semicircle can be expressed as
q
p
, where
p
and
q
are coprime positive integers. Find
p
+
q
.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
You made it very simple. Nice work.
Log in to reply
It was quite impossible using Descarte's theorem. I was surprised I solved it. I was trying to solve it numerically and saw the pattern. Once again, nice problem.
Log in to reply
Thank you sir. I calculated the First 6 radii of each kind of circles and by recurrence deducted a general formula for the nth radius.
Well I used brute force for solving this it took me a lot of time. Nice problem.
Log in to reply
aha I should have asked for the 100th radii ahah
Log in to reply
Yea by then I would been exhausted
Log in to reply
@Omek K – I will not stop at 100, I have more ideas...
One doubt only: in the third-last line, shouldn’t it be
k
1
>
1
?
(Since
0
<
k
1
1
<
1
) :)
 Let
A
B
,
B
C
be the diameters of the green and the cyan semicircles respectively.
Let
A
B
,
B
C
be the diameters of the green and the cyan semicircles respectively.
The sequence of the blue circles together with the purple circle form a Pappus chain { C 1 , C 2 , C 3 , … } . Using the ratio r = A C A B of the green and the black semicircles’ diameters, in which the chain is inscribed, the radius of the n t h circle of the chain is given by the expression: r n = 2 [ n 2 ( 1 − r ) 2 + r ] ( 1 − r ) r The 25th blue circle is the 26th circle of the chain, thus, its radius r b is r b = r 2 6 = 2 [ 2 6 2 ( 1 − r ) 2 + r ] ( 1 − r ) r Likewise, the set of the yellow circles together with the purple circle form a Pappus chain as well. The corresponding ratio of the diameters of the cyan and black semicircles of the arbelos is A C B C = A C A C − A B = 1 − r Using this ratio in the formula for the radii of the circles in the chain we get r n = 2 [ n 2 r 2 + ( 1 − r ) ] r ( 1 − r ) and for the radius of the 20th yellow circle we have r y = r 2 1 = 2 [ 2 1 2 r 2 + ( 1 − r ) ] r ( 1 − r ) According to the condition given in the problem we have the equation d 2 [ 2 1 2 r 2 + ( 1 − r ) ] r ( 1 − r ) 2 [ 2 6 2 r 2 + ( 1 − r ) ] r ( 1 − r ) = 6 0 9 4 1 7 7 9 ⇔ 2 6 2 r 2 + ( 1 − r ) 2 1 2 r 2 + ( 1 − r ) = 6 0 9 4 1 7 7 9 ⇔ 2 9 6 9 7 0 r 2 + 4 7 9 4 6 7 r − 2 3 9 3 0 2 = 0 ⇔ r > 0 r = 5 2 Consequently, the ratio of the green semicircle's radius to the radius of the cyan semicircle is r p u r p l e r g r e e n = B C A B = A C B C A C A B = 1 − r r = 1 − 5 2 5 2 = 3 2 For the answer, p = 2 , q = 3 , thus, p + q = 5 .
Very nice work Thanos !
Log in to reply
I'm glad you liked it. I had to upload a solution to celebrate your 100th Dynamic Geometry problem :) Keep it up.
So cool :)
Let the curvatures of the purple circle, green semicircle, and cyan semicircle be k 0 , k 1 , and k 2 respectively. This means that their radii are k 0 1 , k 1 1 , and k 2 1 respectively. By Descarte's theorem :
k 0 = k 1 + k 2 − 1 + 2 k 1 k 2 − k 1 − k 2 = k 1 + k 2 − 1 + 2 ( k 1 − 1 ) k 2 − k 1 = k 1 + k 2 − 1 + 2 k 1 − k 1 = k 1 + k 2 − 1
Let the curvatures of the n th blue circle and yellow circle be b n and y n respectively, and b 0 = y 0 = k 0 . Through observation it is found that
b n = ( k 1 − 1 ) ( n + 1 ) 2 + k 2
Let us prove this claim by induction for all n ≥ 0 .
When n = 0 , b 0 = k 1 − 1 + k 2 , Therefore the claim is true for n = 0 . Assuming that the claim is true for n , then
b n + 1 = b n + k 1 − 1 + 2 b n k 1 − b n − k 1 = ( k 1 − 1 ) ( n + 1 ) 2 + k 2 + k 1 − 1 + 2 ( k 1 − 1 ) b n − k 1 = ( k 1 − 1 ) ( ( n + 1 ) 2 + 1 ) + k 2 + 2 ( k 1 − 1 ) 2 ( n + 1 ) 2 + k 1 − k 1 = ( k 1 − 1 ) ( n 2 + 2 n + 2 ) + k 2 + 2 ( k 1 − 1 ) ( n + 1 ) = ( k 1 − 1 ) ( n 2 + 4 n + 4 ) + k 2 = ( k 1 − 1 ) ( n + 2 ) 2 + k 2
The claim is also true for n + 1 and it is true for all n ≥ 0 . Since k 1 and k 2 are interchangeable and k 0 is common,
y n = ( k 2 − 1 ) ( n + 1 ) 2 + k 1
When 1 / y 2 0 1 / b 2 5 = 6 0 9 4 1 7 7 9 , we have:
b 2 5 y 2 0 2 6 2 ( k 1 − 1 ) + k 2 2 1 2 ( k 2 − 1 ) + k 1 2 6 8 7 4 5 4 k 2 − 2 6 8 7 4 5 4 + 6 0 9 4 k 1 5 3 7 1 3 5 k 2 − 2 3 9 3 0 2 k 1 k 1 − 1 5 3 7 1 3 5 k 1 − 2 3 9 3 0 2 k 1 2 3 9 3 0 2 k 1 2 − 4 7 9 4 6 7 k 1 − 2 9 6 9 7 0 ( 2 k 1 − 5 ) ( 1 1 9 6 5 1 k 1 + 5 9 3 9 4 ) k 1 ⟹ 1 / k 2 1 / k 1 = 6 0 9 4 1 7 7 9 = 6 0 9 4 1 7 7 9 = 1 2 0 2 6 0 4 k 1 − 1 2 0 2 6 0 4 + 1 7 7 9 k 2 = 2 9 6 9 7 0 = 2 9 6 9 7 0 = 0 = 0 = 2 5 = k 1 k 2 = k 1 − 1 1 = 3 2 Note that k 1 1 + k 2 1 = 1 ⟹ k 2 = k 1 − 1 k 1 Since k 1 > 0
Therefore p + q = 2 + 3 = 5 .