Dynamic Geometry: P122

The equation of the green , purple line will be $-x^3+c$ , $x^3+c$ respectively.
Now, for first rectangle, let the coordinates of A will be ( $x_1 , -x^3_1 + c$ ).

So the area of 1st rectangle will be 2( $x_1$ )( $-x^3_1 + c$ ) let this be called a function f(x) for a given c. Therefore,

$\begin{aligned} f(x) &= 2(x)(-x^3 + c) \end{aligned}$

Now for area to be maximum

$\begin{aligned} {f}'(x) &= 0\\ 0 &= d(2(x)(-x^3 + c))\\ &= d(2(x)(-x^3 + c))\\ &= 2(-x^3+c) + 2(x)(-3x^2)\\ &= -8x^3 + 2c\\ 8x^3 &= 2c\\ x &= \sqrt[3]{\frac{c}{4}} \end{aligned}$

Therefore, $x_1$ = $\Large\sqrt[3]{\frac{c}{4}}$ at given c.

Now, consider second rectangle , let the coordinates of B will be ( $x_2 , -x^3_2 + c$ ).

So the area of 2nd rectangle will be 2( $x_2$ )( $-x^3_2 + c - (-x^3_1 + c)$ ) let this be called a function g(x) for a given c. Therefore,

$\begin{aligned} g(x) &= 2(x)(-x^3 + x^3_1) \end{aligned}$

Here $x^3_1$ is constant for a given c. Therefore we can repeat the same process and get $x_2$ = $\Large\sqrt[3]{\frac{x^3_1}{4}}$ = $\Large\sqrt[3]{\frac{c}{4^2}}$ .

In general, $x_n$ = $\Large\sqrt[3]{\frac{c}{4^n}}$ at given c for the nth rectangle.
In general, $y_n$ = - $\Large\frac{c}{4^n}$ + c

Now given, 2 $x_{12}$ ( $y_{12} - y_{11}$ ) = $\frac{3}{32768}$ = $\frac{3}{2^{15}}$ . Solve to get c as $2^{12}$ . (I am omitting the tedious work)
Required 4 $x_9$ + 2( $y_9 - y_8$ ) $\Rightarrow$ Substitute c to get the required value as $\frac{35}{32}$ .

Therefore
$\begin{aligned} \frac{p}{q} &= \frac{35}{32}\\ p+q &= 67 \end{aligned}$

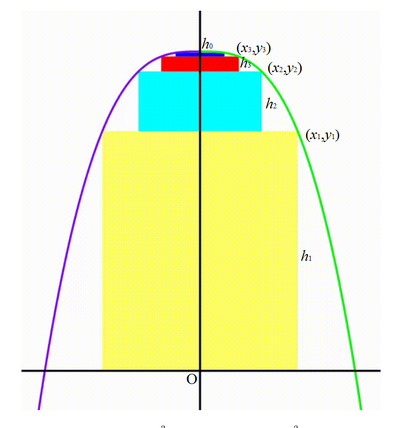
We note that the variable curve (purple and green curves combined) can be represented by $y = h_0 - |x^3|$ , where $h_0$ is the variable height of the curve. Since the curve is symmetrical about the $y$ -axis, we need only consider the positive quadrant. Let the height of the $n$ th maximum-area rectangle be $h_n$ and its top right vertex be $(x_n, y_n$ . Then we note that

$y_n = \sum_{k=1}^n h_k = h_0 - x_n^3$

First let us find the value of $h_1$ in terms of $h_0$ . The area of any inscribed rectangle is given by:

$\begin{aligned} A & = 2xy = 2x(h_0 - x^3) = 2h_0x - 2x^4 \\ \implies \frac {dA}{dx} & = 2h_0 - 8x^3 & \small \blue{\text{Putting }\frac {dA}{dx}=0} \\ x & = \sqrt[3]{\frac {h_0}4} \end{aligned}$

Since $\dfrac {d^2 A}{dx^2} < 0$ , $A$ is maximum, when $x = \sqrt[3]{\dfrac {h_0}4}$ . This means that $x_1 = \sqrt[3]{\dfrac {h_0}4}$ and $y_1 = h_0 - \dfrac {h_0}4 = \dfrac 34h_0$ . As $h_1 = y_1$ , $\implies h_1 = \dfrac 34 h_0$ . We note that the pattern repeats, and we have:

$\begin{array} {lll} h_1 = \dfrac 34 h_0 & y_1 = \dfrac 34 h_0 & x_1 = \sqrt[3]{h_0 - y_1} = \sqrt[3]{\dfrac {h_0}4} \\ h_2 = \dfrac 34 (h_0-y_1) = \dfrac {3h_0}{16} & y_2 = y_1 + h_2 = \dfrac {15}{16}h_0 & x_2 = \sqrt[3]{h_0 - y_2} = \sqrt[3]{\dfrac {h_0}{16}} \\ h_3 = \dfrac 34 (h_0-y_2) = \dfrac {3h_0}{64} & y_3 = y_2 + h_3 = \dfrac {63}{64}h_0 & x_3 = \sqrt[3]{h_0 - y_3} = \sqrt[3]{\dfrac {h_0}{64}} \\ \implies h_n = \dfrac {3h_0}{4^n} & y_n = \dfrac {4^n-1}{4^n} h_0 & x_n = \sqrt[3]{\dfrac {h_0}{4^n}} \end{array}$

The area of the $12$ th rectangle:

$\begin{aligned} A_{12} & = \frac 3{32768} = \frac 3{2^{15}} \\ 2x_{12}h_{12} & = \frac 3{2^{15}} \\ 2 \sqrt[3]{\frac {h_0}{4^{12}}} \cdot \frac {3h_0}{4^{12}} & = \frac 3{2^{15}} \\ \frac {h_0^\frac 43}{4^{16}} & = \frac 1{2^{16}} \\ h_0^\frac 43 & = 2^{16} \\ \implies h_0 & = 2^{12} = 4^6 \end{aligned}$

And the perimeter of the $9$ th rectangle:

$p_9 = 4x_9 + 2h_9 = 4 \cdot \sqrt[3]{\frac {4^6}{4^9}} + 2 \cdot \frac {3\cdot 4^6}{4^9} = 1+\frac 3{32} = \frac {35}{32}$

Therefore $p+q = 35+32 = \boxed{67}$ .