Dynamic Geometry: P23
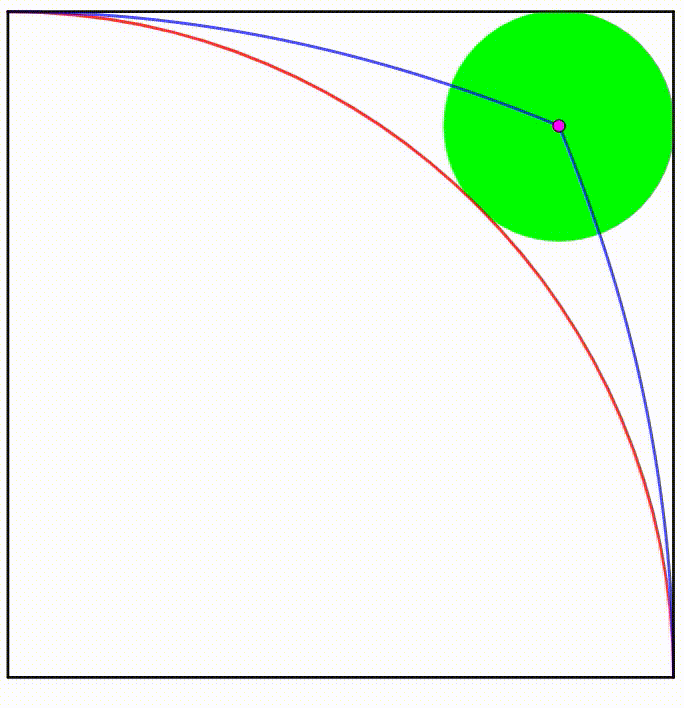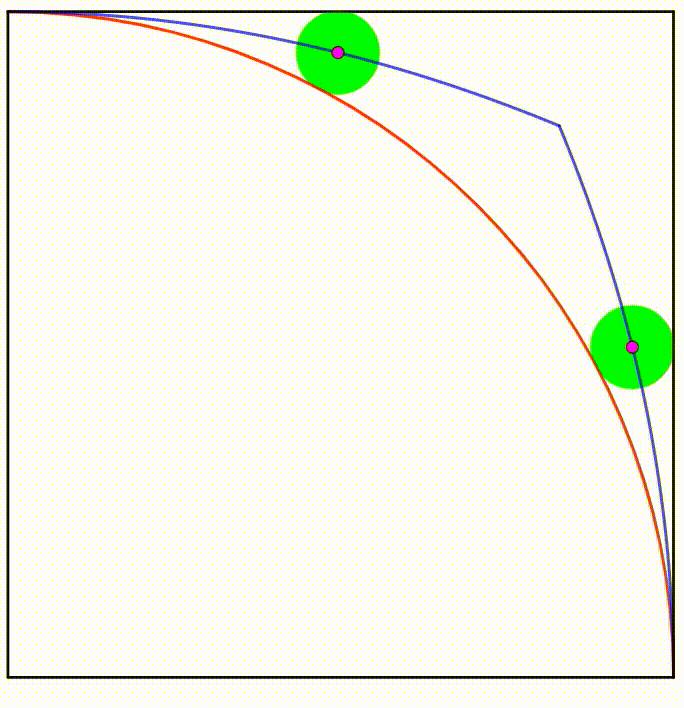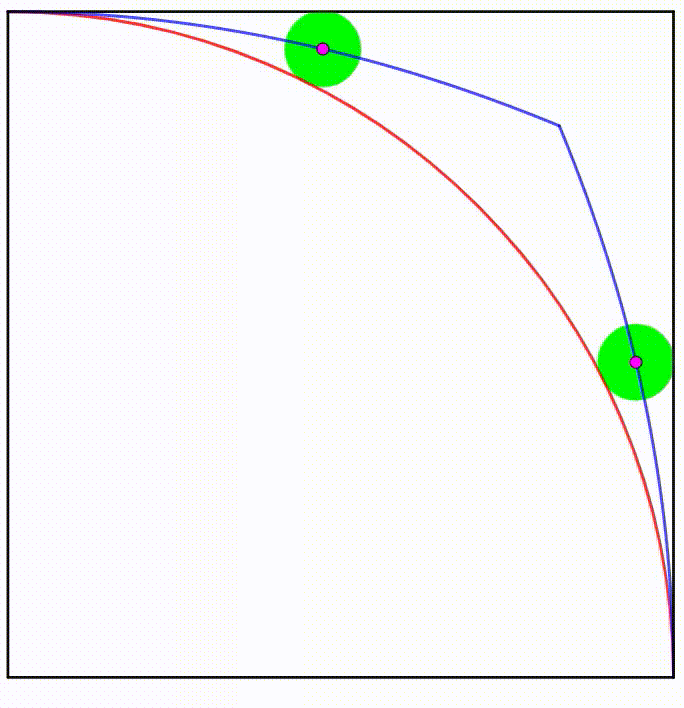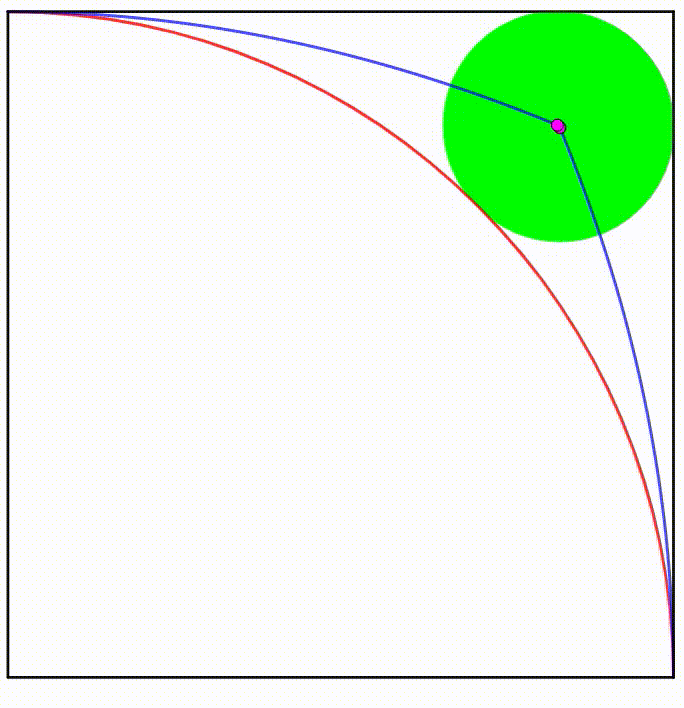
The diagram shows a unit square and a unit quadrant. The green circle is any circle which is always tangent to a side of the square and the quadrant. The centers of all such green circles trace a locus (blue curves).
The area bounded by the blue curves and the quadrant can be expressed as:
d a b − c − e π
where a , b , c , d , and e are positive integers, and b and d are primes. Find a + b + c + d + e + ⌈ π ⌉ .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Thank you for posting !
Log in to reply
You are welcome. I have edited the problem statement. Since there is only one square and one quadrant you don't need mention their color. Because nobody will be confused. Instead of of coprime and square-free we can fix the answer values using primes.
Log in to reply
Understood thank you !
Log in to reply
@Valentin Duringer – In geometry we talk about locus rather than moving. It is not a Mechanical Engineering problem. A moving object does not change in size. That was why I mentioned about variable circle. I have changed the problem statement again. Check if you understand,
You wrote: "By symmetry the right blue curve is given by" x 2 = 1 − 4 y 2 The square on x shouldn't be here (a typo, I guess). Nice solution nevertheless.
I did it the same way but I was lazy to do the integration, @Valentin Duringer I like your problems , please keep posting more
Log in to reply
Hi, im happy you like them. I have made 100 of them so I ll be posting more everyday !
Log in to reply
Thanks a lot !!
Log in to reply
@Om Krish – @OM Krish I'm posting right, enjoy and share ! Thanks !
Actually integration is unnecessary for parabola. I have updated the solution above.
Log in to reply
Sorry for the late reply I had actually changed accounts so I didn't see this , I like your solution sir
Let the bottom-left vertex of the square be the origin ( 0 , 0 ) of the x y -plane. Consider an arbitrary point P ( x , y ) on the top blue curve, where the radius of the circle is r . Then we note that x 2 + y 2 = ( 1 + r ) 2 . But we note that r = 1 − y . Then we have:
x 2 + y 2 x 2 ⟹ y = ( 1 + 1 − y ) 2 = y 2 − 4 y + 4 = 4 − 4 y = 1 − 4 x 2
By symmetry, the right blue curve is given by x = 1 − 4 y 2 . The two curves meet at y = x or
x x 2 + 4 x − 4 x 2 + 4 x + 4 ( x + 2 ) 2 ⟹ x = 1 − 4 x 2 = 0 = 8 = 8 = 2 ( 2 − 1 )
The area bounded by the blue curves and the red quadrant A is equal to the area bounded by the blue curves and the axes minus the area of the quadrant. The area of bounded by the blue curves and the axes is 2 A 1 + A 2 . [ U p d a t e d : ] Since y = 1 − 4 x 2 is a parabola, A 1 = 3 2 ( 1 − 2 ( 2 − 1 ) ) ( 2 ( 2 − 1 ) ) = 3 4 ( 5 2 − 7 ) . A 2 = ( 2 ( 2 − 1 ) ) 2 = 1 2 − 8 2 . Therefore A = 2 A 1 + A 2 − 4 π = 3 1 6 2 − 2 0 − 4 π . And the required answer is 7 .