Dynamic Geometry: P25
 The diagram shows a black semicircle with radius
1
. The cyan and the green semicircle are tangent to each other and internally tangent to the black semicircle. They are growing and shrinking freely so that the sum of their radius is always equal to
1
. We inscribe a yellow circle so that it's tangent to all three semicircles. The center of the yellow circle traces a
locus
(purple curve)
The area bounded by the purple curve and the diameter of the black semicircle can be expressed as:
The diagram shows a black semicircle with radius
1
. The cyan and the green semicircle are tangent to each other and internally tangent to the black semicircle. They are growing and shrinking freely so that the sum of their radius is always equal to
1
. We inscribe a yellow circle so that it's tangent to all three semicircles. The center of the yellow circle traces a
locus
(purple curve)
The area bounded by the purple curve and the diameter of the black semicircle can be expressed as:
d f π b − c
where f , b , c and d , are positive integers, and b is square-free. Find f + b + c + d .
The answer is 56.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Wait... don’t the ‘blue’ and ‘red’ circles all refer to the same yellow circle?
Log in to reply
Good to see yo ! Corrected. Thanks !
Log in to reply
@Jeff Giff Hello, Chew-Seong Cheong made two interesting notes about the series : https://brilliant.org/discussions/thread/about-dynamic-geometry-p80-85-90-95-99-105/?ref id=1615051 https://brilliant.org/discussions/thread/dynamic-geometry-p96-series/?ref id=1615329
Log in to reply
@Valentin Duringer – @Jeff Giff Sir Cheong also made this note : https://brilliant.org/discussions/thread/dynamic-geometry-p32-series/?ref_id=1615485
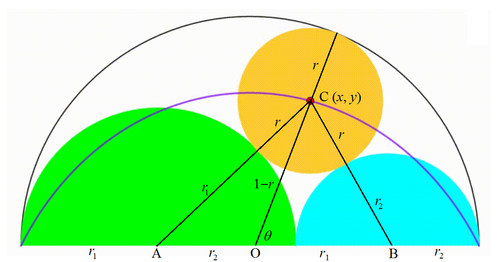
Let the centers of the large, green, and cyan semicircle, and the yellow circle be O , A , B , and C , and the radii of the green and cyan semicircles, and the yellow circle be r 1 , r 2 , and r respectively. Then r 1 + r 2 = 1 . Since A O = 1 − r 1 = r 2 and O B = 1 − r 2 = r 1 . By cosine rule ,
B C 2 ( r 2 + r ) 2 ( r 1 + r ) 2 = O B 2 + O C 2 − 2 ⋅ O B ⋅ O C ⋅ cos ∠ B O C = r 1 2 + ( 1 − r ) 2 − 2 r 1 ( 1 − r ) cos θ . . . ( 1 ) = r 2 2 + ( 1 − r ) 2 + 2 r 2 ( 1 − r ) cos θ . . . ( 2 ) Let ∠ B O C = θ . Similarly for C A 2
From r 2 ⋅ ( 1 ) + r 1 ⋅ ( 2 ) :
r 2 ( r 2 + r ) 2 + r 1 ( r 1 + r ) 2 r 1 3 + r 2 3 + 2 r ( r 1 2 + r 2 2 ) + ( r 1 + r 2 ) r 2 ( r 1 + r 2 ) ( ( r 1 + r 2 ) 2 − 3 r 1 r 2 ) + 2 r ( ( r 1 + r 2 ) 2 − 2 r 1 r 2 ) + r 2 1 − 3 r 1 r 2 + 2 r − 4 r 1 r 2 r + r 2 4 r − 4 r 1 r 2 r ⟹ r 1 r 2 = r 2 r 1 2 + r 1 r 2 2 + ( r 2 + r 1 ) ( 1 − r ) 2 = r 1 r 2 ( r 1 + r 2 ) + ( r 1 + r 2 ) ( 1 − 2 r + r 2 ) = r 1 r 2 + 1 − 2 r + r 2 = r 1 r 2 + 1 − 2 r + r 2 = 4 r 1 r 2 = 1 + r r Note that r 1 + r 2 = 1
To find what form the locus is, let O = ( 0 , 0 ) , the origin of the x y -plane, and an arbitrary point on the locus C = ( x , y ) . By Heron's formula , the area of △ A B C ,
A △ = ( r 1 + r 2 + r ) r 1 r 2 r = ( 1 + r ) ⋅ 1 + r r 2 = r Note that r 1 r 2 = 1 + r r
Since the base of △ A B C , A B = r 1 + r 2 = 1 , the height y = 2 r . By Pythagorean theorem ,
x 2 + y 2 x 2 + 4 3 y 2 + y x 2 + 4 3 ( y + 3 2 ) 2 3 4 x 2 + 9 1 6 ( y + 3 2 ) 2 = O C 2 = ( 1 − r ) 2 = 1 − 2 r + r 2 = 1 = 3 4 = 1 Note that y = 2 r
Therefore the locus is part of an ellipse with center at ( 0 , − 3 2 ) , minor-axis of length 3 2 , and major-axis 3 4 . Since it is an elliptical segment, we can find its area with geometrical means without using integration. The area under the locus is a 1 2 0 ∘ -elliptical segment and its area is given by:
A e = b a ( 3 π b 2 − 2 b 2 sin 1 2 0 ∘ ) = 2 3 ( 2 7 1 6 π − 9 4 3 ) = 2 7 8 3 π − 1 8
Therefore the required answer is 8 + 3 + 1 8 + 2 7 = 5 6 .
Well well well, thank you again maestro !
We shall use the Pythagorean theorem to express R ( a ) , x ( a ) and y ( a ) in terms of a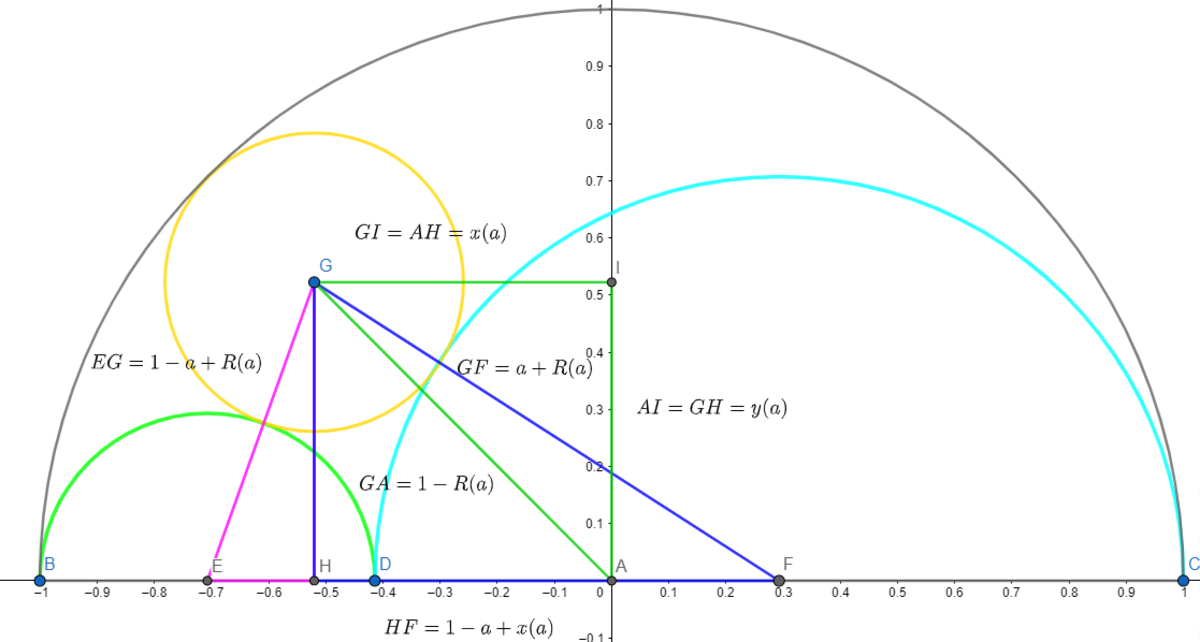
We shall write three equations using the diagram: