Dynamic Geometry: P37

Label the origin (cyan point) be $O(0,0)$ . Let the green point be $P(12k, 5k)$ , then the ratio of $y$ - to $x$ -coordinate is $\frac 5{12}$ and the distance $OP = 13k$ .

Let the center of the blue circle be $A \left(x_a, \frac 12\right)$ , the center of the pink circle be $B(0,r)$ , $C= \left(0, \frac 12\right)$ , and $D = \left(12k, \frac 12 \right)$ . Then $x_a = CA = \sqrt{AB^2-BC^2} = \sqrt{\left(r+\frac 12\right)^2-\left(r-\frac 12\right)^2} = \sqrt{2r}$ .

We note that $\triangle ABC$ and $\triangle APD$ are similar. Then we have:

$\begin{cases} \dfrac {CD}{CA} = \dfrac {PD}{AB} \implies \dfrac {12k}{\sqrt{2r}} = \dfrac r{r + \frac 12} \implies 6 k = \dfrac {r\sqrt{2r}}{2r+1} & ...(1) \\ \dfrac {PD}{BC} = \dfrac {AP}{AB} \implies \dfrac {5k-\frac 12}{r-\frac 12} = \dfrac {\frac 12}{r+\frac 12} \implies 5k = \dfrac {2r}{2r+1} & ...(2) \end{cases}$

$\implies \frac {(1)}{(2)}: \quad \sqrt{\frac r2} = \frac 65 \implies r = \frac {72}{25} \implies 5k = \frac {144}{169} \implies k = \frac {144}{845}$

Therefore, $OP = 13 k = \dfrac {144}{65}$ and $a+b = \boxed{209}$ .

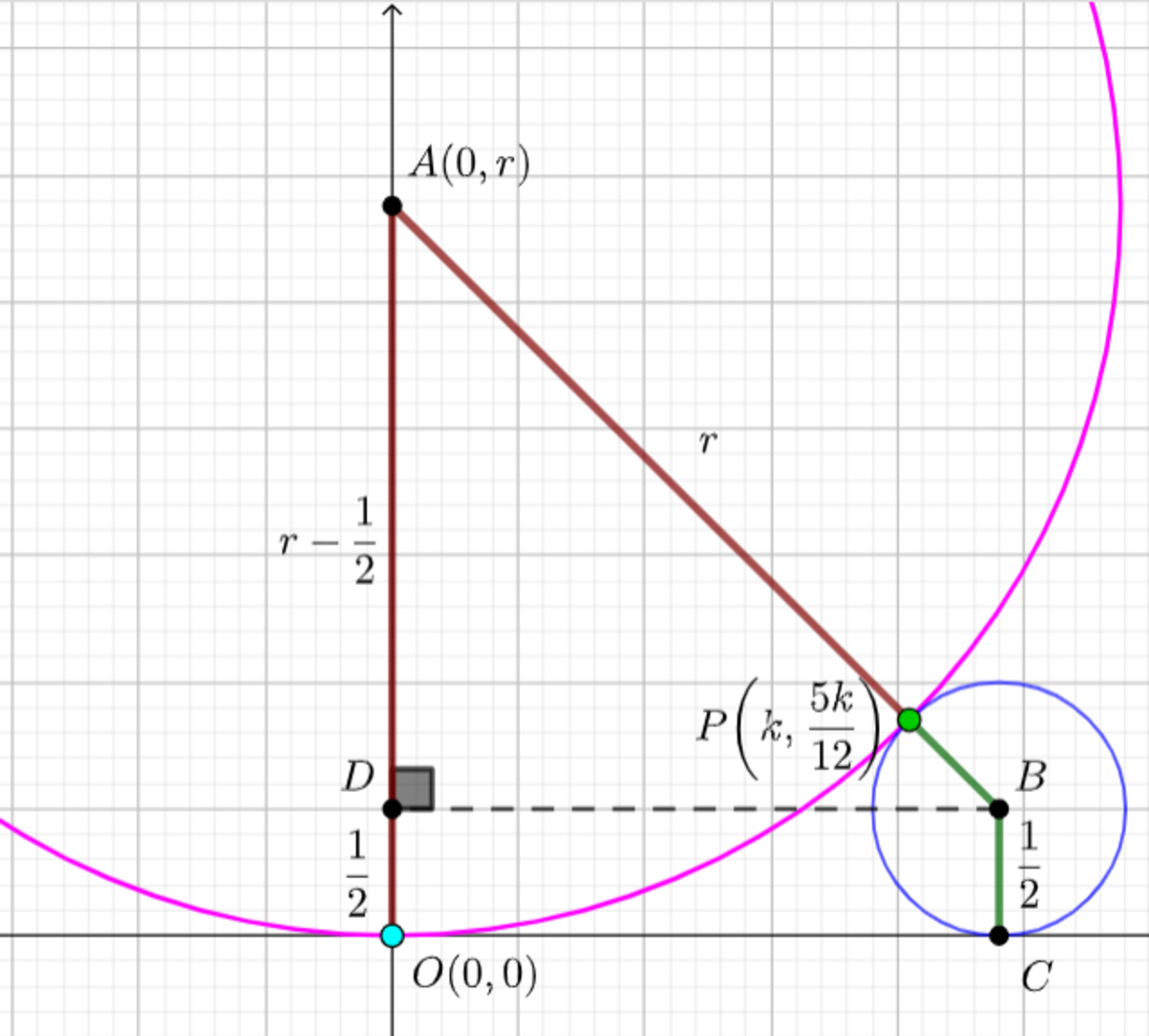
Define point $A$ as the center of the ${\color{#E81990}\text{pink}}$ circle, point $B$ as the center of the ${\color{#0C6AC7}\text{blue}}$ circle and $P$ is the common point.

In $\triangle ABD$ , $\begin{aligned} AB^2&=AD^2+BD^2\\ \left(r+\frac{1}{2}\right)^2&=\left(r-\frac{1}{2}\right)^2+BD^2 \\ BD^2&=\left(r+\frac{1}{2}\right)^2-\left(r-\frac{1}{2}\right)^2 \\ \implies BD&=\sqrt{2r} \end{aligned}$ So the above points have coordinates, $\begin{aligned} A&=(0,r) \\ B&=\left(\sqrt{2r},\frac{1}{2}\right) \\ P&=\left(k,\frac{5k}{12}\right) \\ O&=(0,0) \end{aligned}$ Note that $P$ divides line segment $AB$ into two parts, $AP=r$ and $BP=\dfrac{1}{2}$ . Using the section formula , $\begin{aligned} P&=\left(\frac{r\cdot \sqrt{2r}+\dfrac{1}{2}\cdot 0}{r+\dfrac{1}{2}},\; \frac{r\cdot \dfrac{1}{2}+\dfrac{1}{2}\cdot r}{r+\dfrac{1}{2}} \right ) \\ \\ \left(k,\frac{5k}{12}\right) &=\left(\frac{2r\sqrt{2r}}{2r+1},\; \frac{2r}{2r+1} \right) \\ \\ &\implies \begin{cases} k=\dfrac{2r\sqrt{2r}}{2r+1} \\ \\ \dfrac{5k}{12}=\dfrac{2r}{2r+1} \end{cases} \end{aligned}$ Solving the pair of equations, we have, $r=\dfrac{72}{25}$ and $k=\dfrac{1728}{845}$ . Distance between points $P$ and $O$ is, $\sqrt{k^2+\left(\frac{5k}{12}\right)^2}=\frac{13k}{12}=\frac{144}{65}$ $\therefore a=144,\; b=65 \implies a+b=\boxed{209}$