Dynamic Geometry: P47
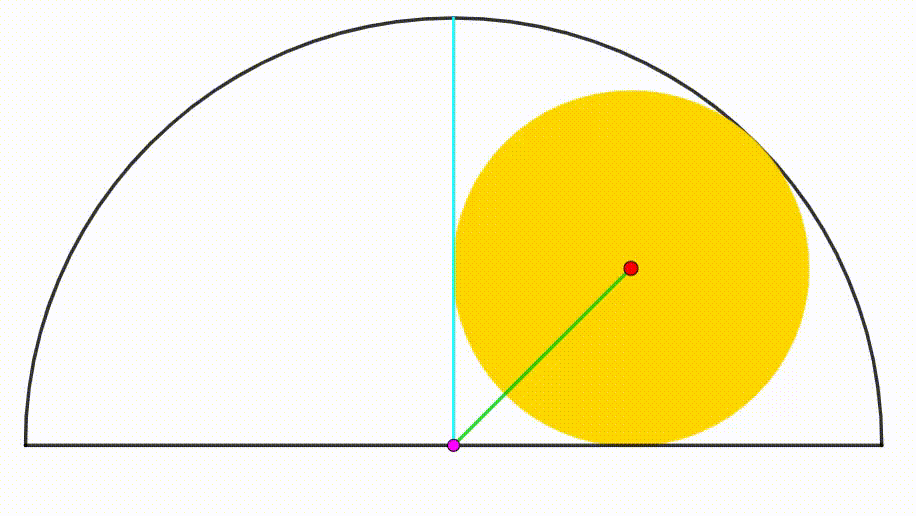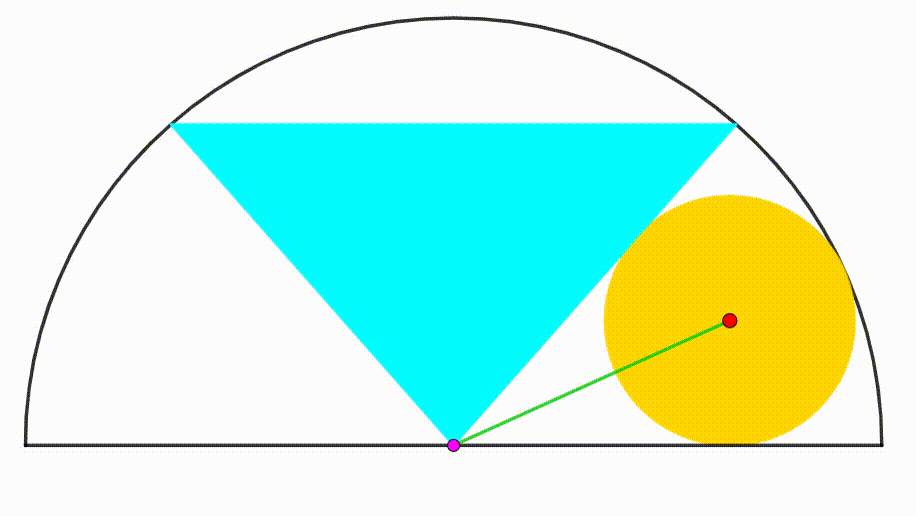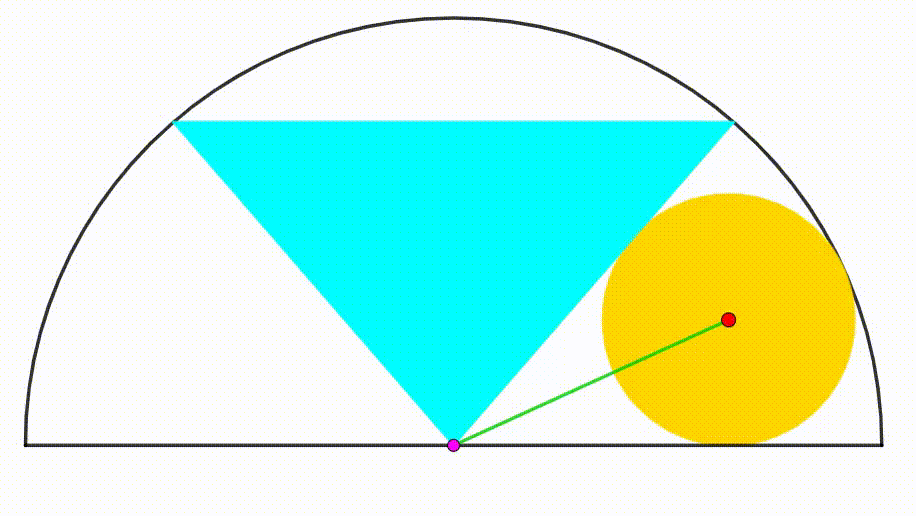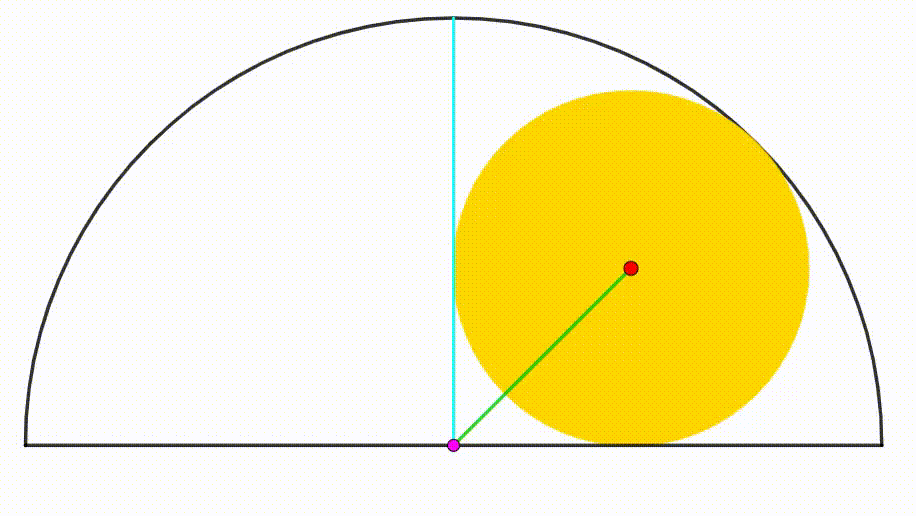 The diagram shows a semicircle with radius
1
. A isosceles triangle (cyan) is drawn such that the points of its base are moving symmetrically along the semicircle. The circle (yellow) is always internally tangent to the semicircle and to the triangle. When the product of the perimeter of the triangle and the circumference of the circle is equal to
4
9
6
6
π
, the distance between the center of the circle (red) and the center of the semicircle (pink) can be expressed as
q
p
for coprime positive integers
p
and
q
. Find
p
+
q
.
The diagram shows a semicircle with radius
1
. A isosceles triangle (cyan) is drawn such that the points of its base are moving symmetrically along the semicircle. The circle (yellow) is always internally tangent to the semicircle and to the triangle. When the product of the perimeter of the triangle and the circumference of the circle is equal to
4
9
6
6
π
, the distance between the center of the circle (red) and the center of the semicircle (pink) can be expressed as
q
p
for coprime positive integers
p
and
q
. Find
p
+
q
.
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Cool solution with angles, thank you for posting !
Why isn't r = 2 5 1 1 a valid solution?
Log in to reply
It exceeds the maximum possible value of r .
Log in to reply
Can you show this in your solution (along with how to find the maximum possible value of r)?
Log in to reply
@David Vreken – Done, I have made some changes.
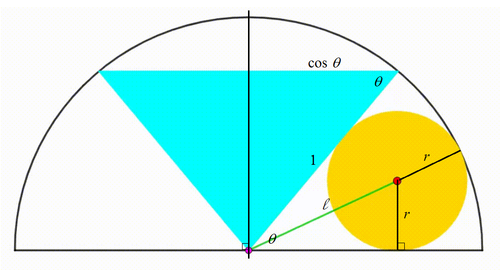
Let the distance between the centers of the circle and the semicircle be ℓ and the radius of the circle be r at an instant in time. Let the angle between a leg of the isosceles triangle and the diameter of the semicircle be θ . Note that the green line bisects the angle θ and
ℓ + r ℓ + ℓ sin 2 θ ⟹ sin 2 θ = 1 = 1 = ℓ 1 − ℓ
Now note that the perimeter of the triangle is p = 2 + 2 cos θ and the product of the circumference of the circle and the perimeter of the triangle is 2 π r p and when the product is equal to 4 9 6 6 π :
2 π ℓ sin 2 θ ( 2 + 2 cos θ ) 2 ℓ sin 2 θ ( 1 + 1 − 2 sin 2 2 θ ) ℓ 4 ℓ ( 1 − ℓ ) ( 1 − ( ℓ 1 − ℓ ) 2 ) 1 9 6 ( 1 − ℓ ) ( 2 ℓ − 1 ) 4 2 5 ℓ 2 − 5 8 8 ℓ + 1 9 6 ( 1 7 ℓ − 1 4 ) ( 2 5 ℓ − 1 4 ) ⟹ ℓ = 4 9 6 6 π = 4 9 3 3 = 4 9 3 3 = 3 3 ℓ 2 = 0 = 0 = 1 7 1 4 See note: ℓ = 2 5 1 4 is unacceptable.
Therefore p + q = 1 4 + 1 7 = 3 1 .
Note: For ℓ = 2 5 1 4 , the circle is tangent to the left leg of the isosceles triangle.
Therefore, ∣ O A ∣ = 1 − r = 1 7 1 4 ⟹ p + q = 3 1
Note: The quadratic equation, 4 2 5 r 2 − 2 6 2 r + 3 3 = 0 , yields two solutions, r 1 = 1 7 3 and r 2 = 2 5 1 1 . But r 2 must be discarded since 2 5 1 1 = r 2 > r max = 2 − 1 .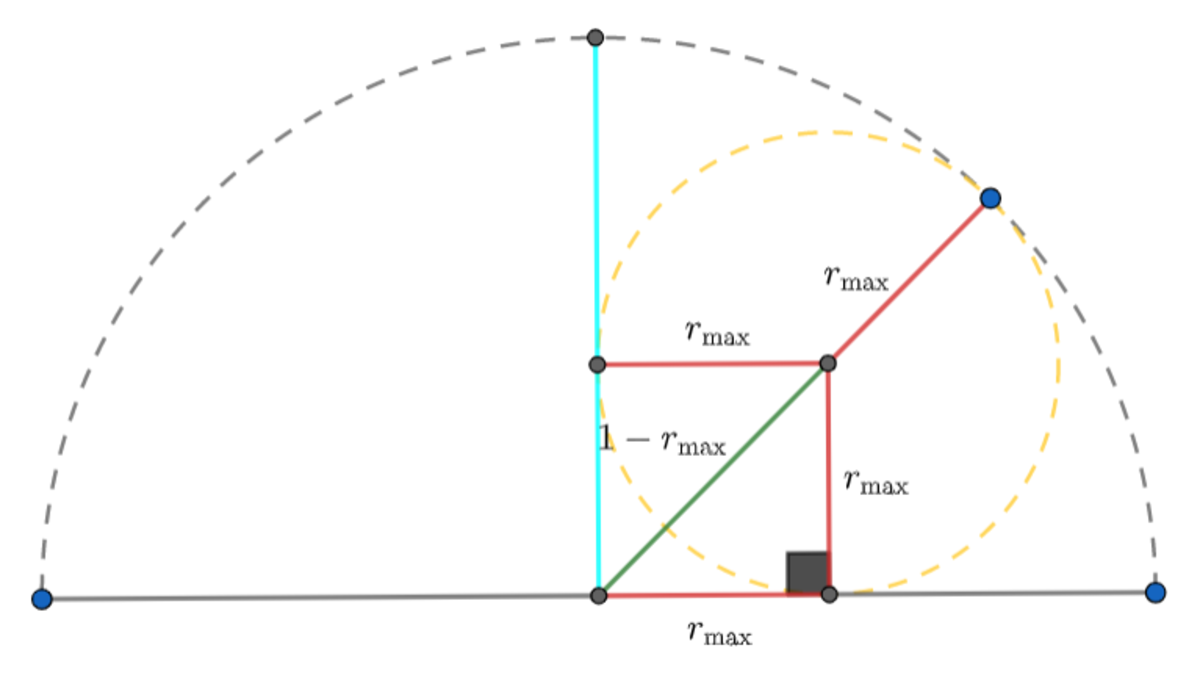 (
1
−
r
max
)
2
1
−
r
max
∴
r
max
=
r
max
2
+
r
max
2
=
r
max
2
=
2
+
1
1
=
2
−
1
(
1
−
r
max
)
2
1
−
r
max
∴
r
max
=
r
max
2
+
r
max
2
=
r
max
2
=
2
+
1
1
=
2
−
1