Dynamic Geometry: P66

Let $ABCD$ be the square. Denote the centers of the semicircles by $K$ , $L$ and their intersection point by $P$ . Let $\angle KDP=\angle KPD=θ$ and $\angle LBP=\angle LPB=φ$ .

Points $K$ , $P$ and $L$ are collinear, and $\angle AKL=2θ$ , $\angle ALK=2φ$ , thus $2\theta +2\varphi =180{}^\circ -\angle KAL=180{}^\circ -90{}^\circ =90{}^\circ$ , hence $\theta +\varphi =45{}^\circ$ From this we get that $\angle DPB=180{}^\circ -\left( \theta +\varphi \right) =180{}^\circ -45{}^\circ =135{}^\circ$ and this implies that $P$ lies on the circle with center $B$ and radius $CB=1$ , hence the pink curve is a quarter of this circle.

Finally, the area $A$ bounded by the red and the pink curve is $A={{A}_{\left( A,\overset\frown{BD} \right)}}+{{A}_{\left( C,\overset\frown{BD} \right)}}-\left[ ABCD \right]=\frac{\pi }{4}+\frac{\pi }{4}-1=\frac{\pi }{2}-1$ For the answer, $a=2$ , $b=-1$ , thus $a+b=\boxed{1}$ .

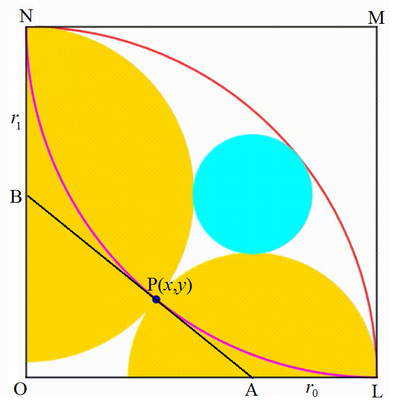
Label the unit square $LMNO$ , where $O(0,0)$ is the origin of the $xy$ -plane, the centers of the right and left semicircles be $A$ and $B$ respectively, and an arbitrary point on the locus be $P(x,y)$ . Let the radii of the two semicircles be $r_0$ and $r_1$ as shown. Then

$\begin{cases} A = (1-r_0, 0) \\ B = (0, 1-r_1) \end{cases} \implies P(x,y): \begin{cases} x = \dfrac {r_1(1-r_0)}{r_0+r_1} \\ y = \dfrac {r_0(1-r_1)}{r_0+r_1} \end{cases}$

By Pythagorean theorem ,

$\begin{aligned} OA^2 + OB^2 & = AB^2 \\ (1-r_0)^2 + (1-r_1)^2 & = (r_0+r_1)^2 \\ 1 - r_0 - r_1 & = r_0r_1 \\ \implies r_1 & = \frac {1-r_0}{1+r_0} \end{aligned}$

Now consider:

$\begin{aligned} (x-1)^2 + (y-1)^2 & = \left(\frac {r_1(1-r_0)}{r_0+r_1} - 1 \right)^2 + \left(\frac {r_0(1-r_1)}{r_0+r_1} - 1 \right)^2 \\ & = \left(\frac {-r_0(1+r_1)}{r_0+r_1} \right)^2 + \left(\frac {-r_1(1+r_0)}{r_0+r_1} \right)^2 \\ & = \frac {(2r_0)^2+(1-r_0^2)^2}{(1+r_0^2)^2} = \frac {4r_0^2+1-2r_0^2+r_0^4}{(1+r_0^2)^2} \\ & = \frac {(1+r_0^2)^2}{(1+r_0^2)^2} = 1 \end{aligned}$

This means that the locus is circular quadrant with center $(1,1)$ and radius $1$ . Therefore the area bounded by the red quadrant and the locus is twice the area of a $90^\circ$ circular segment with radius $1$ or

$2 \left(\frac \pi 4 - \frac 12 \right) = \frac \pi 2 - 1$

Therefore $a+b = 2-1 = \boxed 1$ .