Dynamic Geometry: P92
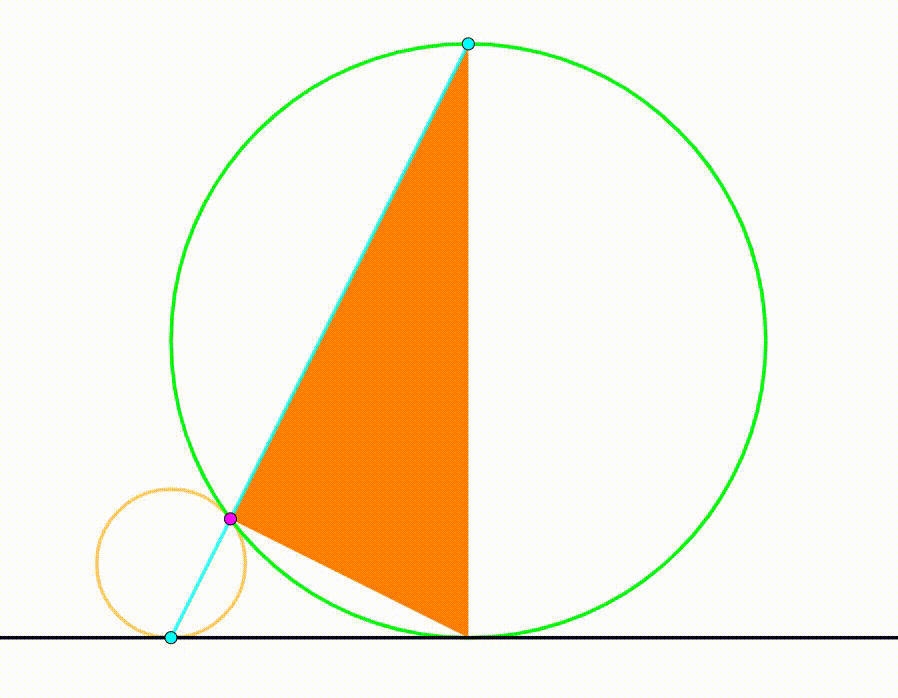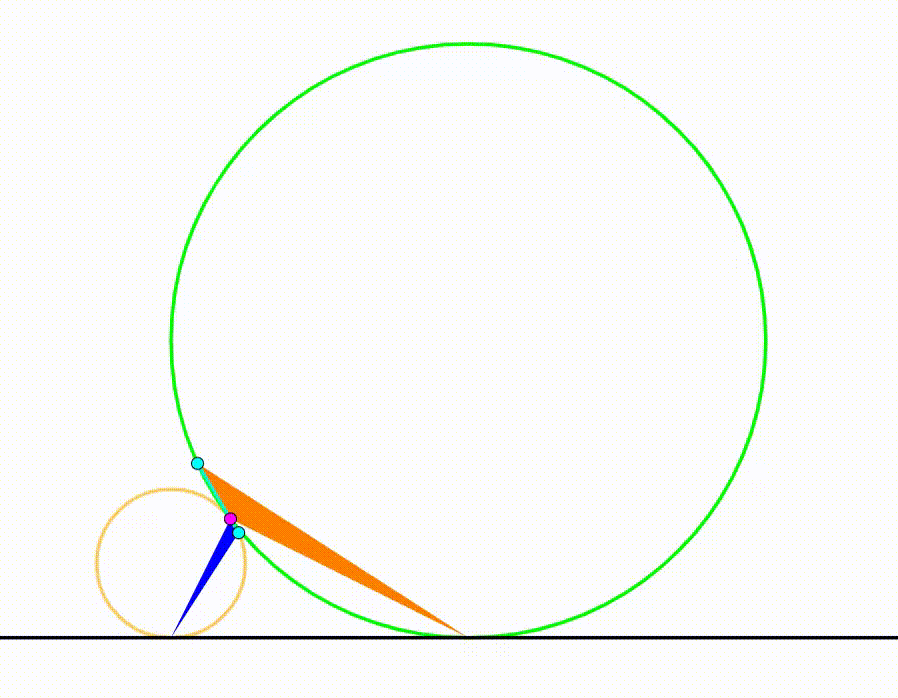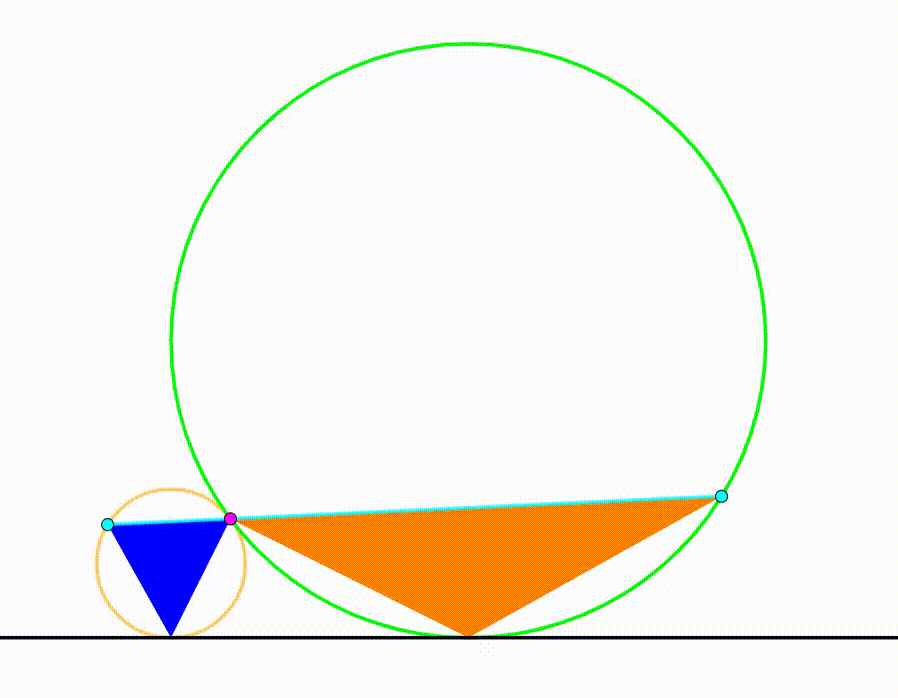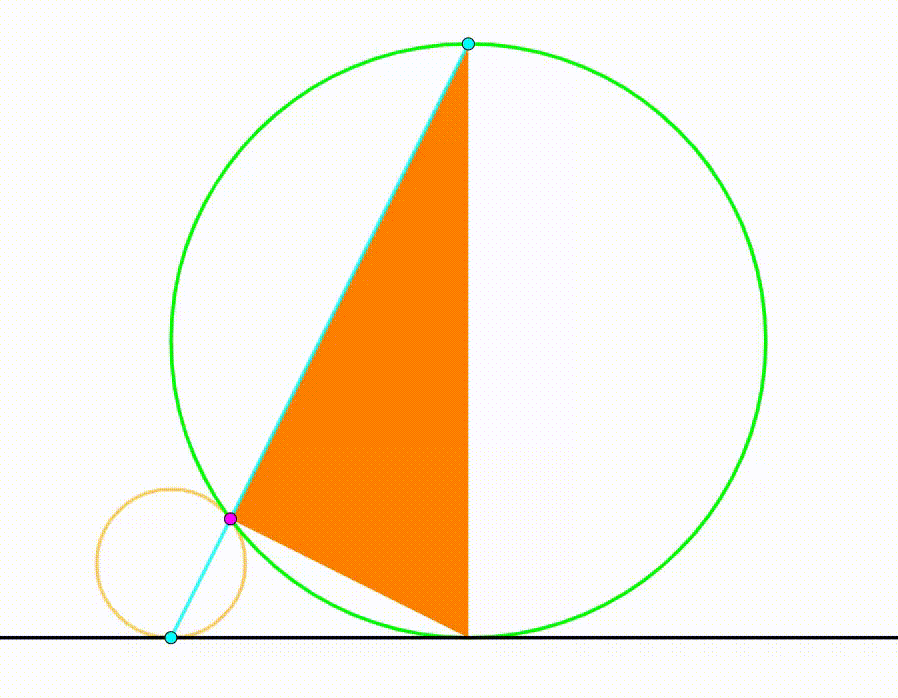 The diagram shows a yellow circle with radius
1
and a green circle with radius
4
. They are tangent to each other and tangent to the same black horizontal line. The purple point is their tangency point. The cyan line passes through this point and rotates freely so that we can draw two triangles (blue and orange) using the purple tangency point, the tangency point between the circles and the black horizontal line and the intersection points between the cyan line and both circles. When the sum of the areas of the triangles is
maximum
, the ratio of the blue triangle's area to the area of the orange triangle can be expressed as:
The diagram shows a yellow circle with radius
1
and a green circle with radius
4
. They are tangent to each other and tangent to the same black horizontal line. The purple point is their tangency point. The cyan line passes through this point and rotates freely so that we can draw two triangles (blue and orange) using the purple tangency point, the tangency point between the circles and the black horizontal line and the intersection points between the cyan line and both circles. When the sum of the areas of the triangles is
maximum
, the ratio of the blue triangle's area to the area of the orange triangle can be expressed as:
m p − q
where p , q and m are coprime positive integers, and p is square-free. Find 5 p + q + m .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Great solution!
Log in to reply
Nice problem.
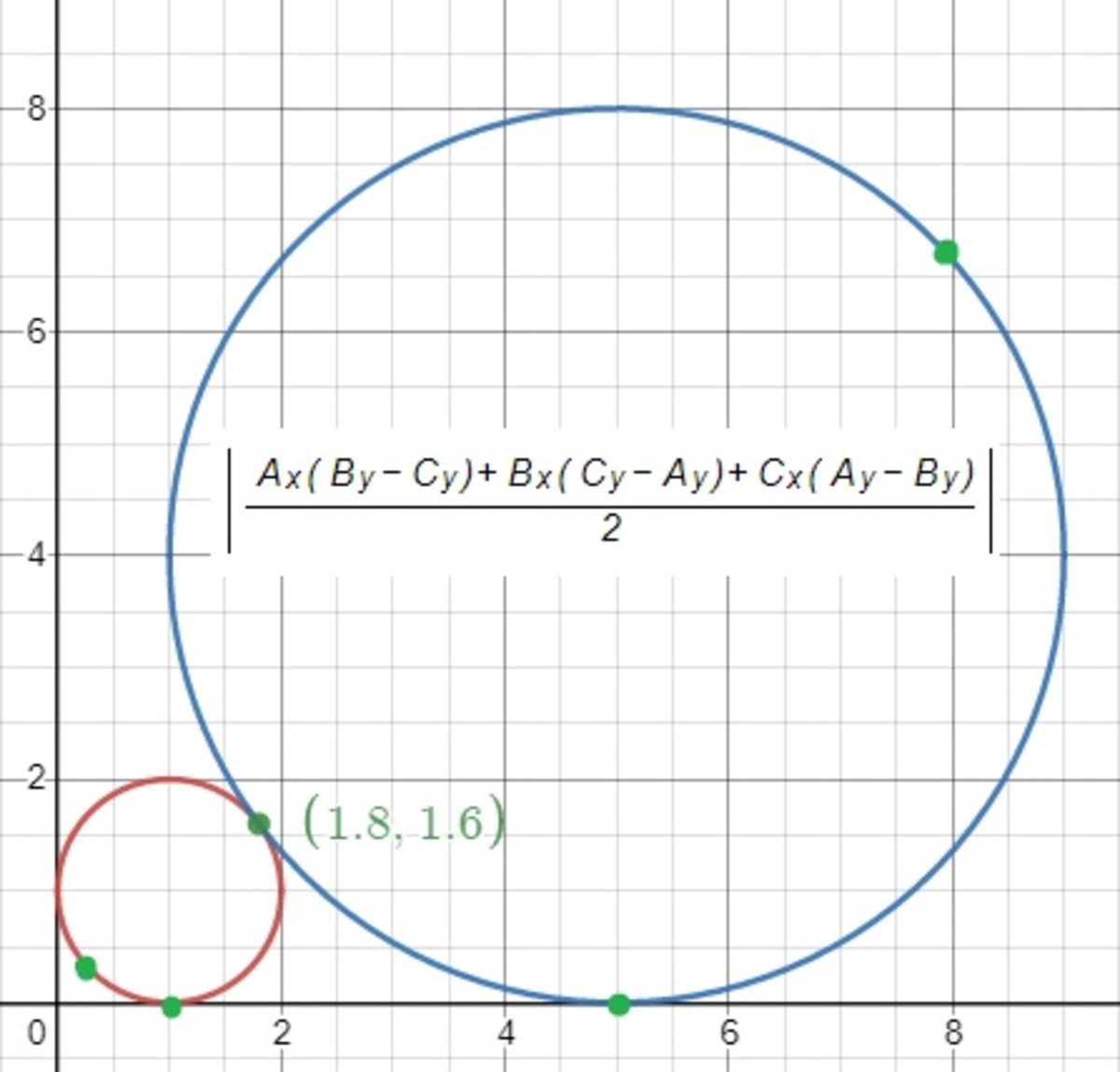 We start by positioning the circles. The smaller is tangent to the y axis with center at (1,1) and the bigger circle is tangent to the smaller with center at (5,4)
We start by positioning the circles. The smaller is tangent to the y axis with center at (1,1) and the bigger circle is tangent to the smaller with center at (5,4)
Equating ( x − 1 ) 2 + ( y − 1 ) 2 = 1 and ( x − 5 ) 2 + ( y − 4 ) 2 = 1 6 , gives point ( 5 9 , 5 8 ) as intersection.
Now we have 2 fixed points for each triangle, the intersection point and the points where the circles are tangent to the x axis, (1,0) and (5,0).
Looking at the bigger circle, the third point needed to use the area formula is just ( x , f ( x ) ) . We use the top semi-circle because it will create a bigger triangle, so f ( x ) = − ( x − 9 ) ( x − 1 ) + 4 . For the smaller circle, we need a point that can be mapped from the other that is traveling around the bigger circle.
| x 2 | x |
| 0 | 9 |
| 1 | 5 |
| 2 | 1 |
x = − 4 x 2 + 9 ⟹ x 2 = 4 9 − x
We insert this modified x into the bottom semi-circle function to get point ( x 2 , f ( x 2 ) ) with f ( x 2 ) = 1 − 4 ( 1 − x ) ( x − 9 )
After plugging these points into the formula provided at the top, we get the equations for the area of both triangles as a function of x . Long story short:

https://www.desmos.com/calculator/i1h9vjd2hn made this although useless when answering this question
Log in to reply
Visual tools are essential for me, they always provide major clues. You made a small mistake however, see if you can spot it.
Log in to reply
tell me, thanks
Log in to reply
@Jonathan Xiang – One of your fixed distances "D" has an error.
Let the large and small triangles be A B C and C D E respectively, where B , C , and D are fixed tangent points of the two circles with the base line and with each other; S T through C be parallel to B D , C N be perpendicular to B D : and the centers of the small and large circles be O and P respectively.
We note that O C = O D = 1 and the tangent of O P is 4 3 . Then D N = 5 4 , C N = 1 + 5 3 = 5 8 , by Pythagorean theorem , C D = C N 2 + D N 2 = 5 4 , B N = B D − D N = 4 − 5 4 = 5 1 6 , and B C = B N 2 + C N 2 = 5 8 .
The area of △ A B C is given by:
[ A B C ] = 2 1 ⋅ C A ⋅ B C ⋅ sin ∠ A C B = 2 1 ⋅ 2 ⋅ C P ⋅ cos ∠ P C A ⋅ B C ⋅ sin ∠ A C B = C P ⋅ B C ⋅ cos ( ∠ P C T − ∠ A C T ) sin ( ∠ A C T + B C T ) = 5 3 2 cos ( tan − 1 4 3 − θ ) sin ( θ + tan − 1 2 1 ) = 5 3 2 ( 5 3 sin θ + 5 4 cos θ ) ( 5 2 sin θ + 5 1 cos θ ) = 2 5 3 2 ( 3 sin θ + 4 cos θ ) ( 2 sin θ + cos θ ) = 2 5 3 2 ( 6 sin 2 θ + 1 1 sin θ cos θ + 4 cos 2 θ ) Let ∠ A C T = θ
Similarly,
[ C D E ] = 5 4 cos ( tan − 1 4 3 − θ ) sin ( tan − 1 2 − θ ) = 2 5 4 ( − 3 sin 2 θ + 2 sin θ cos θ + 8 cos θ )
Then the sum of areas of the two triangles:
S = [ A B C ] + [ B C D ] = 5 4 ( 9 sin 2 θ + 1 8 sin θ cos θ + 8 cos 2 θ ) = 5 2 ( 1 8 sin 2 θ + 3 6 sin θ cos θ + 1 6 cos 2 θ ) = 5 2 ( sin 2 θ − c o s 2 θ + 3 6 sin θ cos θ + 1 7 ) = 5 2 ( 1 8 sin 2 θ − cos 2 θ + 1 7 ) = 5 2 ( 5 1 3 cos ( 2 θ − tan − 1 1 8 1 ) + 1 7 )
Therefore S is maximum when 2 θ − tan − 1 1 8 1 = 2 π ⟹ θ = 4 π + 2 1 tan − 1 1 8 1 . Then the ratio of
[ A B C ] [ C D E ] = 5 3 2 cos ( tan − 1 4 3 − θ ) sin ( θ + tan − 1 2 1 ) 5 4 cos ( tan − 1 4 3 − θ ) sin ( tan − 1 2 − θ ) = 8 sin ( θ + tan − 1 2 1 ) sin ( tan − 1 2 − θ ) = 8 2 6 1 ( 1 3 + 3 1 3 2 6 1 ( 1 3 − 3 1 3 = 1 6 1 3 1 3 − 3 1 3 = 1 6 1 3 − 3
Therefore 5 p + q + m = 5 1 3 + 3 + 1 6 = 2 .