Dynamics of Constrained Charged Particles

As it is not mentioned, we assume that there is no gravity.

Since there is no external force acting on the system along the $Y$ -direction, linear momentum of the system remains conserved along this direction. At the instant the charges are the closest, there is no motion of them along the $X$ -direction, and since the rods are rigid, their speeds along the $Y$ -direction are equal, and equal to that of the uncharged particle. Let the required minimum seperation be $x$ and the velocity at that instant of each particle along the $Y$ -direction be $V$ . Then the linear momentum conservation equation yields

$m_0v=(m_0+2m)V$

$\implies V=\dfrac {m_0v}{m_0+2m}$

Energy conservation equation yields

$\dfrac {1}{2}m_0v^2+\dfrac{Q^2}{8π\epsilon_0L}$

$=\dfrac{1}{2}(m_0+2m)V^2+\dfrac{Q^2}{4π\epsilon_0x}$

$\implies \dfrac{Q^2}{4π\epsilon_0x}$

$=\dfrac{m_0mv^2}{m_0+2m}+\dfrac{Q^2}{8π\epsilon_0L}$

Substituting values we get

$\dfrac{1}{x}=\dfrac{1}{4}+\dfrac{2\times \frac{1}{2}}{4}=\dfrac{3}{8}$

$\implies x=\dfrac{8}{3}\approx \boxed {2.6667}$ .

Fun problem. Let $\theta$ be the angle of the rod below the horizontal. Let $y_0$ be the vertical position of the middle ball. The position and velocity of the ball on the right are:

$x = L \cos \theta \\ y = y_0 - L \sin \theta \\ \dot{x} = -L \sin \theta \dot{\theta} \\ \dot{y} = \dot{y}_0 - L \cos \theta \dot{\theta}$

Since $\dot{x}$ and $\dot{y}$ are zero in the beginning, and $\theta = 0$ as well, we know that $\dot{\theta} = \frac{v}{L}$ in the beginning. The kinetic energy, potential energy, and Lagrangian are:

$T = m L^2 \dot{\theta}^2 + m \dot{y_0}^2 - 2 m L \cos \theta \dot{\theta} \dot{y_0} + \frac{1}{2} m_0 \dot{y_0}^2 \\ V = \frac{k q^2}{2 L \cos \theta} \\ \mathcal{L} = T - V = m L^2 \dot{\theta}^2 + m \dot{y_0}^2 - 2 m L \cos \theta \dot{\theta} \dot{y_0} + \frac{1}{2} m_0 \dot{y_0}^2 - \frac{k q^2}{2 L \cos \theta}$

Equations of motion:

$\frac{d}{dt} \frac{\partial{\mathcal{L}}}{\partial{\dot{y_0}}} = \frac{\partial{\mathcal{L}}}{\partial{y_0}} \\ \frac{d}{dt} \frac{\partial{\mathcal{L}}}{\partial{\dot{\theta}}} = \frac{\partial{\mathcal{L}}}{\partial{\theta}}$

Crunching out the math results in the following coupled linear system:

\[\begin{pmatrix} 2m + m_0 & -2 m L \cos \theta \\ -2 m L \cos \theta & 2 m L^2 \\

\end{pmatrix}

\begin{pmatrix} \ddot{y}_0 \\ \ddot{\theta} \\

\end{pmatrix} = \begin{pmatrix} -2 m L \sin \theta \, \dot{\theta}^2 \\ -\frac{k q^2}{2L} \sec \theta \tan \theta \\

\end{pmatrix} \]

Initialize variables appropriately and solve the linear system for the double-dot terms on every time step. Numerical integration yields a minimum distance $D_{min} \approx 2.6667$ between the balls on the side. Note that while there may be simpler solutions to this particular problem based on energy conservation, this approach allows examination of other aspects of the dynamics.

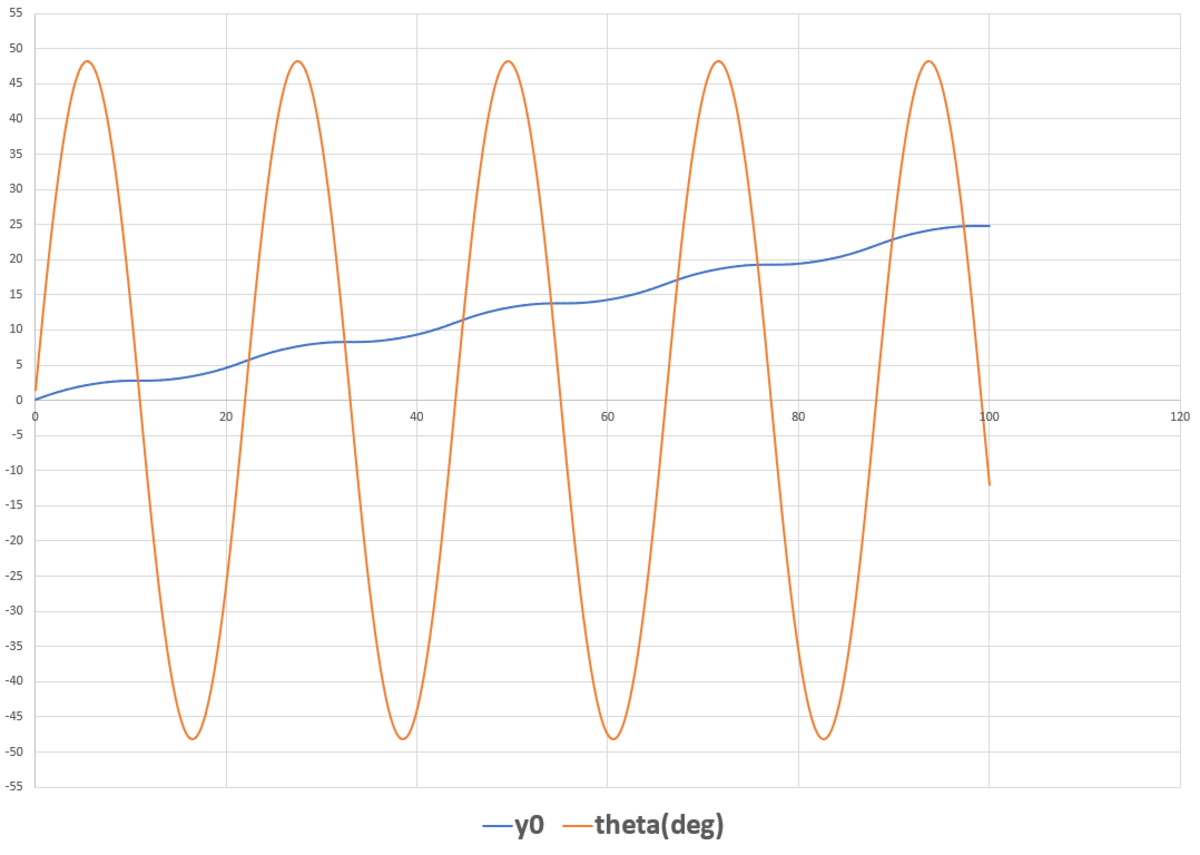
The plot below shows $y_0$ and $\theta$ (in degrees) over time from $t = 0$ to $t = 100$ . You can see that $\theta$ oscillates sinusoidally, while $y_0$ increases steadily with some small oscillation on top.