Convex Quadratic?
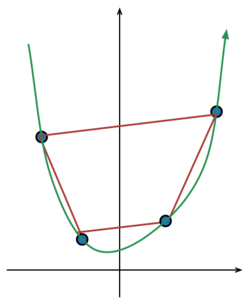 Consider a curve
y
=
a
x
2
+
b
x
+
c
with
a
,
b
,
c
∈
N
which passes through four points
A
(
−
2
,
3
)
,
B
(
−
1
,
1
)
,
C
(
α
,
β
)
,
D
(
2
,
7
)
.
Consider a curve
y
=
a
x
2
+
b
x
+
c
with
a
,
b
,
c
∈
N
which passes through four points
A
(
−
2
,
3
)
,
B
(
−
1
,
1
)
,
C
(
α
,
β
)
,
D
(
2
,
7
)
.
All these points are taken in given order for constructing a convex quadrilateral, which has maximum possible area.
Find minimum possible value of a + b + c + 2 α + 4 β .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Log in to reply
This is the way ,I had killed it while solving , Even My freind do not agree in this claim. So I just posted this and expecting this solution ! Good job bro ! +1 :)
Amazing solution and that AM part was awesome.
Love the last part ! Its like playing around the wicket.
What is the use of convex quadrilateral ?
what about alpha = 0 and betha = 1?
That is way better than my method ! Thanks !
A very nice solutions! Thanks
We get the eq y = x 2 + x + 1 by the given three points.
Now for C( α , β ) ≡ ( α , α 2 + α + 1 )
Now writing area of Δ B C D in coordinates form
we obtain A = 2 − 3 x 2 + 3 x + 6 Differentiating and equating to zero
x = 2 1 = α
β = 7 / 4
Hence
a + b + c + 2 α + 4 β = 1 + 1 + 1 + 2 ( 2 1 ) + 4 ( 4 7 ) = 1 1
Good work +1 ! But there is even more shorter method ! Think , It is also interesting !
Log in to reply
I think i got the other way using slope at ( α , β ) and equating it to slope at BD to maximise it .Is it right?
Log in to reply
hmm ..yes , Gives It's explanation .
Log in to reply
@Deepanshu Gupta – Coz when they are parallel the distance bw them will be max and hence Δ = 2 b a s e × h e i g h t will be max.
Why did u equate the slopes??
Main i just failed but I go to 1 graid
Actually I think the 'Level 5' label and the 39% correct rate doesn't match the real difficulty of this question...
First, it has friendly give out three points on the parabola, so we have: ⎩ ⎪ ⎨ ⎪ ⎧ 4 a − 2 b + c = 3 a − b + c = 1 4 a + 2 b + c = 7
Easy to know that a = b = c = 1 , so the equation of the parabola is y = x 2 + x + 1 .
For A , B , D are fixed points, S △ A B D is a fixed value. So we can just consider when S △ B D C has maximum value.
Think the edge B D as the base of △ B D C , which is fixed, and when does the height has maximun value? The answer is when B D ∥ Tangent of the parabola through point C .
So we have, S l o p e B D = d x d y ∣ ∣ ∣ x = α , which is 2 = 2 α + 1 .
It is obivious that α = 1 / 2 , and β = 7 / 4 . Substitute a , b , c , α , β into the origin fomula and we'll have 1 1 .
The equation, as can be easily found by using the given points is x 2 + x + 1
Now, observe that area of triangle A B D is fixed, hence all we have to do is maximize area of triangle B C D . Since base B D is fixed, all that's left to do is to maximize perpendicular distance of C from B D . This happens when the tangent at point C has same value as the slope of line connecting B and D . Since in a parabola, the slope at a given point is proportional to its x coordinate, the coordinate α that we are looking for will be the A.M of B and D . ⇒ α = 1 / 2
Hence answer is 1 1
On an interesting note, we could have found out α without finding the equation of the curve! We had to find it only because of a , b , c !