Edge Case Of Rolling!
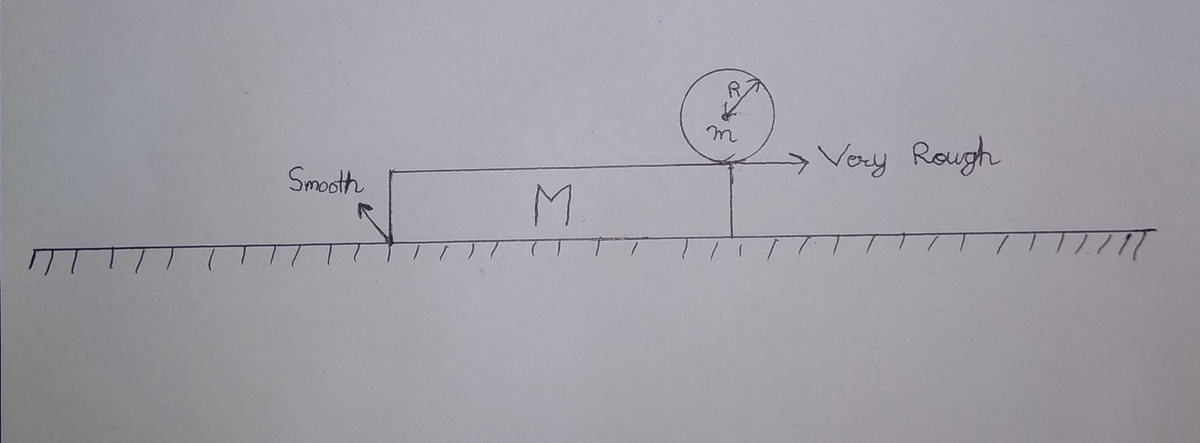
On the edge of a cuboidal plank of mass M = 8 kg , a uniform solid spherical ball of mass m = 1 2 kg and radius R is kept. The ball is given a very slight push towards right. There is no friction between plank and ground and friction between ball and plank is sufficient to prevent slipping . The plank won't topple during the journey.
If when ball just loses contact with plank, the angle made by Center of Mass ball with vertical is θ , then cos θ = 3 a − b where a , b ∈ I + Enter your answer as a + b .
Inspiration Aniket Sanghi
All of my problems are original .
The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
when the ball is in contact with the wedge, the point of the ball that is in contact has the same acceleration as the wedge, up until just before losing contact. the angular velocity must obey this constraint up until just before losing contact. the angular velocity cannot change instantaneously, it is the same right before and right after losing contact. thus, we should use this constraint in determining the angular velocity right after losing contact. your approach in determining this angular velocity requires that the point that was in contact, has no acceleration along the radius, which we do not know for sure once contact has been lost. i got your answer, but i think the correct answer is (7 - 2 sqrt 7) / 3.
Log in to reply
Sir, you said in your statement that angular velocity cannot change instantaneously, . So, I found the angular velocity just before losing contact, which is equal to angular velocity just after losing contact. Also, I asked the angle made by ball with vertical just after it loses contact, which is equal to angle with vertical just before it loses contact, which I found in solution. Also sir, I conserved energy of ball in ball's COM frame, so whether or not the contact point has acceleration doesn't matter. Hope it helps sir. :)
Log in to reply
mu^2 / R = mg cos theta, requires that the point of contact has no acceleration along the radius, we do not know for sure if this is true. what we do know is that the angular velocity upon losing contact must obey the constraint that the acceleration of the wedge and of the contact point must be the same before losing contact, which you totally ignored in your solution. also you cannot apply conservation of energy in an accelerating frame. would you like me to post my solution?
Log in to reply
@Ramon Vicente Marquez – Actually sir, I did include the constraint. In solution, you can see that As there is no slipping(i.e. acceleration of contact point of both wedge and ball is same) so ω = r u . Also sir, for any rotating/rolling body, acceleration of any point w.r.t. COM is mu^2/d where d is distance from COM(true for any point other than COM also). You could write the FBD and I think you too would get mu^2/r = mg cos theta. Hope it helps sir. :)
Log in to reply
@Aryan Sanghi – incorrect. for the general plane motion of a rigid body (translation and rotation in 2 dimensions), the relative acceleration between two points of the rigid body has a radial component (omega^2 R) and a tangential component (alpha R). in engineering mechanics, this is known as the pole method of acceleration analysis. this method is derived from the concept of related rates in calculus. please see my solution to see how this is applied.
acceleration, unlike velocity, can change instantaneously upon losing contact. the radial component of the COM acceleration just after losing contact, g cos theta, is not necessarily the same as the centripetal acceleration just before losing contact, u^2 / R. although the normal force approaches zero just before losing contact, friction does not necessarily approach zero. this is because there must be enough friction to prevent slipping while there is contact.
looking at your solution, we have the same equation for energy conservation, we both did it in the rest frame.
@Aryan Sanghi , this is my solution, try working out how i got cos theta = (7 - 2 sqrt 7) / 3.
@Aryan Sanghi , you might want to review your solution. there could be something wrong with it, that's why there's only two of us who got this problem, and the only solver aside from you, which is me, thinks that your solution is wrong.
Log in to reply
I'll see to it sir. Thanks for your review of the question. :)
Log in to reply
let me know what you think of my solution

When ball leaves the plank, let the velocity of plank be v and velocity of ball w.r.t. plank be u and angular velocity of ball be ω
Relating u , v and ω
Applying conservation of momentum in horizontal direction
m ( u cos θ − v ) = M v v = M + m m u cos θ
Also, as there is no slipping, therfore
ω = R u
Finding cos θ
Applying conservation of energy
m g R ( 1 − cos θ ) = 2 1 M v 2 + 2 1 m ( u cos θ − v ) 2 + 2 1 m ( u sin θ ) 2 + 2 1 I ω 2
2 m g R ( 1 − cos θ ) = M ( M + m m u cos θ ) 2 + m ( M + m M u cos θ ) 2 + m ( u sin θ ) 2 + 5 2 m u 2
u 2 = 7 M 2 + m 2 ( 7 − 5 cos 2 θ ) + M m ( 1 4 − 5 cos 2 θ ) 1 0 g R ( M + m ) 2
Now, when ball loses contact with wedge, N = 0 and so R m u 2 = m g cos θ or u 2 = g R cos θ .
g R cos θ = 7 M 2 + m 2 ( 7 − 5 cos 2 θ ) + M m ( 1 4 − 5 cos 2 θ ) 1 0 g R ( M + m ) 2
5 m cos 3 θ − 1 7 ( M + m ) cos θ + 1 0 ( M + m ) = 0
6 0 cos 3 θ − 3 4 0 cos θ + 2 0 0 = 0
cos θ = 3 2 4 − 3
Visualisation: Ball leaves wedge at angle 5 0 . 7 2 8 7 ° with vertical.