Electric Disc!

Electricity and Magnetism Level 5

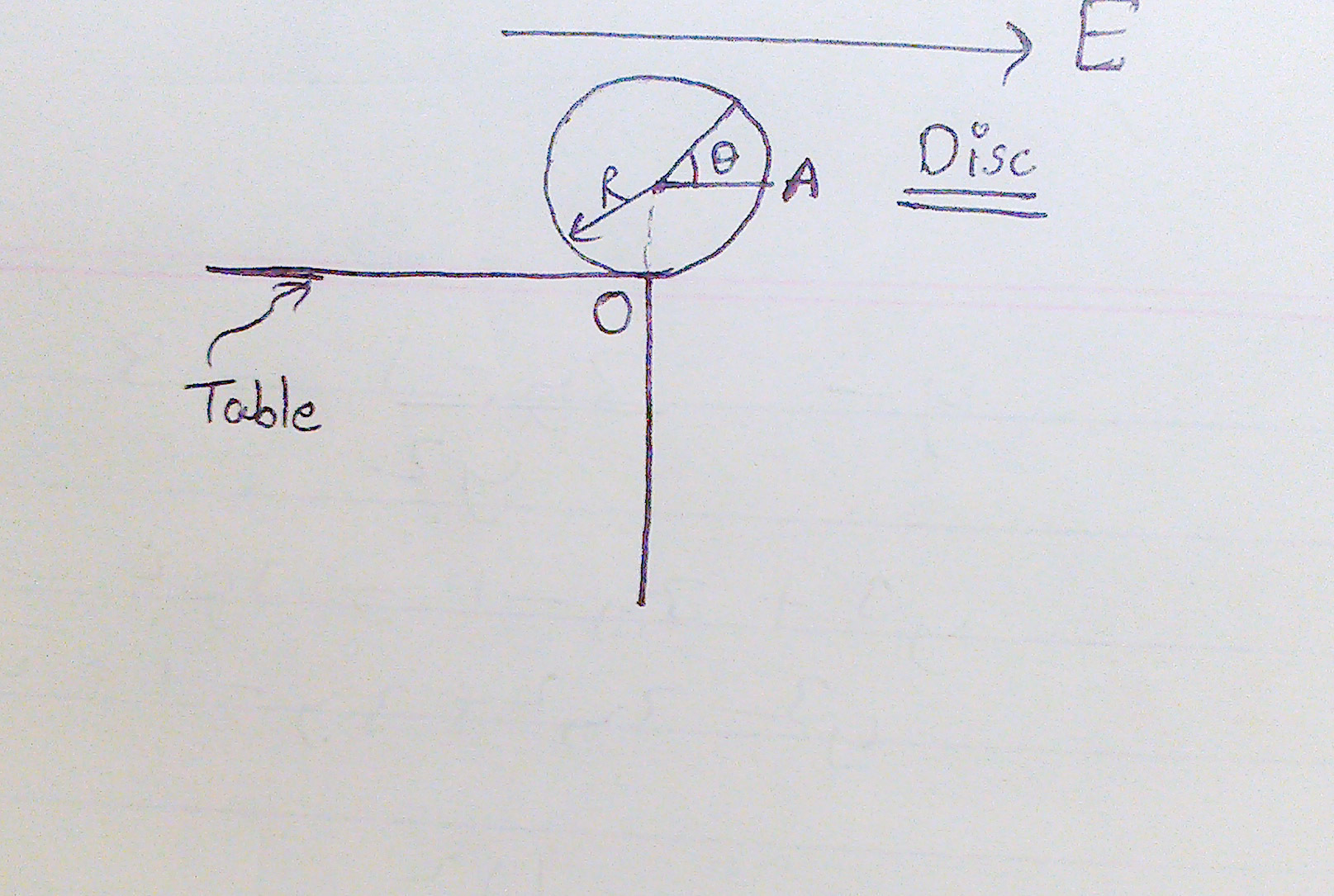
A disc of mass $m = 2\text{ kg}$ and Radius $R = 2\text{ m}$ is kept at the edge of the table. A non-uniform charge is distributed on the circumference of the disc whose linear charge density varies as $\large{\lambda = \dfrac{\sin\theta}{\pi}}$ ( $\theta$ is measured from point $A$ ). A uniform horizontal electric field exist in the region as shown.

What is the angle the disc makes with the vertical when it loses contact with the table.

Your answer can be represented as ${ \phi = {\cos}^{-1}(\dfrac{a}{b\sqrt {c}}) - \dfrac{\pi}{4}}$ .

Enter your answer as $a \times b \times c$ .

Details and Assumptions :

Electric field $E = 17.5 N/C$ , take $g = 10 m/s^2$
Angle ( $\phi$ ) is measured clockwise.
Disc is not a conductor.
a , b and c are positive integers and c is a square free integer.
Friction is sufficient.

Wanna! Try q on mixing of concepts click here

The answer is 56.

3 solutions

Aryan Goyat
May 17, 2016

so at any general angle alpha with the vertical E can be replaced by Ecos(alpha)

so net torque at an angle alpha =ER^(2)cos(alpha)+mgRsin(alpha)

but this equals 3/2mR^{2}(Angular Acc)

Angular Acc=/ $\frac{wd(w)}{d(alpha)}$

mw^(2)r=140(sin(alpha))/3+80/3(1-cos(alpha))

{as net force due to E=O as net charge on disc=0 }

hence we write mw^{2}R=mgcos(alpha)

cos(alpha +pi/4)=4/7root(2)

Right! I did it by using concept of electric dipole :)

Aniket Sanghi - 5 years ago

ok would love to see your approach too

aryan goyat - 5 years ago

about which point you have considered torque?? i cant see where the mg term came from..if i take torque about centre!!

Abhash Jha - 4 years, 1 month ago

Arunava Das
Jan 23, 2018

You can find out the net work done by the field, on rotation of the disc about the point of contact, and the work done by gravity. The sum of these will equate the instantaneous KE of the disc. Then from KE find omega at that instant. Now the normal force equals zero, i.e. component of mg along line joining COM and point of contact equals mw^r when the disc is losing contact. A simple diagram will ease things, and there is frankly little calculation. (P.S. I don't know how to use latex, so cannot post a solution or diagram)

It would just work if we take the $qE \times R \sin \phi$ for work done by Electric field na?

Md Zuhair - 3 years, 2 months ago

A Former Brilliant Member
Dec 15, 2016

i did it using the concept of centre of charge , and treating the half discs as point charges (it works just like the com concept ! :))

can u provide a solution .im not quiet able to follow u

avi solanki - 4 years, 4 months ago

see it as a disc which has mass distribution as given in problem and then find it's COM, then apply the force oon it's com to find the torkue :)

A Former Brilliant Member - 4 years, 4 months ago

thank u shubham