Electric Field due to $K$

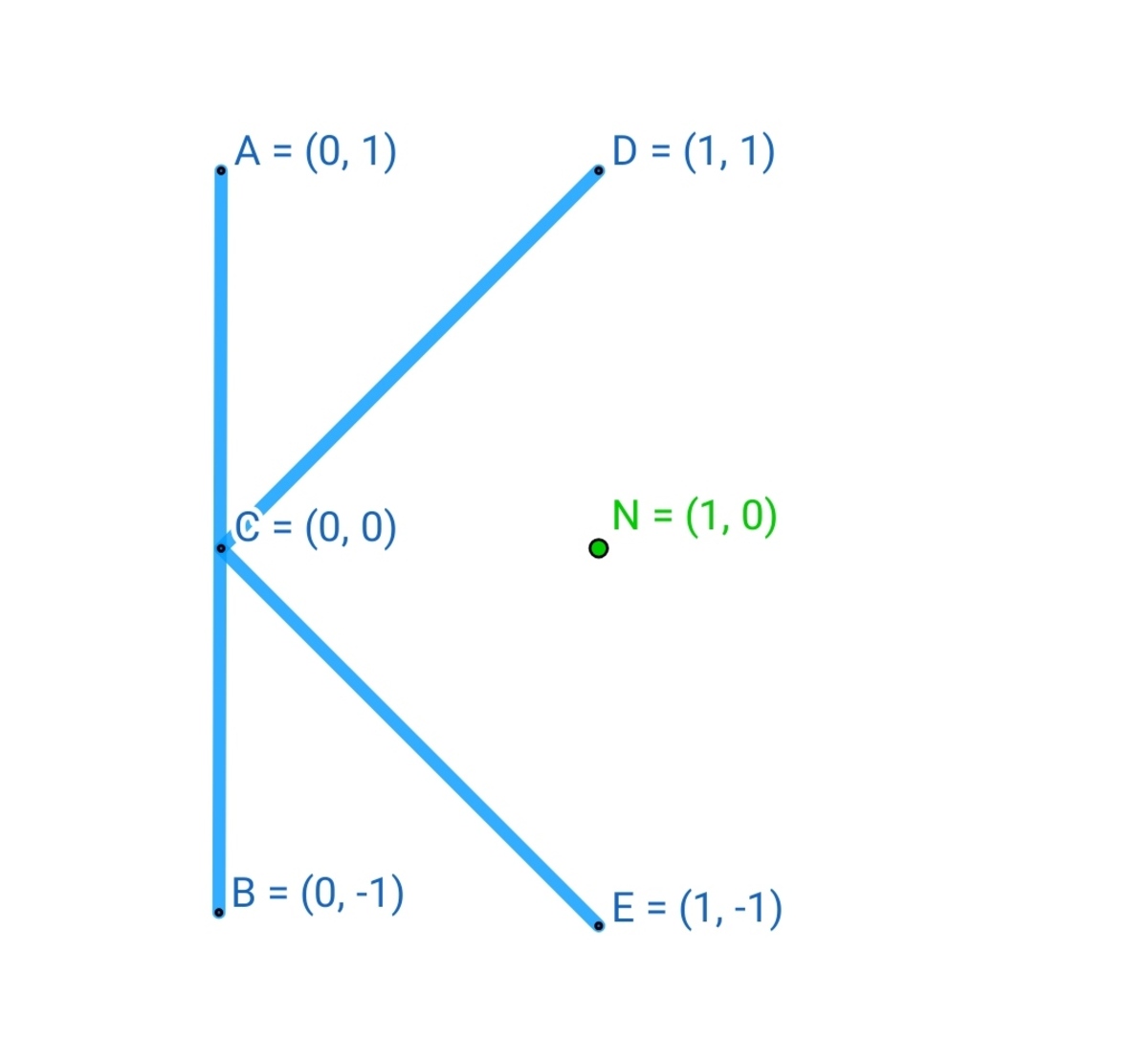
Electricity and Magnetism Level pending

Three rods $AB, CD, CE$ are placed in the $xy$ plane has a uniform linear charge density $\lambda=1$ . Find the magnitude of (Electric field) $E$ at the point $N(1, 0)$ This question is dedicated to my teacher Karan Chatrath. Take $\epsilon_{0}=1$ . All the things are in SI units

The answer is 0.337.

2 solutions

Steven Chase
Apr 18, 2020

Thanks to the problem author for re-posting this problem. I deleted my first solution to make adjustments to some of the nomenclature, but I then found that I didn't have an opportunity to upload a solution again. That's good to know going forward.

I renamed points $D$ and $E$ to $F$ and $G$ respectively, because I have other uses for $D$ and $E$ in my code. I used a repeated segment of script code as a poor man's function call. This way, one can simulate arbitrarily many line segments just by copying the script code segment, and changing the starting and ending coordinates $(x_1, y_1, z_1)$ and $(x_2, y_2, z_2)$ .

import math

#######################################

# General params

Num = 10**5

e0 = 1.0
k = 1.0/(4.0*math.pi*e0)

lam = 1.0 # charge density

#######################################

# Coordinates

Ax = 0.0
Ay = 1.0
Az = 0.0

Bx = 0.0
By = -1.0
Bz = 0.0

Cx = 0.0
Cy = 0.0
Cz = 0.0

Fx = 1.0
Fy = 1.0
Fz = 0.0

Gx = 1.0
Gy = -1.0
Gz = 0.0

Nx = 1.0
Ny = 0.0
Nz = 0.0

#######################################

# Initialize field 

Ex = 0.0
Ey = 0.0
Ez = 0.0

#######################################

# A to B

x1 = Ax
y1 = Ay
z1 = Az

x2 = Bx
y2 = By
z2 = Bz

Lx = x2 - x1
Ly = y2 - y1
Lz = z2 - z1

L = math.sqrt(Lx**2.0 + Ly**2.0 + Lz**2.0)

dq = lam*L/Num

dx = Lx/Num
dy = Ly/Num
dz = Lz/Num

x = x1
y = y1
z = z1

for j in range(0,Num):

    Dx = Nx - x
    Dy = Ny - y
    Dz = Nz - z

    D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

    ux = Dx/D
    uy = Dy/D
    uz = Dz/D

    dE = k*dq/(D**2.0)

    dEx = dE * ux
    dEy = dE * uy
    dEz = dE * uz

    Ex = Ex + dEx
    Ey = Ey + dEy
    Ez = Ez + dEz

    x = x + dx
    y = y + dy
    z = z + dz

#######################################

# C to F

x1 = Cx
y1 = Cy
z1 = Cz

x2 = Fx
y2 = Fy
z2 = Fz

Lx = x2 - x1
Ly = y2 - y1
Lz = z2 - z1

L = math.sqrt(Lx**2.0 + Ly**2.0 + Lz**2.0)

dq = lam*L/Num

dx = Lx/Num
dy = Ly/Num
dz = Lz/Num

x = x1
y = y1
z = z1

for j in range(0,Num):

    Dx = Nx - x
    Dy = Ny - y
    Dz = Nz - z

    D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

    ux = Dx/D
    uy = Dy/D
    uz = Dz/D

    dE = k*dq/(D**2.0)

    dEx = dE * ux
    dEy = dE * uy
    dEz = dE * uz

    Ex = Ex + dEx
    Ey = Ey + dEy
    Ez = Ez + dEz

    x = x + dx
    y = y + dy
    z = z + dz

#######################################

# C to G

x1 = Cx
y1 = Cy
z1 = Cz

x2 = Gx
y2 = Gy
z2 = Gz

Lx = x2 - x1
Ly = y2 - y1
Lz = z2 - z1

L = math.sqrt(Lx**2.0 + Ly**2.0 + Lz**2.0)

dq = lam*L/Num

dx = Lx/Num
dy = Ly/Num
dz = Lz/Num

x = x1
y = y1
z = z1

for j in range(0,Num):

    Dx = Nx - x
    Dy = Ny - y
    Dz = Nz - z

    D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

    ux = Dx/D
    uy = Dy/D
    uz = Dz/D

    dE = k*dq/(D**2.0)

    dEx = dE * ux
    dEy = dE * uy
    dEz = dE * uz

    Ex = Ex + dEx
    Ey = Ey + dEy
    Ez = Ez + dEz

    x = x + dx
    y = y + dy
    z = z + dz

#######################################

# Results

print Num
print ""
print Ex
print Ey
print Ez
print ""

E = math.sqrt(Ex**2.0 + Ey**2.0 + Ez**2.0)

print E

#######################################

#>>> 
#100000

#0.337619743946
#-5.62697657954e-07
#0.0

#0.337619743946
#>>> ================================ RESTART ================================
#>>> 
#1000000

#0.337618731099
#-5.62704983227e-08
#0.0

#0.337618731099
#>>>

@Steven Chase welcome. What is the meaning of poor man's function call?

A Former Brilliant Member - 1 year, 1 month ago

It would be possible to package up that repeated code module and make it a function. And then, having defined the function, I could just pass in arguments to the function and make a function call, and the function would return the electric field contributions. Copying a script segment over and over is an alternative to repeatedly calling a function.

Steven Chase - 1 year, 1 month ago

@Steven Chase I have corrected that question Electric flux exercise

A Former Brilliant Member - 1 year, 1 month ago

@A Former Brilliant Member – How is an electric flux generated, since the charges are in the same plane as the loop?

Steven Chase - 1 year, 1 month ago

@Steven Chase – @Steven Chase Sir charge are not on the same plane, due to projectile motion they are in $x-z$ plane And gravity is acting in $-z$ direction.

A Former Brilliant Member - 1 year, 1 month ago

@A Former Brilliant Member – Oh, I missed the part where it says to find the answer at $t = 1$ . I don't think that was there originally

Steven Chase - 1 year, 1 month ago

@A Former Brilliant Member – I don't have any remaining tries since I viewed the answer

Steven Chase - 1 year, 1 month ago

@Steven Chase – @Steven Chase yes sir it wasn't originally there. I accept my mistake. I have reposted the question

A Former Brilliant Member - 1 year, 1 month ago

@A Former Brilliant Member – Ok, thanks. I'll try it

Steven Chase - 1 year, 1 month ago

Karan Chatrath
Apr 19, 2020

Thanks for posting this problem. I did this analytically as follows. Consider a charged wire where a point has the following position vector:

$\vec{r}_p = x \hat{i} + y \hat{j} + 0 \hat{k}$

The point (on the X-Y plane) at which the electric field is to be computed is:

$\vec{r}_c = x_o \hat{i} + y_o \hat{j} + 0 \hat{k}$

The charge on an elementary arc length near a point on the wire is:

$dQ = \lambda \sqrt{(dx)^2 + (dy)^2}$

The elementary electric field is:

$d\vec{E} = \frac{dQ}{4 \pi}\left(\frac{ \vec{r}_c-\vec{r}_p}{\lvert \vec{r}_c-\vec{r}_p \rvert^3}\right)$

Each of the components can be integrated (between specified limits) to obtain the resultant field in the X and Y directions.

Using this recipe to compute the electric field due to the vertical wire leads to the result:

$\vec{E}_1 = \frac{\sqrt{2}}{4 \pi}\left(\hat{i} + 0 \hat{j}\right)$

For the wire along the line $y=x$ , the electric field is:

$\vec{E}_2 = \frac{\sqrt{2}}{4 \pi}\left( \hat{i} -\hat{j}\right)$

For the wire along the line $y=-x$ , the electric field is:

$\vec{E}_3 = \frac{\sqrt{2}}{4 \pi}\left( \hat{i} +\hat{j}\right)$

The net electric field is:

$\boxed{\vec{E} = \vec{E}_2+\vec{E}_2+\vec{E}_3= \frac{3\sqrt{2}}{4 \pi} \hat{i}}$

@Karan Chatrath sir for solid non-conducting sphere $E(r)=Er^{2}$ $\rho (r) =?$ Thanks in advance

A Former Brilliant Member - 1 year ago

Is the direction of the field radial?

Karan Chatrath - 1 year ago

@Karan Chatrath sir can you please help me in this question, lim $\frac{x^{6000}-(sinx)^{6000}}{x^{2}(sinx) ^{6000}}$
x tends to 0
I hope I am not disturbing you.
Thanks in advance.
If there are two method I will be very happy.

A Former Brilliant Member - 1 year ago

@Karan Chatrath Yes it's radial

A Former Brilliant Member - 1 year ago

You need to make use of one of Maxwell's equations (Basically Gauss's law modified)

Consider:

$\vec{E} = E r^2 \hat{r}$

$\vec{E} = E\left(x\sqrt{x^2+y^2+z^2} \ \hat{i} + y\sqrt{x^2+y^2+z^2} \ \hat{j} + z\sqrt{x^2+y^2+z^2} \ \hat{k} \right)$

$\nabla \cdot \vec{E} = 4E\sqrt{x^2+y^2+z^2} = 4Er$

Here $E$ is assumed constant. From Maxwell's version of Gauss' law:

$\nabla \cdot \vec{E} = \frac{\rho}{\epsilon_o}$

$\implies \boxed{\rho = 4E \epsilon_o r}$

Karan Chatrath - 1 year ago

@Karan Chatrath Thankyou very much

A Former Brilliant Member - 1 year ago

@Karan Chatrath Sir If one of the plates of a capacitor is halved , will there be any change in the capacitance of the capacitor and how much?
Please explain

A Former Brilliant Member - 1 year ago

Consider the simple case where the space between the plates is small and the plates are much larger in dimensions in comparison with the space $d$ . In this case, the formula for electric field:

$E = \frac{\sigma}{2 \epsilon_o}$

still applies. So the charge on each plate will be equal due to the law of conservation of charge. Calculate the electric field due to each of the plates. Then compute the net electric field due to each of the plates. Using that constant field, the potential difference can be computed, and finally the capacitance. So yes, the charge on each plate will be the same but the capacitance will be different.

Try this calculation by yourself. Hope I made sense.

Karan Chatrath - 1 year ago

@Karan Chatrath yes I have used this formula. I am getting answer as $\frac{2}{3}C$ if the original capacitance was $C$ but the answer given in my book is $0.5C$ ?

A Former Brilliant Member - 1 year ago

@A Former Brilliant Member – I get $4C/3$ . This approach that I described seems logical to me. And books are not always correct.

Karan Chatrath - 1 year ago

Electric Field due to K K K

The answer is 0.337.

2 solutions

0 pending reports

Electric Field due to $K$