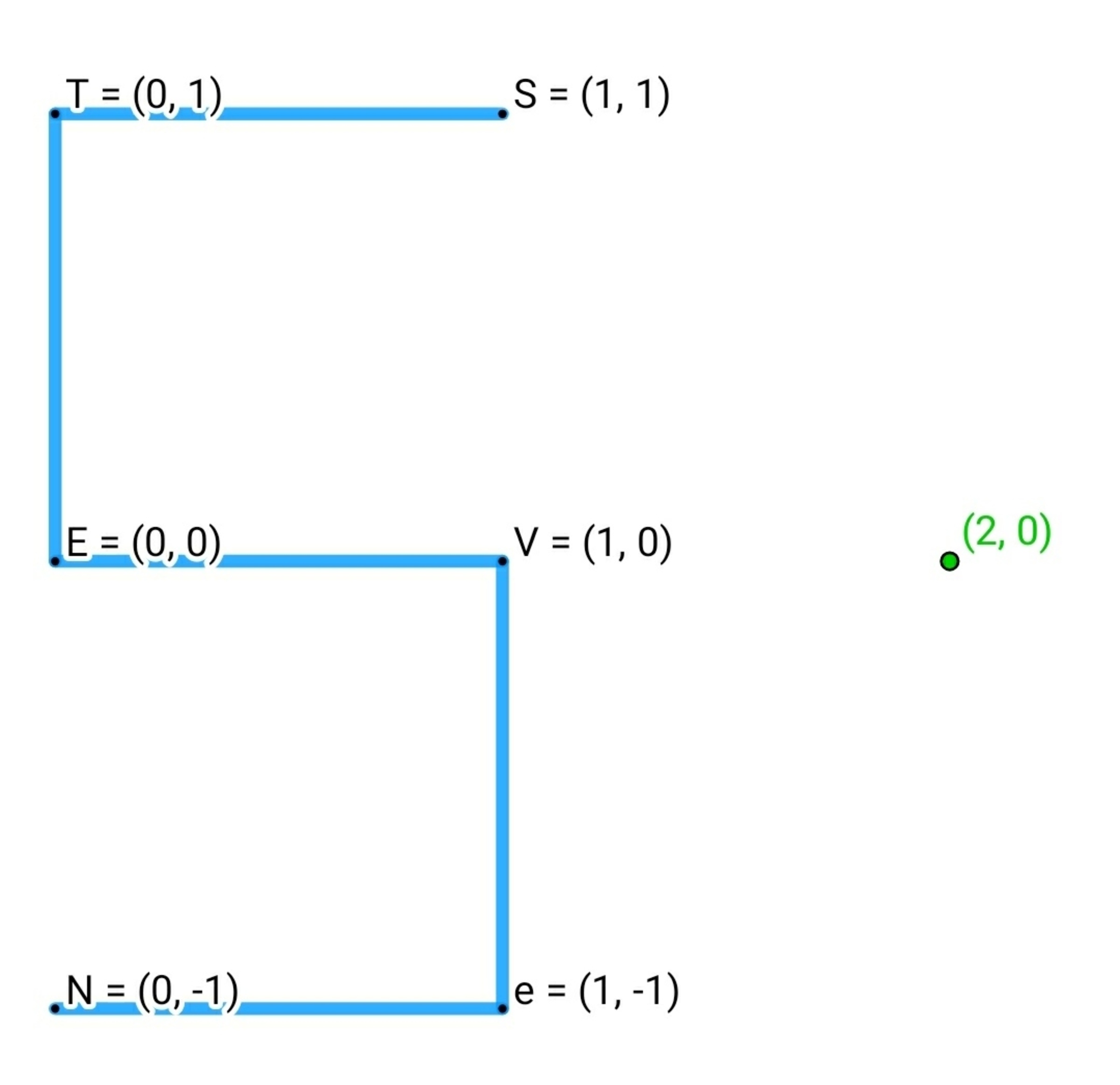
Electric Field due to $\textcolor{#3D99F6}{S}$

Electricity and Magnetism Level pending

Five rods $ST,TE,EV,Ve,eN$ are placed in the $xy$ plane has a uniform linear charge density $\lambda=1$ . Find the magnitude of (Electric field) $E$ at the point $(2,0)$ This question is dedicated to my teacher Steven Chase. Take $\epsilon_{0}=1$ . All the things are in SI units

The answer is 0.156.

2 solutions

Steven Chase
Apr 20, 2020

Thanks for dedicating the problem. I slightly modified the code from the "K" problem.

import math

#######################################

# General params

Num = 10**5

e0 = 1.0
k = 1.0/(4.0*math.pi*e0)

lam = 1.0 # charge density

#######################################

# Coordinates

x1 = 1.0
y1 = 1.0
z1 = 0.0

x2 = 0.0
y2 = 1.0
z2 = 0.0

x3 = 0.0
y3 = 0.0
z3 = 0.0

x4 = 1.0
y4 = 0.0
z4 = 0.0

x5 = 1.0
y5 = -1.0
z5 = 0.0

x6 = 0.0
y6 = -1.0
z6 = 0.0

x7 = 2.0
y7 = 0.0
z7 = 0.0

#######################################

# Initialize field 

Ex = 0.0
Ey = 0.0
Ez = 0.0

#######################################

# 1 to 2

P1x = x1
P1y = y1
P1z = z1

P2x = x2
P2y = y2
P2z = z2

Lx = P2x - P1x
Ly = P2y - P1y
Lz = P2z - P1z

L = math.sqrt(Lx**2.0 + Ly**2.0 + Lz**2.0)

dq = lam*L/Num

dx = Lx/Num
dy = Ly/Num
dz = Lz/Num

x = P1x
y = P1y
z = P1z

for j in range(0,Num):

    Dx = x7 - x
    Dy = y7 - y
    Dz = z7 - z

    D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

    ux = Dx/D
    uy = Dy/D
    uz = Dz/D

    dE = k*dq/(D**2.0)

    dEx = dE * ux
    dEy = dE * uy
    dEz = dE * uz

    Ex = Ex + dEx
    Ey = Ey + dEy
    Ez = Ez + dEz

    x = x + dx
    y = y + dy
    z = z + dz

#######################################

# 2 to 3

P1x = x2
P1y = y2
P1z = z2

P2x = x3
P2y = y3
P2z = z3

Lx = P2x - P1x
Ly = P2y - P1y
Lz = P2z - P1z

L = math.sqrt(Lx**2.0 + Ly**2.0 + Lz**2.0)

dq = lam*L/Num

dx = Lx/Num
dy = Ly/Num
dz = Lz/Num

x = P1x
y = P1y
z = P1z

for j in range(0,Num):

    Dx = x7 - x
    Dy = y7 - y
    Dz = z7 - z

    D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

    ux = Dx/D
    uy = Dy/D
    uz = Dz/D

    dE = k*dq/(D**2.0)

    dEx = dE * ux
    dEy = dE * uy
    dEz = dE * uz

    Ex = Ex + dEx
    Ey = Ey + dEy
    Ez = Ez + dEz

    x = x + dx
    y = y + dy
    z = z + dz

#######################################

# 3 to 4

P1x = x3
P1y = y3
P1z = z3

P2x = x4
P2y = y4
P2z = z4

Lx = P2x - P1x
Ly = P2y - P1y
Lz = P2z - P1z

L = math.sqrt(Lx**2.0 + Ly**2.0 + Lz**2.0)

dq = lam*L/Num

dx = Lx/Num
dy = Ly/Num
dz = Lz/Num

x = P1x
y = P1y
z = P1z

for j in range(0,Num):

    Dx = x7 - x
    Dy = y7 - y
    Dz = z7 - z

    D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

    ux = Dx/D
    uy = Dy/D
    uz = Dz/D

    dE = k*dq/(D**2.0)

    dEx = dE * ux
    dEy = dE * uy
    dEz = dE * uz

    Ex = Ex + dEx
    Ey = Ey + dEy
    Ez = Ez + dEz

    x = x + dx
    y = y + dy
    z = z + dz

#######################################

# 4 to 5

P1x = x4
P1y = y4
P1z = z4

P2x = x5
P2y = y5
P2z = z5

Lx = P2x - P1x
Ly = P2y - P1y
Lz = P2z - P1z

L = math.sqrt(Lx**2.0 + Ly**2.0 + Lz**2.0)

dq = lam*L/Num

dx = Lx/Num
dy = Ly/Num
dz = Lz/Num

x = P1x
y = P1y
z = P1z

for j in range(0,Num):

    Dx = x7 - x
    Dy = y7 - y
    Dz = z7 - z

    D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

    ux = Dx/D
    uy = Dy/D
    uz = Dz/D

    dE = k*dq/(D**2.0)

    dEx = dE * ux
    dEy = dE * uy
    dEz = dE * uz

    Ex = Ex + dEx
    Ey = Ey + dEy
    Ez = Ez + dEz

    x = x + dx
    y = y + dy
    z = z + dz

#######################################

# 5 to 6

P1x = x5
P1y = y5
P1z = z5

P2x = x6
P2y = y6
P2z = z6

Lx = P2x - P1x
Ly = P2y - P1y
Lz = P2z - P1z

L = math.sqrt(Lx**2.0 + Ly**2.0 + Lz**2.0)

dq = lam*L/Num

dx = Lx/Num
dy = Ly/Num
dz = Lz/Num

x = P1x
y = P1y
z = P1z

for j in range(0,Num):

    Dx = x7 - x
    Dy = y7 - y
    Dz = z7 - z

    D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

    ux = Dx/D
    uy = Dy/D
    uz = Dz/D

    dE = k*dq/(D**2.0)

    dEx = dE * ux
    dEy = dE * uy
    dEz = dE * uz

    Ex = Ex + dEx
    Ey = Ey + dEy
    Ez = Ez + dEz

    x = x + dx
    y = y + dy
    z = z + dz

#######################################

# Results

print Num
print ""
print Ex
print Ey
print Ez
print ""

E = math.sqrt(Ex**2.0 + Ey**2.0 + Ez**2.0)

print E

#######################################

#>>> 
#10000

#0.155216549358
#0.0191053304864
#0.0

#0.156387949816
#>>> ================================ RESTART ================================
#>>> 
#100000

#0.155215923795
#0.0191069169207
#0.0

#0.156387522756
#>>>

@Steven Chase sir can you please help me in this question, lim $\frac{x^{6000}-(sinx)^{6000}}{x^{2}(sinx) ^{6000}}$
x tends to 0

Thanks in advance.
If there are two method I will be very happy.

A Former Brilliant Member - 1 year ago

Is the answer 1000? If so, I'll tell you how I got it

Steven Chase - 1 year ago

@Steven Chase correct answer is 2

A Former Brilliant Member - 1 year ago

@Steven Chase can we solve this types of questions through code also.??

A Former Brilliant Member - 1 year ago

@A Former Brilliant Member – The exponents are way too big for a code solution to be reliable

Steven Chase - 1 year ago

@Steven Chase – @Steven Chase My Mathematics sir has challenged whole class (especially me) to solve this limit problem till today night. Please. Can you do something.

A Former Brilliant Member - 1 year ago

@Steven Chase – @Steven Chase I was solving in this way $\Large \frac{x^{6000}-(sinx)^{6000}}{x^{6002}\frac{(sinx)^{6000}}{x^{6000}}}$

A Former Brilliant Member - 1 year ago

@A Former Brilliant Member – He told you in advance that the answer is 2, and he just wants you to prove it?

Steven Chase - 1 year ago

@Steven Chase – @Steven Chase He is not so serious man, sometimes he says that wrong as the correct answer to divert the students. I think at the end of class he said that 2 is the correct answer. I don't know it is correct or not, but I think he was serious at that time.

A Former Brilliant Member - 1 year ago

@A Former Brilliant Member – @Steven Chase sir did you understand what I wanted to say??

A Former Brilliant Member - 1 year ago

@A Former Brilliant Member – Ok, here's what I've got. Let's see if you can find something wrong. First, take the first two terms of the Taylor expansion for $\sin(x)$ .

$\sin(x) \approx x - \frac{x^3}{6}$

For small $x$ , the higher-order terms should be negligible. Now use Pascal's Triangle to get the first two terms of $(\sin x)^{6000}$ .

$(\sin x )^{6000} = (x - \frac{x^3}{6})^{6000} \approx x^{6000} + 6000 x^{5999} \Big(- \frac{x^3}{6} \Big) = x^{6000} - 1000 x^{6002}$

Plugging into the original expression and taking the limit as $x$ goes to zero:

$\frac{x^{6000} - x^{6000} + 1000 x^{6002} }{x^{6002} - 1000 x^{6004}}$

This results in $1000$

Steven Chase - 1 year ago

@Steven Chase – Ohhhh sorry

A Former Brilliant Member - 1 year ago

@Steven Chase – @Steven Chase Please forgive me, The main problem was that after the result divide the answer by 500.Sorry!

A Former Brilliant Member - 1 year ago

@A Former Brilliant Member – Excellent. So I guess we're good then

Steven Chase - 1 year ago

@Steven Chase – @Steven Chase Yes. Thanks.
Can we have 1 more method

A Former Brilliant Member - 1 year ago

@A Former Brilliant Member – Maybe you could try L'Hospital as well. But that seems tedious

Steven Chase - 1 year ago

@Steven Chase – @Steven Chase could you please solve??I am also solving. How much time we have to apply it, 6000,hahA

A Former Brilliant Member - 1 year ago

@A Former Brilliant Member – I wondered the same thing. That's why I went with the expansion route instead.

Steven Chase - 1 year ago

@Steven Chase – @Steven Chase Beside this both, can we have another 3rd route, it would be very great. But if we apply LHospital It will come as, if we differentiate 6000 time, $6000!-6000sin^{5999}cosx$ In the Numerator Edited (negative sign)

A Former Brilliant Member - 1 year ago

@A Former Brilliant Member – @Steven Chase my upper comment is wrong. We will not give up now, I think we can do this through .LHospital

A Former Brilliant Member - 1 year ago

@Steven Chase – @Steven Chase are you trying it with LHospital , or any other way?

A Former Brilliant Member - 1 year ago

@A Former Brilliant Member – Given that I've found one solution already, I'm going to leave it where it is. Good luck

Steven Chase - 1 year ago

@Steven Chase – @Steven Chase OH YEAH! I think you don't want to waste your time?? Correct! Your are very smart person. BTW when I am applying LHospital I am following a particular series trend, hope it will reach to my correct answer.

A Former Brilliant Member - 1 year ago

@Steven Chase sir I have installed the latest version of python in my computer. But I am not getting that page where I will run the code??
Suggest me something from where should I learn???

A Former Brilliant Member - 11 months, 3 weeks ago

You have to open the GUI, which is called IDLE

Steven Chase - 11 months, 3 weeks ago

Sir from this where should I go
And where is GUI located. Please can you help me little bit in starting of this things.

A Former Brilliant Member - 11 months, 3 weeks ago

@A Former Brilliant Member – Try typing IDLE in the search bar

Steven Chase - 11 months, 3 weeks ago

@Steven Chase – @Steven Chase I searched but nothing comes.

A Former Brilliant Member - 11 months, 3 weeks ago

@A Former Brilliant Member – When you were installing, there might have been a check box to say you wanted to install IDLE. Did you check it? If not, you may need to go back and install it separately.

Steven Chase - 11 months, 3 weeks ago

@Steven Chase – @Steven Chase ok sir let me on my computer and check now.
Please be connected for sometime, I will be grateful.

A Former Brilliant Member - 11 months, 3 weeks ago

@Steven Chase – @Steven Chase I downloaded it from here
After this where I have to go ??
Am i going right??

A Former Brilliant Member - 11 months, 3 weeks ago

@A Former Brilliant Member – I think IDLEX is an expansion for IDLE, which you don't have yet. Maybe the easier thing would be to un-install python and re-install it. And when you re-install, make sure you check the box to install IDLE

Steven Chase - 11 months, 3 weeks ago

@Steven Chase – @Steven Chase sir I am not able to find the file with name IDlE

A Former Brilliant Member - 11 months, 3 weeks ago

@A Former Brilliant Member – When you install Python, the wizard shows you a bunch of checkboxes that let you select what components you want to install. IDLE should be one of those. It's not a file, it's a checkbox option when you install

Steven Chase - 11 months, 3 weeks ago

@Steven Chase can you help me in this problem?

A Former Brilliant Member - 11 months ago

This is a pretty easy problem. You should have no trouble with it.

Steven Chase - 11 months ago

@Steven Chase yes I know . At $t=0$ should I assume $R=0$ and after $1$ min $R=5$ ??

A Former Brilliant Member - 11 months ago

@A Former Brilliant Member – At $t = 60$ , $R = 5$

Steven Chase - 11 months ago

@Steven Chase – @Steven Chase so I have to integrate 4 time steps
Right??

A Former Brilliant Member - 11 months ago

@A Former Brilliant Member – You have to use seconds, so you are integrating from $t = 0$ to $t = 240$

Steven Chase - 11 months ago

@Steven Chase – @Steven Chase Now I am going correct
$\int_{0}^{240} \frac{120dt}{240+t}=q_{total}$
I was solving by sleeping in bed.
Now it's a lesson for me to solve question by sitting properly.
Are you agree?

A Former Brilliant Member - 11 months ago

A Former Brilliant Member
May 23, 2020

The top, middle and bottom horizontal parts of the figure will contribute to electric field in the horizontal direction only, of total magnitude

$\dfrac{1}{2π}(\frac{1}{4}+\frac{1}{\sqrt 2}-\frac{1}{\sqrt 5})\approx 0.081152$ .

The two vertical parts will contribute a total field in the horizontal direction of magnitude

$\dfrac{1}{4π}(\frac{1}{2\sqrt 5}+\frac{1}{\sqrt 2 })\approx 0.07406$ .

So, the total field component along horizontal direction is $\approx 0.15521585$ .

The total field component along the vertical direction is due to the two vertical parts, and is of magnitude

$\dfrac{1}{4π}(\frac{1}{2}-\frac{1}{\sqrt 2 }+\frac{1}{\sqrt 5})\approx 0.019107$ .

Hence the total electric field is of magnitude

$\sqrt {(0.15521585)^2+(0.019107)^2}\approx \boxed {0.15638}$ .

Electric Field due to S \textcolor{#3D99F6}{S} S

The answer is 0.156.

2 solutions

0 pending reports

Electric Field due to $\textcolor{#3D99F6}{S}$