Electric fields due to different kinds of plates

Electricity and Magnetism Level 4

We have a triangular uniformly charged plate of charge density $\sigma$ .

We take a point just above a vertex of the triangular plate at a distance $d$ perpendicular to the plane of the triangle. Let the vertical component of electric field at that point be $E(d)$ in $V/m$

Find $\displaystyle \lim_{d \rightarrow 0}{E(d)}$

Details and Assumptions :

1) $\sigma = 10^{-9} C , {\epsilon}_{0}=8.85 \times {10}^{-12} \text{ SI units}$

2) The triangle is equilateral. By vertical component of electric field I mean electric field perpendicular to the plane of charge.

3) The plate is non conducting.

The answer is 9.416.

1 solution

Ronak Agarwal
May 6, 2015

Place more 5 such equilateral charged plates so as to complete the hexagon with the vertex close to D being the centre of the hexagon.

Now the electric field due to uniformly charged plate is given by = $\frac{\sigma}{2{\epsilon}_{0}}$ .

Also each triangle contributes equally inthe electric field hence divide by 6 to get the answer.

I feel that the question has been incorrectly stated. Only the vertical component of the electric field is $\sigma/12\epsilon_{0}$ . The horizontal component blows up. Please correct me if I am wrong.

Karthik Kannan - 6 years, 1 month ago

Thanks I have corrected it now.

Ronak Agarwal - 6 years, 1 month ago

@Karthik Kannan , I heard that you are enrolled in Engineering Physics course in IIT Bombay, I want to ask that how's the course, I mean is it interesting, since I also want to take this course. Please reply.

On 25th of June we have to fill our choices.

Ronak Agarwal - 5 years, 11 months ago

Hi Ronak Agarwal ! First of all I must congratulate you for your brilliant performance in JEE-Advanced. All first year students have common courses and I shall study courses in my own department only from the next semester. But this branch is surely great for all those who are enthusiastic about physics. You will have various courses in physics along with various courses in other engineering disciplines such as Electrical Engineering. I would advise you look at this to get an idea about the various courses in each department. Also look at this to help you make a good decision. All the best $\ddot\smile$

Karthik Kannan - 5 years, 11 months ago

Hey Ronak, this is completely off topic but really important:

IISC Bangalore has invited applicants to Bangalore on the 21st of May for a $compulsory$ counselling session. I guess you must have received the mail regarding the same.

So that's like 3 days before Advanced! Will you be going?(And is IISC still your first choice?)

@Ronak Agarwal

Shashwat Shukla - 6 years, 1 month ago

Yes I also got it today itself, and I was shocked to see the date of counselling 21st-May just three days before advanced also the main problem is banglore is far away from jaipur, in that case I have to go and return by plane.

But looks like I have to go anyway, but I am unable to make a first choice till now,

Also are you coming @Shashwat Shukla

Or is your priority only JEE, also how's your AITS Full test -9

Ronak Agarwal - 6 years, 1 month ago

I will be going for sure as I am very much interested in enrolling at IISC. Also, thankfully Kochi is far closer to Bangalore than Jaipur.

AITS-9 was better than 8 but still could have done better. I'm getting 278. How was it for you?

@Ronak Agarwal

Shashwat Shukla - 6 years, 1 month ago

@Shashwat Shukla – Good for me getting 335/360. Thankfully I have got to know someone who is interested in enrolling in IISC.

Ronak Agarwal - 6 years, 1 month ago

@Ronak Agarwal – Wow! That is an amazing score! Hats-off :)

Hope to meet you on the 21st if things work out. Good luck for the next AITS.

Shashwat Shukla - 6 years, 1 month ago

@Shashwat Shukla – I am coming surely, can you speak hindi. Shashwat. Looking forward to see you at IISC also is the counseling of one day only. (Just 3 days before advanced whoa.)

Ronak Agarwal - 6 years, 1 month ago

@Ronak Agarwal – I asked a senior of mine about the duration and he said that it only takes a day, as the number of applicants isn't $very$ high.

And I am sure they did this on purpose: 3 days before advanced was the only time they got? I guess they only want applicants who are actually planning to join to come.

Also, I do speak Hindi :D. This might be fun.

Shashwat Shukla - 6 years, 1 month ago

@Shashwat Shukla – Can you please tell me what will exactly happen in the counseling. Shashwat.

Ronak Agarwal - 6 years, 1 month ago

You person can you please tell which coaching aits you have joined for iit i am also an iit aspirant

Ram Sita - 3 years, 3 months ago

@Spandan Senapati , Can you help me figure out why is it so that when we do it with integration gives different answer. Actually, No one is active here.. .so i saw you solved the qs. Thats why I just tagged you. :D

Thanks

While doing with integration, I got 10.39.

Idk why

Md Zuhair - 3 years, 2 months ago

@Md Zuhair, when I did it with integration, I got 0. I know that conceptually, I 'm very weak at solving electric field problems but can you please help me find the correct equation for E in case of this equilateral triangle. What I did was

$dE=\frac{dq}{4\pi \epsilon_0(h^2+x^2+d^2)}$

$dE=\frac{\sigma\ dx\ da}{4\pi \epsilon_0(h^2+x^2+d^2)}$

$dE\cos\theta=\frac{\sigma\ dx\ da\times d}{4\pi \epsilon_0(h^2+x^2+d^2)^{\frac{3}{2}}}$

$E=\int^a_0\int^{\frac{a}{2}}_{\frac{-a}{2}}\frac{\sigma\times d\ dx\ da}{4\pi \epsilon_0(h^2+x^2+d^2)^{\frac{3}{2}}}$

$E=0$

where h=altitude of triangle=3a^2/4; a= side of the triangle

Shreyansh Mukhopadhyay - 3 years, 2 months ago

No no. Why will it be $h^2+x^2+d^2$ .

Check this image out

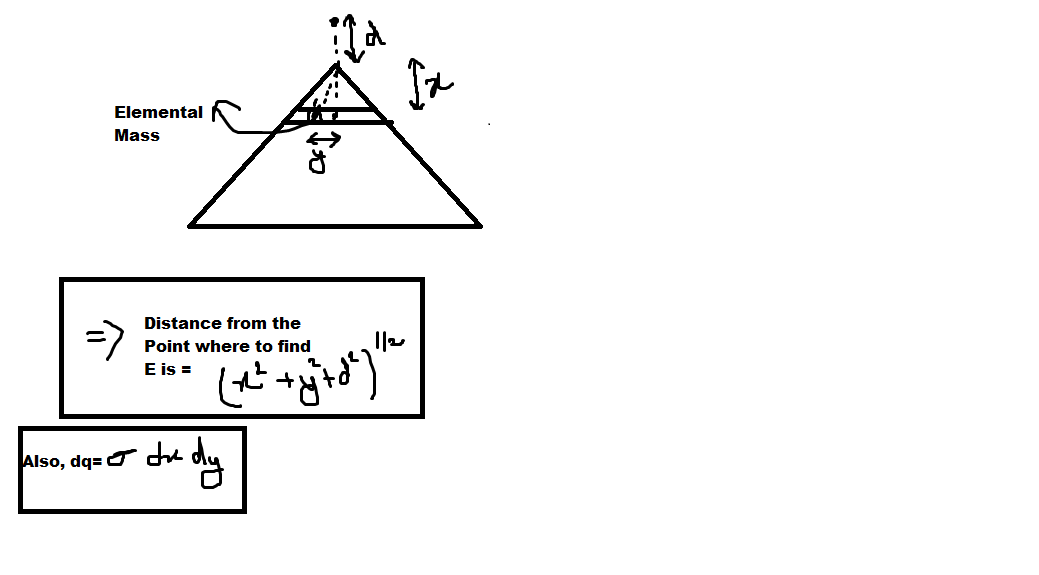
So our relation between, x and y will be obtained from similar triangles

$\dfrac{x}{y}= \dfrac{\sqrt{3}a/2}{\dfrac{a}{2}}$

$\implies y= \dfrac{x}{\sqrt{3}}$ .

So we can apply this y in our integral also.

So our Electric field equation will be

Wouldnt it be like this?

I may be wrong. Correct me if I am, And Thanks for your Response

Md Zuhair - 3 years, 2 months ago

@Md Zuhair – Thanks a lot for giving me the correct expression of E. And before looking at Ronak Agrawals solution I thought that the formula that he has used is valid only for circular disk. So is it true for any regular polygon?

By the way I think that in the final expression it would be dydx instead of dxdy.

Shreyansh Mukhopadhyay - 3 years, 2 months ago

@Shreyansh Mukhopadhyay – As we arr taking small elements of y in the strip x... we need to add up the y's first. So it will be dxdy. And I dont understand what you said above. Can you please elaborate?

Md Zuhair - 3 years, 2 months ago

@Md Zuhair – Actually seeing the diagram, it seems that you have interchanged x and y(May be I 'm wrong).

Anyways I meant that is the formula $\frac{\sigma}{2{\epsilon}_{0}}$ valid for any regular polygon /circle.

Shreyansh Mukhopadhyay - 3 years, 2 months ago

@Shreyansh Mukhopadhyay – Ya. I guess... As far as my knowledge goes. I wasn't also quite sure about it. If you know something like that pleas let me onow

Md Zuhair - 3 years, 2 months ago

@Shreyansh Mukhopadhyay – Hey good news!! Just integrated it and say the result came sigma/12e. So we are correct!!!

Md Zuhair - 3 years, 2 months ago

@Md Zuhair – Thats great and thanks a lot!

Shreyansh Mukhopadhyay - 3 years, 2 months ago

@Shreyansh Mukhopadhyay – Never mind. Your title seem to be of a Bengali person . Are you Bengali? I am bengali

Md Zuhair - 3 years, 2 months ago

@Md Zuhair – Yes I'm but I live in Chhattisgarh.

Shreyansh Mukhopadhyay - 3 years, 2 months ago

@Shreyansh Mukhopadhyay – So can you speak in Bengali?

Md Zuhair - 3 years, 2 months ago

@Md Zuhair – Yeah, very well.

Shreyansh Mukhopadhyay - 3 years, 2 months ago

Nice... Bhalo I tahole. Do you have WhatsApp?

Md Zuhair - 3 years, 2 months ago

@Md Zuhair – Yes, my mum's.

Shreyansh Mukhopadhyay - 3 years, 2 months ago

@Shreyansh Mukhopadhyay – https://brilliant.org/problems/lets-3d-ise-itmy-first-em-problem/?ref_id=1489713

Is the answer of this quite large... As lambda s unit isn't given

Md Zuhair - 3 years, 2 months ago

@Md Zuhair – $dE=\frac{dq}{4\pi\epsilon_0 R^2}$

Since $dq=\lambda_0\cos\theta R \ d\theta$

$dE\cos\phi=\frac{\lambda_0\cos\theta R z}{4\pi\epsilon_0 {(z^2+R^2)}^{\frac{3}{2}}} \ d\theta$

$E=\int^{2\pi}_0\frac{\lambda_0\cos\theta R z}{4\pi\epsilon_0 {(z^2+R^2)}^{\frac{3}{2}}}\ d\theta$

$E=0$

What wrong 'm I doing? Please give a hint.

Shreyansh Mukhopadhyay - 3 years, 2 months ago

@Shreyansh Mukhopadhyay – Do you know, that this question is a bit unique, Here vertical Electric field cuts out, but Horizontal one remains, as we know, with cos changes sign, You will see, The horizontal component remains. This is a hint

Md Zuhair - 3 years, 2 months ago

Electric fields due to different kinds of plates

The answer is 9.416.

1 solution

1 pending report

Vote up reports you agree with