Electric Flux Exercise (part 1)

Electricity and Magnetism Level pending

Two identical A ( − 1 , 0 , 0 ) A(-1,0,0) and B ( 1 , 0 , 0 ) B(1,0,0) particles of each charge q = 100 C q=100C are projected from the ring. Particle A is launced in x − z x-z with a speed v = 10 m s − 1 v=10ms^{-1} at an angle of 30 ° 30° from + x +x axis. Particle B is launched in x − z x-z with a speed of 20 m s − 1 20ms^{-1} at an angle of 60 ° 60° from − x -x axis.A ring is located in x − y x-y plane has the equation x 2 + y 2 = 1 x^{2} +y^{2} =1 If the electric flux through particle A A is ϕ A \phi_{A} at time and through particle B B is ϕ B \phi_{B} at t = 1 s e c t=1sec Type your answer as ( ϕ A + ϕ B ) × 10 (\phi_{A}+\phi_{B})×10 Details and Assumtions Take g = 10 m s − 2 g=10ms^{-2} in − Z -Z direction, ϵ 0 = 1 \epsilon_{0}=1 The answer is positive


The answer is 0.866.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Steven Chase
Apr 18, 2020

Particle A A makes no contribution to the flux, since it is located in the x y xy plane at t = 1 t = 1 . Compute the flux from particle B B at that time. 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
 
import math

# Constants

Num = 4000

deg = math.pi/180.0
R = 1.0

q = 100.0

e0 = 1.0
k = 1.0/(4.0*math.pi*e0)

g = 10.0

t = 1.0

#####################################

# Preliminary kinematic calculations

v0A = 10.0
thetaA = 30.0*deg

v0Ax = v0A*math.cos(thetaA)
v0Az = v0A*math.sin(thetaA)

v0B = 20.0
thetaB = 60.0*deg

v0Bx = -v0B*math.cos(thetaB)
v0Bz = v0B*math.sin(thetaB)

#####################################

# Determine charge positions at t = 1

yA = 0.0
yB = 0.0

xA = -1.0 + v0Ax*t
xB = 1.0 + v0Bx*t

zA = v0Az*t - 0.5*g*(t**2.0)
zB = v0Bz*t - 0.5*g*(t**2.0)

#####################################

# Print coordinates of two points
# Charge A makes no contribution to flux because zA = 0

#print "A coord"
#print xA
#print yA
#print zA

#print ""

#print "B coord"
#print xB
#print yB
#print zB

#print ""
#print ""

#####################################

phiB = 0.0

#####################################
#####################################
#####################################
#####################################

dr = R/Num
dtheta = 2.0*math.pi/Num

nx = 0.0
ny = 0.0
nz = -1.0

z = 0.0

r = 0.0

while r <= R:

    theta = 0.0

    while theta <= 2.0*math.pi:

        x = r*math.cos(theta)
        y = r*math.sin(theta)

        dS = r*dr*dtheta

        Dx = x - xB
        Dy = y - yB
        Dz = z - zB

        D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

        ux = Dx/D
        uy = Dy/D
        uz = Dz/D

        E = k*q/(D**2.0)

        Ex = E * ux
        Ey = E * uy
        Ez = E * uz

        dot = Ex*nx + Ey*ny + Ez*nz

        dphi = dot * dS

        phiB = phiB + dphi

        theta = theta + dtheta

    r = r + dr

################################################

print Num
print ""

print phiB
print (10.0*phiB)

################################################

#>>> 
#1000

#0.0866744927106
#0.866744927106
#>>> ================================ RESTART ================================
#>>> 
#2000

#0.0867644414956
#0.867644414956
#>>> ================================ RESTART ================================
#>>> 
#4000

#0.0867227095753
#0.867227095753
#>>>

1 Helpful 1 Interesting 1 Brilliant 0 Confused

@Steven Chase in your new question i am getting both I R 0 I_{R0} and I R ∞ I_{R∞} as 10 A 10A .

A Former Brilliant Member - 1 year, 1 month ago

Log in to reply

What about the sign (positive and negative)?

Steven Chase - 1 year, 1 month ago

Log in to reply

@Steven Chase I R 0 = 10 A I_{R0=10A} and I R ∞ = − 10 A I_{R∞=-10A}

A Former Brilliant Member - 1 year, 1 month ago

Log in to reply

@A Former Brilliant Member – Yes, that's right. By the way, could you double check your answer to the new electric field problem? Thanks for the dedication, too.

Steven Chase - 1 year, 1 month ago

Log in to reply

@Steven Chase – @Steven Chase Yes let me check it.

A Former Brilliant Member - 1 year, 1 month ago

Log in to reply

@A Former Brilliant Member – @Steven Chase I have corrected it.

A Former Brilliant Member - 1 year, 1 month ago

@Steven Chase – @Steven Chase Hii. The cases and deaths are increasing in such a fast way. I just want to know the atmosphere around your house? Did you go outside for anything??

A Former Brilliant Member - 1 year, 1 month ago

Log in to reply

@A Former Brilliant Member – @Steven Chase Are you free nowl I want to ask 2-3 conceptual doubt regrading gauss law?? (related to theory)

A Former Brilliant Member - 1 year, 1 month ago

Log in to reply

@A Former Brilliant Member – Sure, what are they?

Steven Chase - 1 year, 1 month ago

Log in to reply

@Steven Chase – @Steven Chase 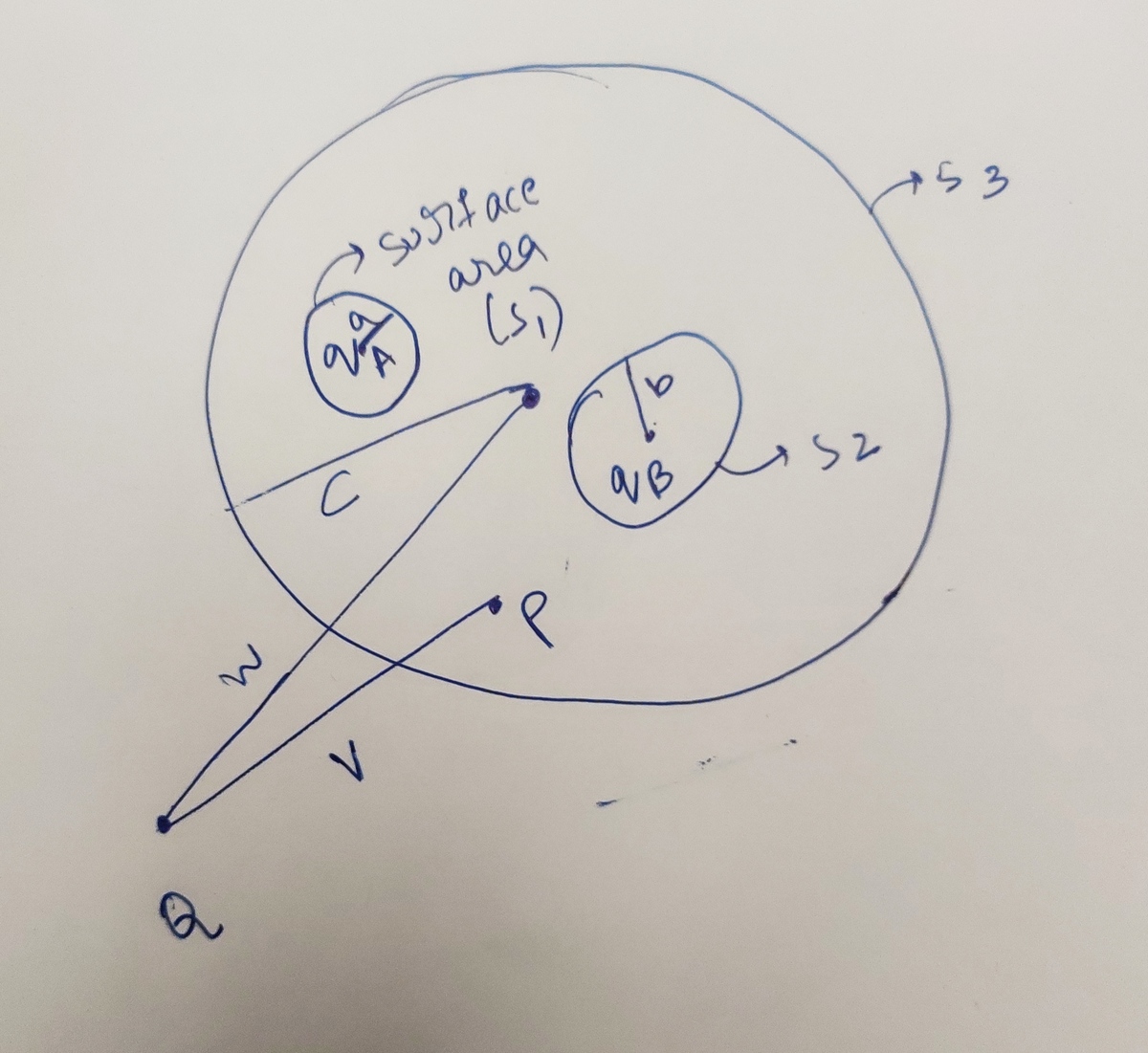Find the surface charge density(sigma) on all three surface( S 1 , S 2 , S 3 S_{1}, S_{2}, S_{3} ?

If there is lack of some information you can attach your information by yourself also.

A Former Brilliant Member - 1 year, 1 month ago

Log in to reply

@A Former Brilliant Member – Why would there be a surface charge density? Is this some sort of material?

Steven Chase - 1 year, 1 month ago

Log in to reply

@Steven Chase – 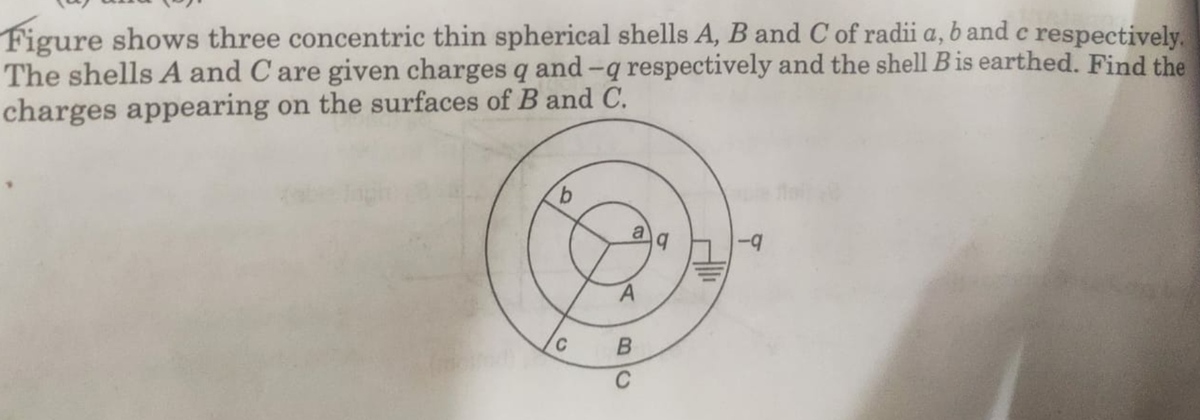This one?

A Former Brilliant Member - 1 year, 1 month ago

Log in to reply

@A Former Brilliant Member – There are solutions to these online:

https://doubtnut.com/question-answer-physics/figure-shows-three-concentric-thin-spherical-shells-a-b-and-c-of-radii-a-b-and-c-respectively-the-sh-9726154

Steven Chase - 1 year, 1 month ago

Log in to reply

@Steven Chase – @Steven Chase Did you use doubtnut also? It's a Hindi app. Did you speak hindi also???

A Former Brilliant Member - 1 year, 1 month ago

Log in to reply

@A Former Brilliant Member – No, I just typed the problem text into Google

Steven Chase - 1 year, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...