Electro-mechanics (Part 2)
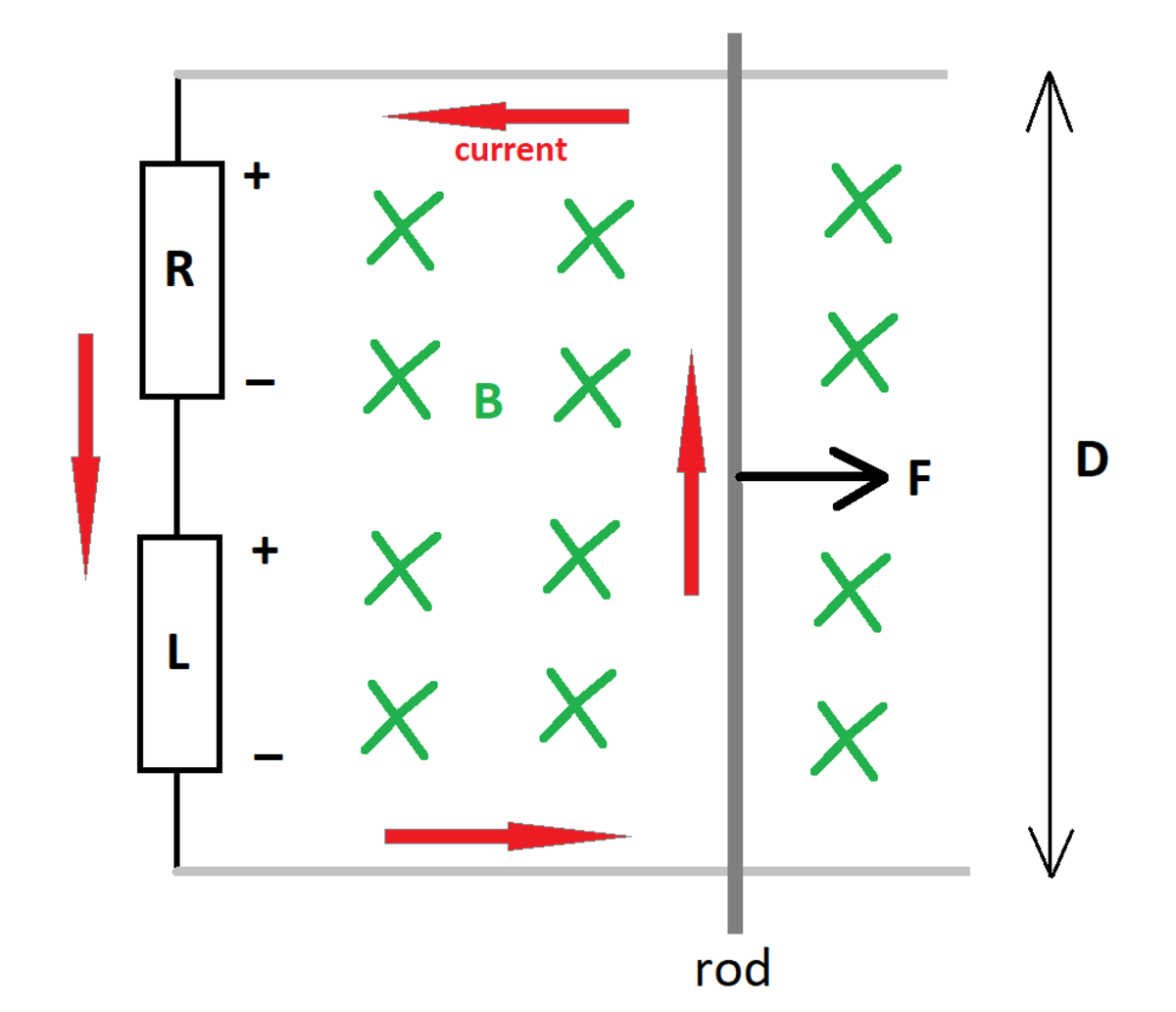
A conducting rod of mass m slides along a pair of conducting rails which are separated by a distance D . The rod is pulled rightward by a constant force F . A series combination of a resistor ( R ) and an inductor ( L ) completes the circuit. There is an ambient magnetic flux density B which points into the page.
Initially, the rod has zero speed and there is no current in the circuit. Let the velocity be a signed number, with a positive sign denoting rightward motion (in the direction of the force) and a negative sign denoting leftward motion.
What is the minimum velocity value over all time?
Details and Assumptions:
1)
m
=
1
2)
D
=
2
3)
F
=
1
0
4)
R
=
1
5)
L
=
1
6)
B
=
5
7)
There is no gravity
8)
Neglect the magnetic field contributions from the rails
The answer is -0.688.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Alak Bhattacharya Did you solve this this question without any mathematical tool??
Consider the given situation at a general instant of time t . Let the current through the circuit be I and the velocity of the rail as it moves to the right be v . Applying Kirchoff's voltage law gives:
− B D v + I R + L I ˙ = 0 … ( 1 )
Here E = B D v is the magnitude of induced voltage due to electromagnetic induction.
Applying Newton's second law to the rail gives:
F − I D B = m v ˙ … ( 2 )
Re-arranging the above equations in a matrix form gives:
[ I ˙ v ˙ ] = [ − R / L − B D / m B D / L 0 ] [ I v ] + [ 0 1 / m ] F
Let:
x = [ I v ]
Substituting all values:
x ˙ = [ − 1 − 1 0 1 0 0 ] x + [ 0 1 0 ]
Initial conditions:
x ( 0 ) = [ 0 0 ]
For the sake of convenience, I solved this numerically beyond this point. A plot of velocity vs. time is as such:
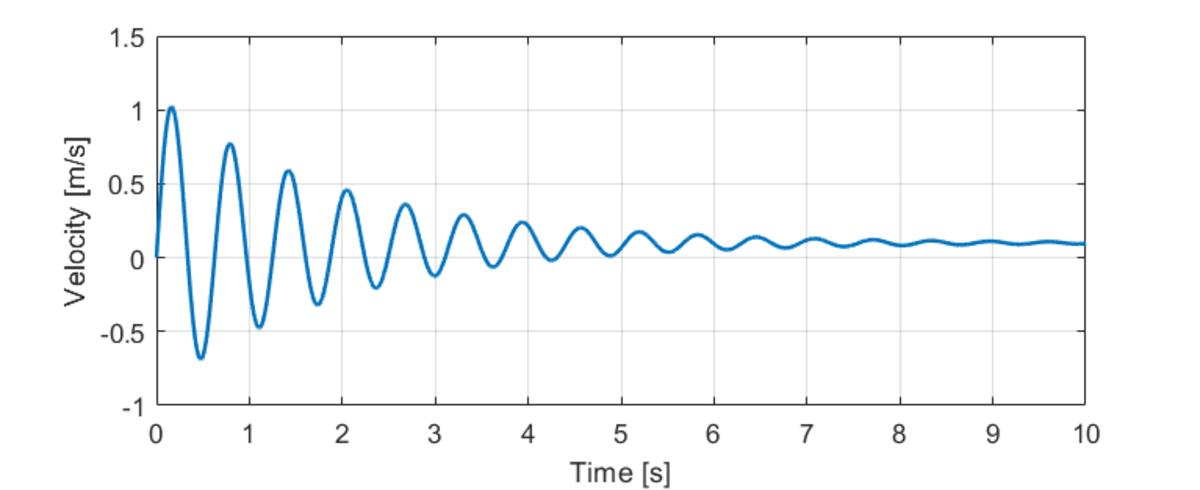
One can see that the rod moves left-ward and rightward and this oscillation is damped until it settles to its steady-state value of 0.1.
@Karan Chatrath Nice solution. I just upvoted it . BTW can you find Self energy of Hollow hemisphere?
Log in to reply
You requested such a problem before. Refer to the solution here, please
https://brilliant.org/problems/spherical-shell-binding-energy/
Log in to reply
@Karan Chatrath Sir mai Hollow hemisphere puch rha. Aapne jo question diya vo spherical shell hai??
Log in to reply
@A Former Brilliant Member – Oh, I misread your question. I will attempt this later.
@Karan Chatrath at the(last step) initial conditions of your solution, I think there should be 10.correct me if I am wrong.
This is an example of damped oscillation driven by a constant force. (A case of overdamping).
The current flowing through the circuit is given by the equation
R i + L d t d i = B D v ⟹ R d t d i + L d t 2 d 2 i = B D d t d v .
The equation of motion of the rod is given by
F − i D B = m d t d v .
Combining these two, we get
d t 2 d 2 I + 2 b d t d I + ω 0 2 I = 0 , where
I = i − B D F , b = 2 L R , ω 0 = m L B D .
Solving this equation we get
i = B D F + A e − b t sin ( ω t + α ) , where A , α are constants of integration to be determined, and ω = ω 0 2 − b 2 .
Substituting values, we get
i = 1 + A e − 2 t sin ( 2 3 9 9 t + α ) , v = i + d t d i = 1 0 1 ( 1 + 1 0 A e − 2 t sin ( ω t + α + tan − 1 2 ω ) ) .
Initial conditions yield
A sin α = − 1 , 1 0 A sin ( α + tan − 1 2 ω ) = − 1 ⟹ A = 3 9 9 2 0 , α = tan − 1 2 ω .
Hence,
v = 1 0 1 ( 1 + 3 9 9 2 0 0 e − 2 t sin ( 2 3 9 9 t − tan − 1 1 9 9 3 9 9 ) ) .
Velocity will be minimum when the sine function in it's expression will be − 1 . Hence
t = 3 9 9 2 ( 2 3 π + tan − 1 ( 1 9 9 3 9 9 ) )
Then v m i n = 1 0 1 ( 1 − 3 9 9 2 0 0 e − 2 t ) ≈ − 0 . 6 8 6 8 8 6 .