Electromagnetically induced.
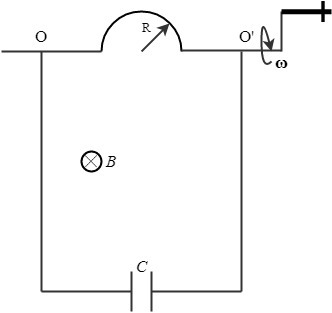
A conducting rod is bent in the shape of a semicircle of radius and the straight parts along the ends of the diameter of the semicircle are passed through fixed, smooth conducting rings and A capacitor having capacitance is connected to the rings with the help of ideal wires. The system is placed in a uniform magnetic field of strength such that the axis of rotation is perpendicular to the direction of the magnetic field.
Initially, the plane of the semicircle was normal to the direction of the field. The semicircle is now rotated about the axis with a constant angular velocity of . Neglect any resistance and self-inductance of the circuit.
The power required to keep the semicircle rotating with a constant angular velocity of can be expressed as where letters from to are positive integers (not necessarily coprime).
Find .
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Loop area:
A = A 0 + 2 π R 2 c o s ( ω t )
Flux Linkage:
λ = B A = B A 0 + 2 π B R 2 c o s ( ω t )
Voltage across capacitor (assuming no resistance or self-inductance in circuit):
v C = λ ˙ = − 2 π ω B R 2 s i n ( ω t )
Current through capacitor:
i C = C v C ˙ = − 2 π C ω 2 B R 2 c o s ( ω t )
Power associated with capacitor:
P C = v C i C = 4 π 2 ω 3 C B 2 R 4 s i n ( ω t ) c o s ( ω t ) = 8 π 2 ω 3 C B 2 R 4 s i n ( 2 ω t )
The parameters therefore sum to 2 0