Electron's U-Turn
Consider an infinitely long wire having a circular cross-section of radius
2
m
. The wire is placed along the
Y
-axis and a current of
0
.
1
2
A
flows uniformly throughout its cross-section along the positive
Y
direction (The distribution is actually irrelevant). An electron is projected from
(
2
,
0
,
0
)
the surface of this long wire with a speed 0f
1
0
0
0
i
^
m
/
s
.Compute the maximum
x
-coordinate of the particle while it is in motion. Assume that the motion of the electron is affected only by the magnetic field
generated by the wire.
Note:
i
^
vector is along
x
direction
1
)
m
e
=
1
.
7
5
8
8
2
0
×
1
0
1
1
C
k
g
−
1
2
)
μ
0
=
4
π
×
1
0
−
7
N
A
−
2
The problem is not original.
The answer is 2.534.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Karan Chatrath Proposal is accepted. And this problem is edited according to your wish.. I think that for that question Electron leads parabolic Track which you reported, I said that @Steven Chase has solved it, which might feel you sad. Therefore you are saying that it is clear for others but not for me,so sorry for that. N o P r o b l e m . From next time I will state the problem in such a tremendous way that, even aliens wouldn't find any ambiguity while solving the problems. Hope we have a good relationship further. C H E E R S !
Log in to reply
Hi, thanks for understanding. Really appreciate it. And no, at no point did I feel bad.
This time, I must apologise as I realise a mistake I have made in the problem statement. Updated statement.
Consider an infinitely long wire having a circular cross-section of radius 2. The wire is placed along the Y-axis and a current of 0 . 1 2 A flows uniformly throughout its cross-section along the positive Y direction. An electron is projected from the point ( 2 , 0 , 0 ) with a velocity of v o = 1 0 0 0 i ^ m / s . Compute the maximum x-coordinate of the particle while it is in motion. Assume that the motion of the electron is affected only by the magnetic field generated by the wire.
Note: i ^ is a unit vector along the positive X-axis.
I also have another suggestion. I noticed that your next problem is taken from I.E Irodov. When you post a non-original problem, make a mention of the source and the fact that the problem is not original. These are good practices.
Log in to reply
@Karan Chatrath
As you have helped me so much.
I
w
i
l
l
f
o
r
g
i
v
e
y
o
u
r
e
v
e
r
y
m
i
s
t
a
k
e
I have corrected the problem.
In the last 3rd line of this solution(L.H.S), you missed something useful.
Log in to reply
@A Former Brilliant Member – Nice catch! Corrected. Thank you
@A Former Brilliant Member – Also, your updated problem statement is still not okay. You need to mention the point of projection. Refer to my previous comment where I re-stated the problem.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
Sir my
9
0
%
−
9
5
%
problems are original.
My intention is not to post original problems my intention is to post
G
o
o
d
problems.
Log in to reply
@A Former Brilliant Member – Okay, noted.
But I was referring to this current problem's statement. The point about acknowledging sources was a passing mention. Please update your problem statement to the following for correctness.
Consider an infinitely long wire having a circular cross-section of radius 2. The wire is placed along the Y-axis and a current of 0 . 1 2 A flows uniformly throughout its cross-section along the positive Y direction. An electron is projected from the point ( 2 , 0 , 0 ) with a velocity of v o = 1 0 0 0 i ^ m / s . Compute the maximum x-coordinate of the particle while it is in motion. Assume that the motion of the electron is affected only by the magnetic field generated by the wire.
Log in to reply
@Karan Chatrath – @Karan Chatrath Now please delete by report
Log in to reply
@A Former Brilliant Member – I want to delete, but it is still not okay. You have mentioned the point of projection and initial velocity so now there is no need to mention that the projection is radially outward. That is redundant information. Please take the suggested problem statement as I have typed it. I will delete the report as soon as the edit is made.
Another point about clear problem statements is that they do not contain redundant information.
Log in to reply
@Karan Chatrath – @Karan Chatrath Remove that upvote of Alak Bhattacharya also.
Log in to reply
@A Former Brilliant Member – I have deleted the report as the problem is comparatively clearer than what it was, but the statement is still not okay if you ask me. See the exact statement that I posted a few minutes back and use that, is what I suggest, again.
@A Former Brilliant Member – @Karan Chatrath Sometimes I have noticed that 9 0 % problems of @Steven Chase are good ,but 9 % − 1 0 % problems needs only V E R Y − H A R D − M A T H E M A T I C S Which are tedious and leads to timewaste also. But overall I like his problems. Now you promise me you will not tell this to @Steven Chase . If you tell then he will scold me.
@Karan Chatrath Capacitor exercise part3 is corrected. Thanks
Because of the confusing statement, I could not answer the problem correctly, and lost the chance to post a solution. So I wish to post it here. Since at start, the electron moves radially outwards and the magnetic induction is directed tangentially to the wire, the initial velocity of the electron has no component along the direction of magnetic induction. Let the axis of the wire be along y -axis and the magnetic induction be along the z -axis. Force acting on the electron when it is at a distance r from the axis of the wire is F = e v × B ⟹ d t d v x = 2 π m r μ 0 e I v y , d t d v y = − 2 π m r μ 0 e I v x , d t d v z = 0 ⟹ v z = 0 .
So d t d v = − ( d t d v x ) 2 + ( d t d v y ) 2 = − 2 π m μ 0 e I r v ⟹ v 0 = 2 π m μ 0 e I ln ( a r m a x ) ⟹ r m a x = a e μ 0 e I 2 π m v 0 , where a is the radius of cross section of the wire, v 0 is the initial velocity of the electron, and r m a x is the maximum distance of the electron from the axis of the wire.
Nice problem. I solved by running a numerical simulation through time. Code is attached, with comments:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 |
|
@Steven Chase BTW Solving it analytically will be a pure fun .
Log in to reply
I'm surprised it's possible, given that the field magnitude is varying with distance from the axis
Log in to reply
@Steven Chase I have solved it analytically. But I am expecting that @karan sir will post analytically . Therefore I am not posting my solution. BTW I have made a question that we have a quadrilateral of all unequal sides at each corner a particle is placed. All have different charge. At each time I I separate each particle from the quadrilateral. Now I have 4 cases. Now the question is that if I pick a random case what will be average loss in potential energy of system . Will it be a good problem?
@Steven Chase a new one is uploaded have a look.
Log in to reply
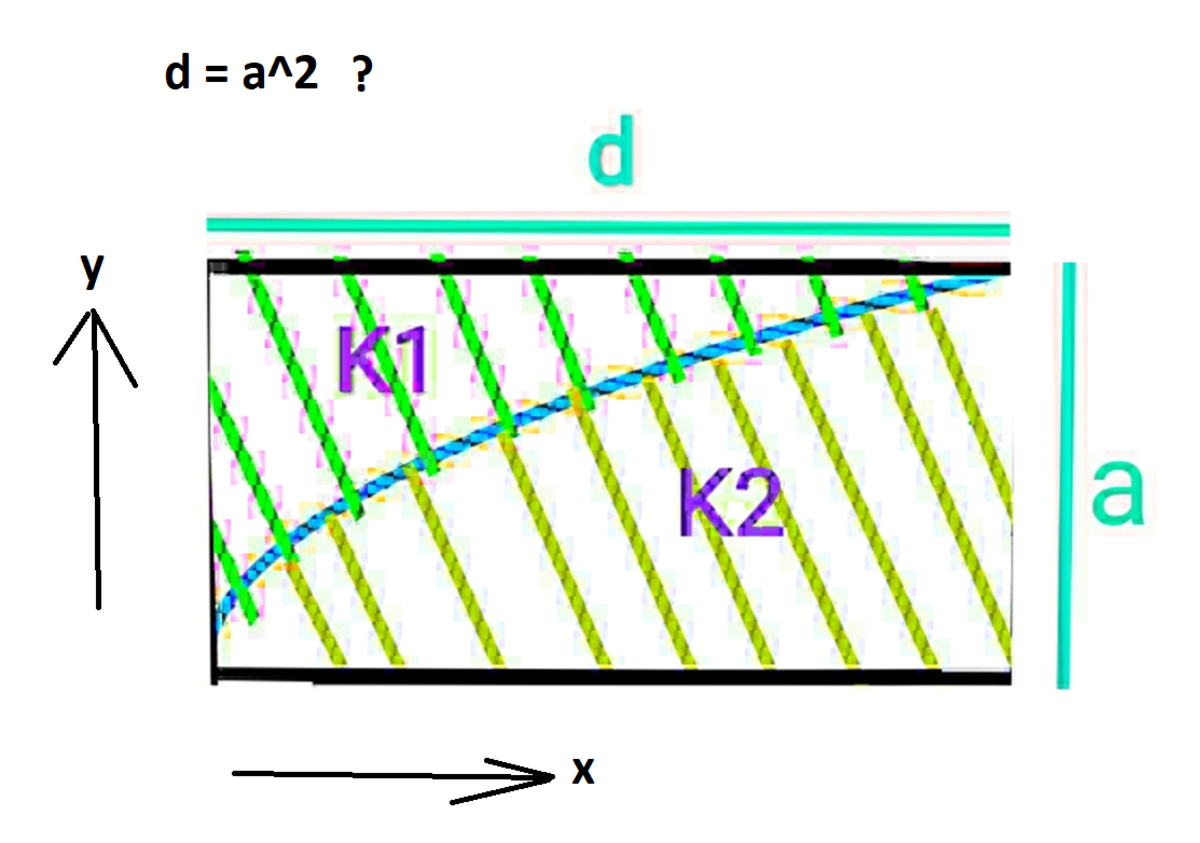
@A Former Brilliant Member – That looks like a fun one. My geometrical interpretation is summarized by the image below. But the equality condition doesn't hold, so how do we resolve that?
Log in to reply
@Steven Chase – @Steven Chase why that equation doesn't hold.?
Log in to reply
@A Former Brilliant Member – The numerical values for d and a don't satisfy that equation
Log in to reply
@Steven Chase – @Steven Chase OH yeah! Come after 10 min . I will change it
@Steven Chase – @Steven Chase Did you use code or solve Anaylitically??
Log in to reply
@A Former Brilliant Member – I haven't solved yet
Log in to reply
@Steven Chase
–
@Steven Chase
I am getting stuck. When I put
a
=
1
0
that d becomes
1
0
0
And at the top I have written that
d
<
<
a
Log in to reply
@A Former Brilliant Member – @Steven which contradicts
Log in to reply
@A Former Brilliant Member – You could say something like "assume that the standard capacitance formula holds"
Log in to reply
@Steven Chase – @Steven Chase I have deleted and reposted with correct answer.Now you can go and rock. BTW did you notice that wrong problem also has one solver. Haha
Log in to reply
@A Former Brilliant Member – I attempted the problem, and my answer was not accepted. For every d y , we have two infinitesimal capacitances in series ( d C 1 , d C 2 ) . And then the equivalent infinitesimal capacitance (from those two) is added to a running sum for the total capacitance. The equivalent infinitesimal capacitance is d C 1 + d C 2 d C 1 d C 2
Log in to reply
@Steven Chase – @Steven Chase Yes after this??
Log in to reply
@A Former Brilliant Member – @Steven Chase Share your approach till end.
Log in to reply
@A Former Brilliant Member – That is the approach
Log in to reply
@Steven Chase – @Steven Chase after equivalent infinitesimal Capacitance what did you have done??
Log in to reply
@A Former Brilliant Member – Add it to the running sum for the total capacitance, because it is in parallel with the other contributions for the other d y elements
Log in to reply
@Steven Chase – @Steven Yes it's correct
Log in to reply
@A Former Brilliant Member
–
@Steven Chase
This is my whole approach
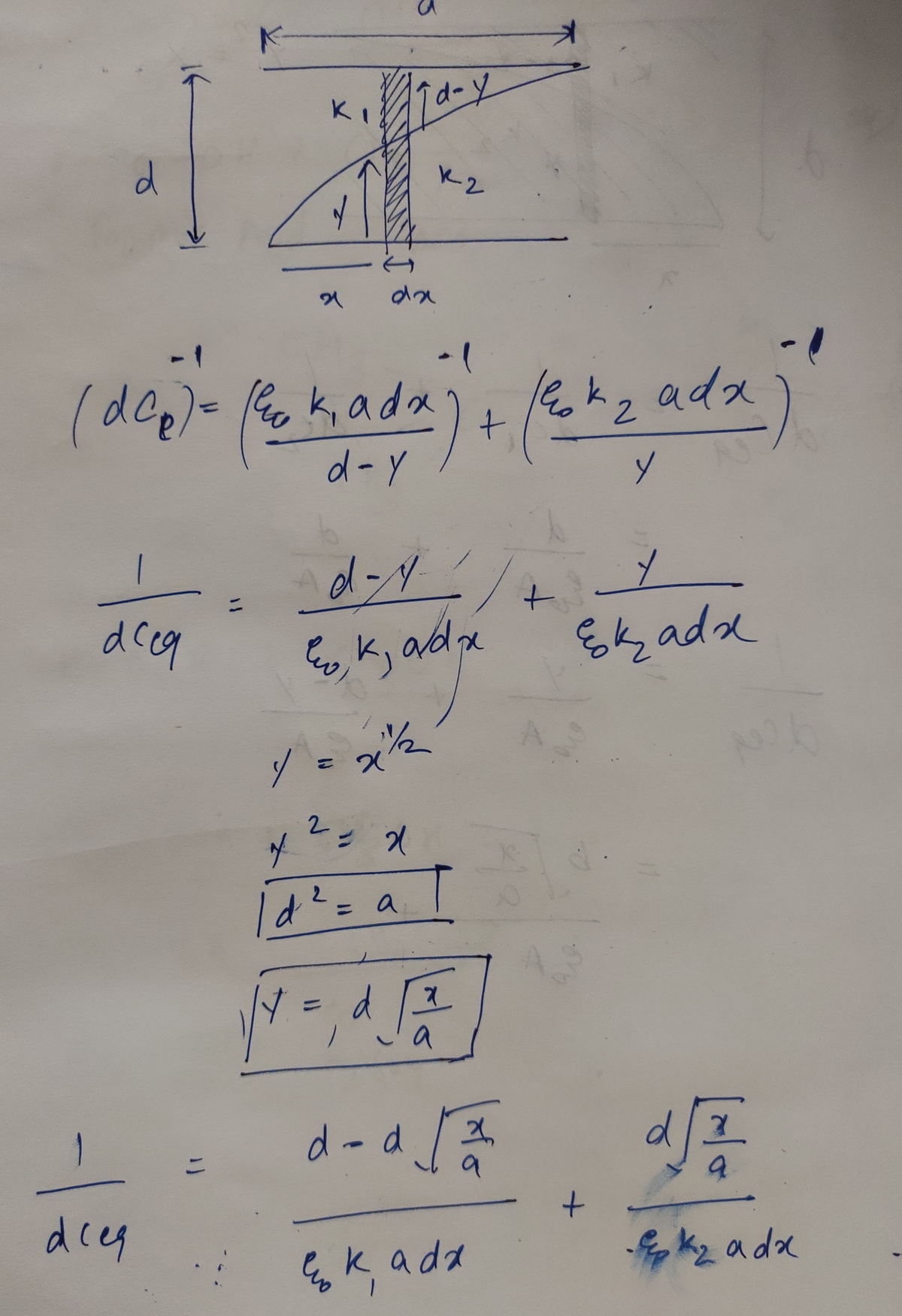
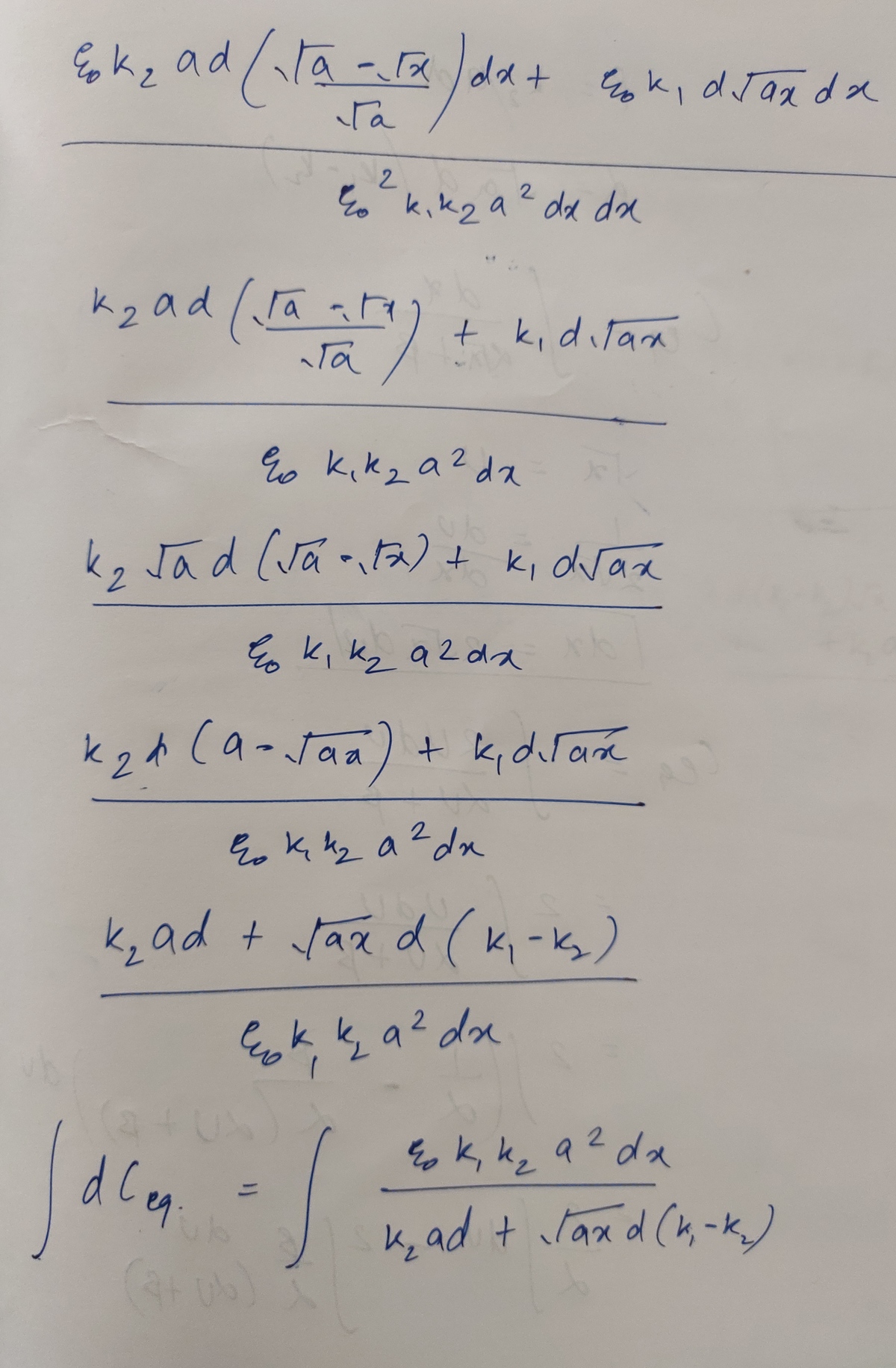
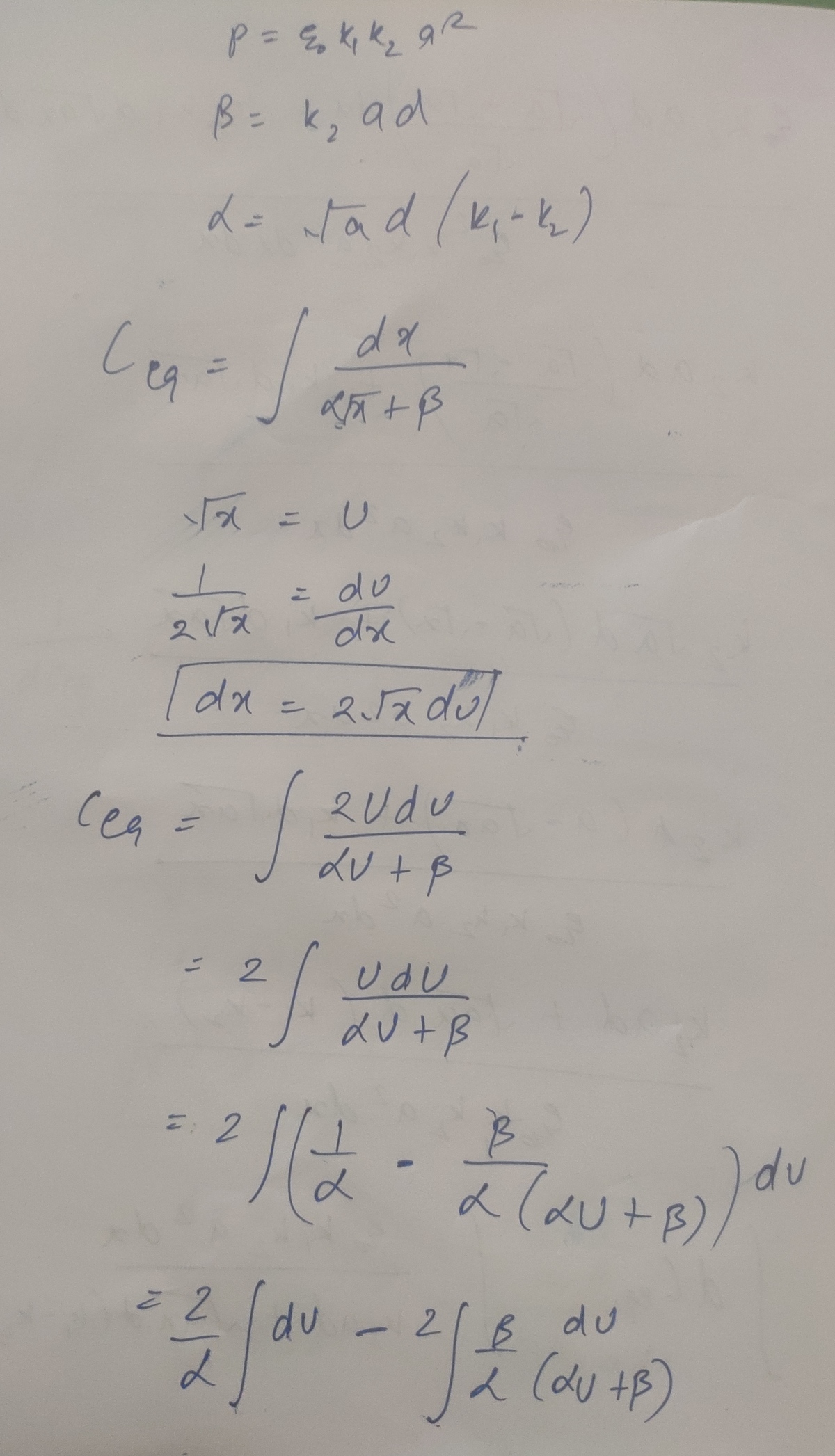
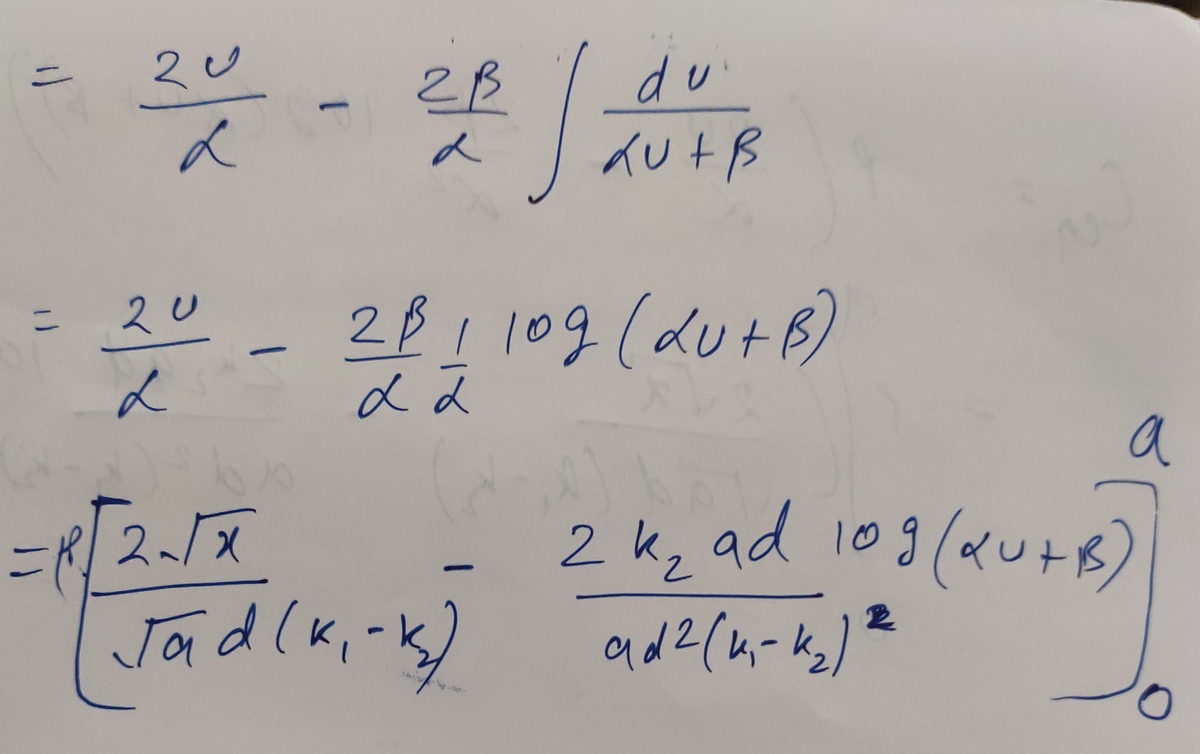

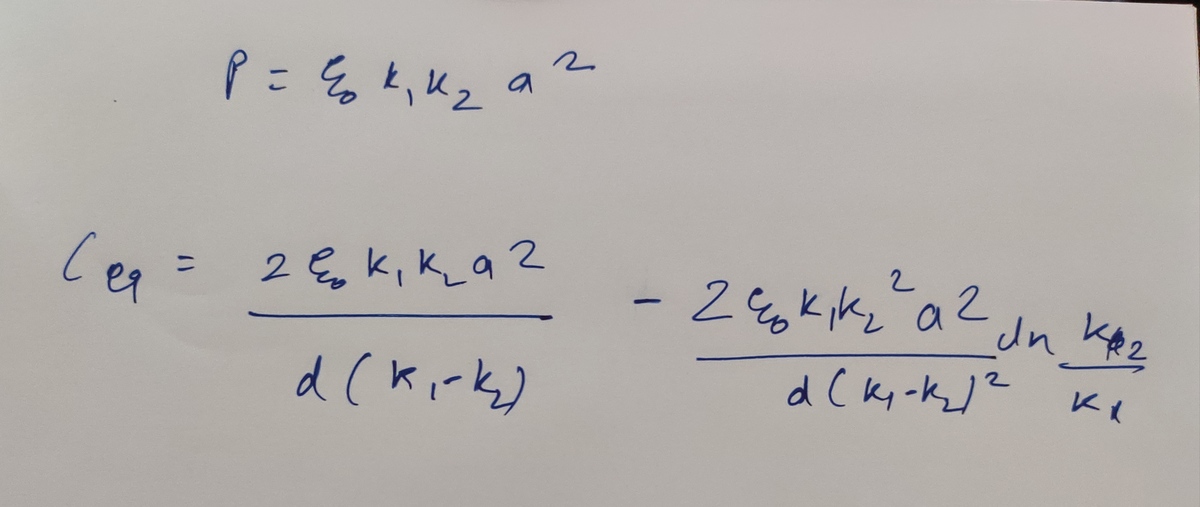
For the cap problem, the parameter a is associated with the y direction. Looks like you have it swapped in the solution
Log in to reply
@Steven Chase Mark the error with pen and show me
Log in to reply
@A Former Brilliant Member – Just compare your drawing in the solution with the drawing in the problem
Log in to reply
@Steven Chase – @Steven Chase it's already there . a .
Log in to reply
@A Former Brilliant Member
–
@Steven Chase
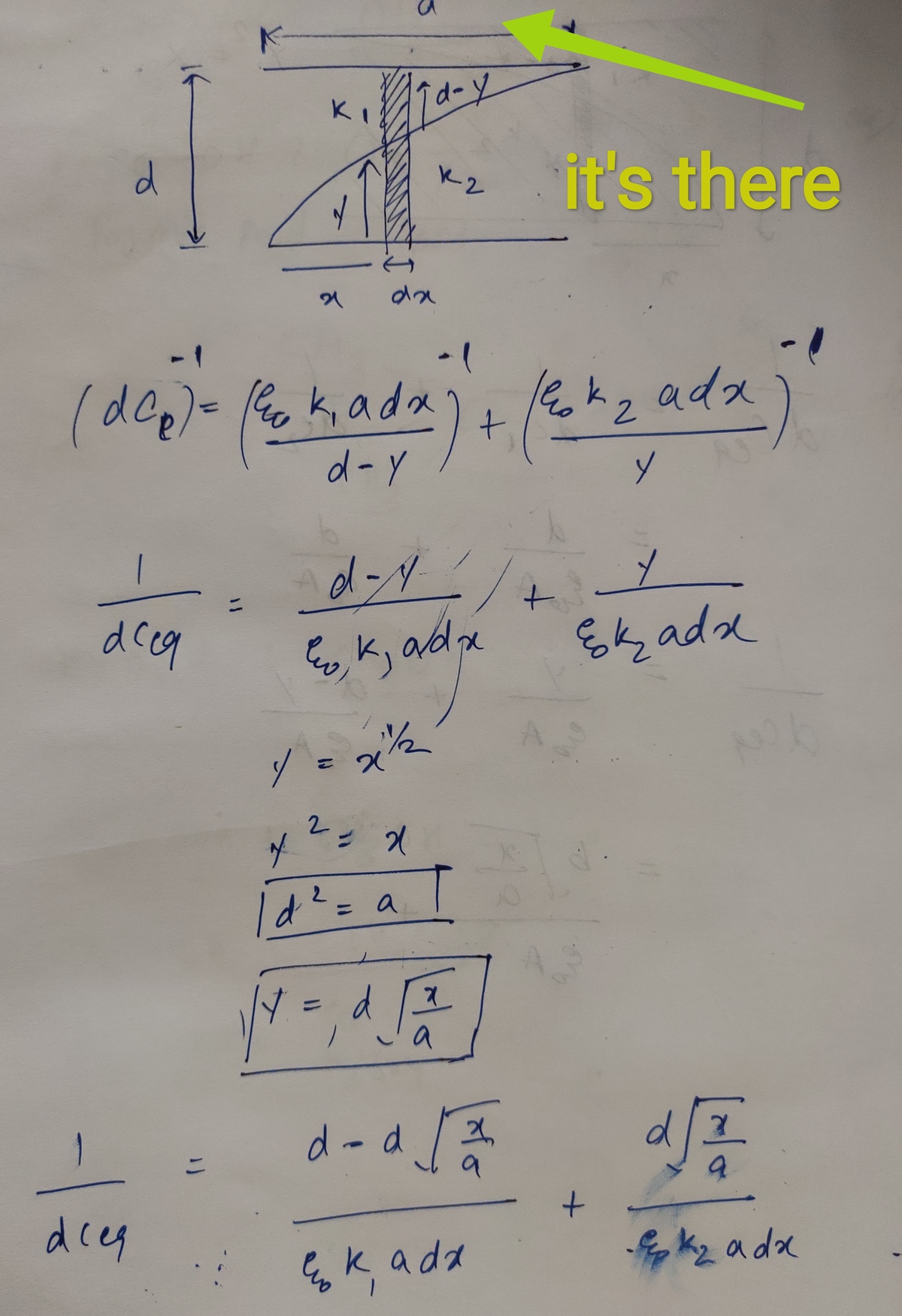
@Steven Chase Now I have replaced d with a. That mistake made me laugh. Now everything is correct. Can you find mistake in my Solution???
Log in to reply
@A Former Brilliant Member – Do the plates have dimension d or a?
Log in to reply
@Steven Chase – @Steven Chase they are square parallel plates of side a and distance between them is d .
Log in to reply
@A Former Brilliant Member – Ok, I'll try to solve again
Log in to reply
@Steven Chase – Are you going to swap the numerical values of a and d as well?
Log in to reply
@Steven Chase
–
@Steven Chase
I have changed the numerical vaules as well.
Did my solution is correct for average electric field

@Steven Chase – A charge is placed in a unit circle(parallel to xy) in random way. Find the average electric field at (2,,0))
Log in to reply
@A Former Brilliant Member – Looks right. Be sure to mention that you want the average field magnitude
@Neeraj Anand Badgujar @Steven Chase
Okay, after a lot of struggle, here it is:
Consider a long wire of circular cross-section area of radius 2 placed along the Y-axis. The electron is projected from the point ( 2 , 0 , 0 with an initial velocity of v o = v o i ^ = 1 0 0 0 i ^ . The current flowing through the wire is along the positive Y direction.
The magnetic field at any general point in space is:
B = − 2 π x μ o I k ^
At any general instant of time, let the velocity of the particle be:
V = v x i ^ + v y j ^
Applying Newton's second law:
m a = − e ( V × B )
Simplifying gives:
x ¨ = ( 2 π m μ o I e ) x y ˙ y ¨ = − ( 2 π m μ o I e ) x x ˙
Let:
A = 2 π m μ o I e
This gives:
d t d v x = x A v y d t d v y = − x A v x
Diving both equations above gives:
d v y d v x = − v x v y ⟹ v x d v x = − v y d v y
Integrating and applying initial conditions gives:
v x 2 + v y 2 = v o 2
This means that the speed of the particle is constant. Initially v y = 0 and we need to find the x-coordinate of the particle when v x becomes zero, as that would indicate a 'turning point'.
Using this intuition in the following equation:
d t d v y = − x A v x = − x A d t d x ⟹ d v y = − x A d x
Recognising that as x increases, the y-coordinate decreases. To ensure this, an additional negative sign is introduced above which transforms the ODE to:
d v y = − x A d x
Integrating:
∫ 0 − v o d v y = A ∫ 2 x o x d x
⟹ A v o = ln ( 2 x o )
⟹ x o = 2 e v o / A
I have reservations about the problem statement which I considered to be very misleading. This took me down a path where I unnecessarily over-complicated the problem.
The statement: 'From the surface of a round wire of radius 2m...' made me imagine that the wire is actually bent into the shape of a circular ring and that the wire has a negligible cross-section area. This confused me. I do not like poorly worded problems. Now I realise that others may find it easy to understand, but I am not one of those others, unfortunately. I require a great deal of clarity in statements.
I propose the following problem statement.
'Consider an infinitely long wire having a circular cross-section of radius 2. The wire is placed along the Y-axis and a current of 0 . 1 2 A flows uniformly throughout its cross-section along the positive Y direction (The distribution is actually irrelevant). An electron is projected from the surface of this long wire with a speed 0f 1000 m/s and its direction of projection is radially outward. Compute the maximum x-coordinate of the particle while it is in motion. Assume that the motion of the electron is affected only by the magnetic field generated by the wire.'
It would also help if you supplemented your problem statements with diagrams. I humbly re-iterate that you need to work on making your problem statements clearer. It may be clear to others but not for me. Thank you for understanding. I say this because I enjoy solving your problems and I wish to continue doing so.