Electrostatics Equilibrium Problem.
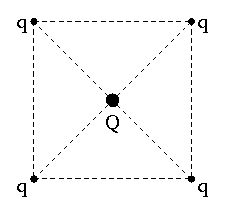 It is required to hold four equal point charges
each in equilibrium at the corners of a square. Find the charge
in Coulombs
,
, that will do this if kept at the center of the square.
It is required to hold four equal point charges
each in equilibrium at the corners of a square. Find the charge
in Coulombs
,
, that will do this if kept at the center of the square.
Details and Assumptions:
The answer is -0.957.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A s w e k n o w , F = C r 2 q 1 q 2 l e t l e n g t h o f s i d e i s a N e t f o r c e o n a n y o f + q w i l l b e , F = 2 C a 2 q 2 c o s 4 5 o + C ( a 2 ) 2 q 2 + C ( 2 a ) 2 Q q ⇒ F = 2 2 2 + 1 C a 2 q 2 + 2 C a 2 Q q ( o u t w o r d a l o n g d i a g o n a l ) f o r b a l a n c e F = 0 ⇒ Q = − 4 2 2 + 1 q ⇒ Q = − 0 . 9 5 7 q