Ellipse and Particle
A Ellipse is placed in
plane of equation with
as origin
Now, I am taking a random point inside ellipse like
Then , I am projecting a particle of mass
from that
with a velocity of
from positive
axis by an angle of
in the
plane.
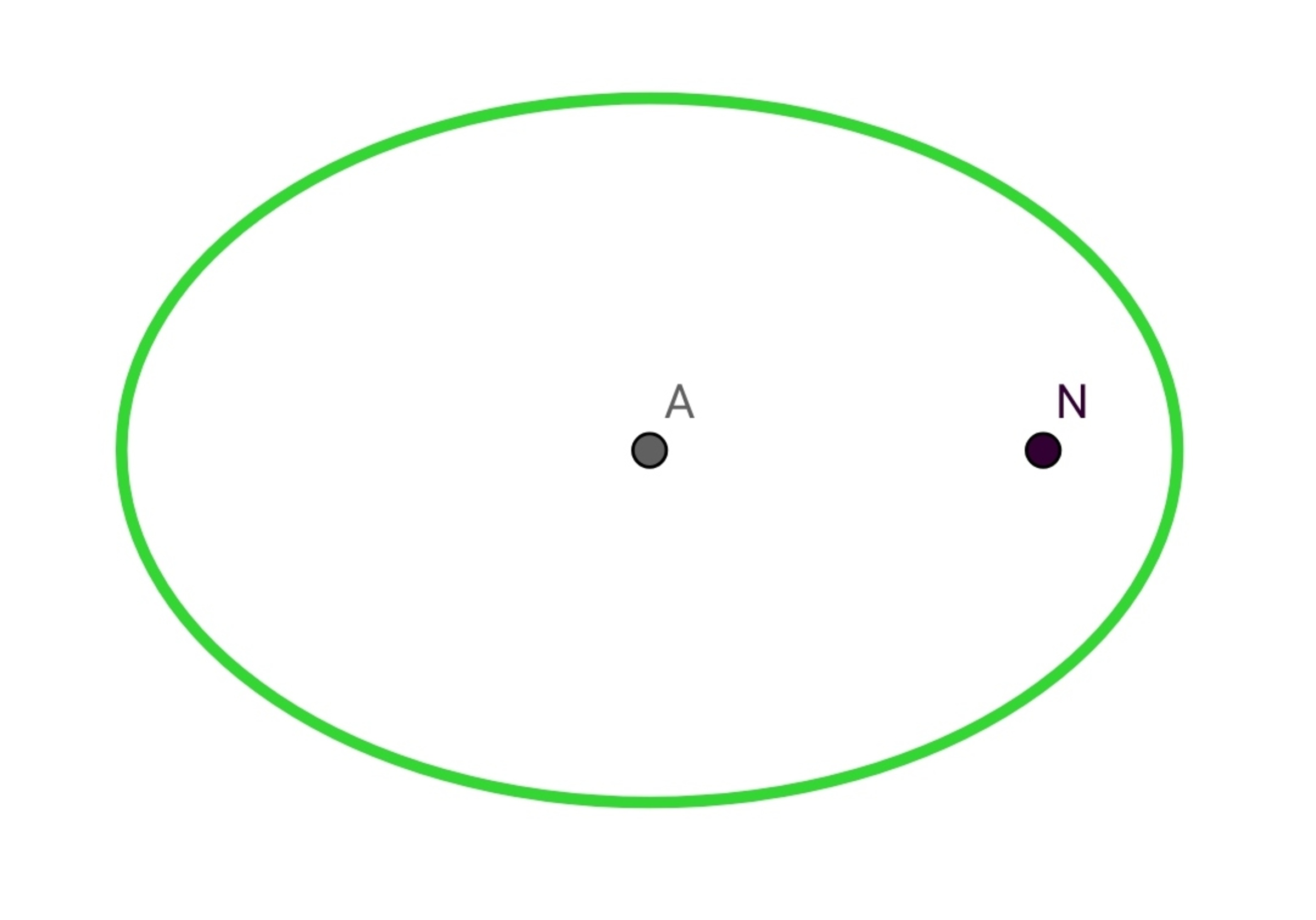
Find the minimum time taken by the particle to reach
again.
Details and Assumptions
1)
2)
3)
(
)where
is Euler's number ,
(
These approximations may help you
)
.
4)
Friction coefficient of plane is
5)
Consider that the particle will remain inside that area covered by ellipse.
6)
Friction is only responsible for loss in velocity of particle.
7)
Consider everything in SI units.
8)
Remember that angle of incidence is equal to angle of reflection.
9)
Gravity is acting downwards , perpendicular to
plane ,
The answer is 0.12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
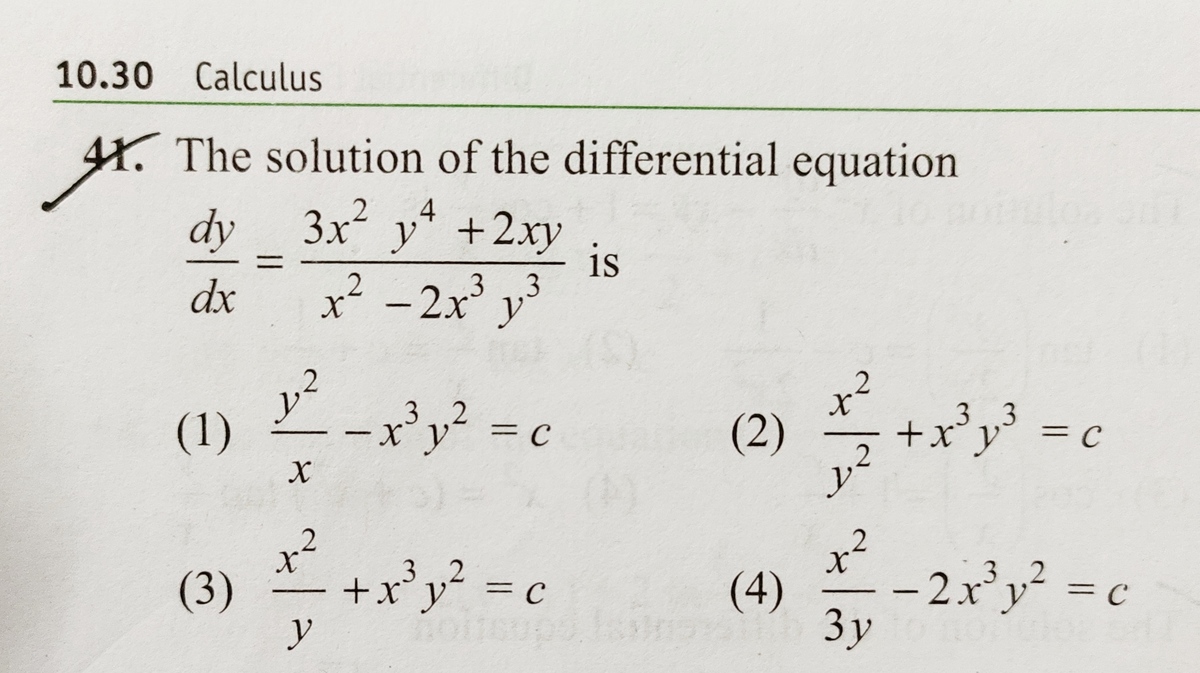
A ray leaving the focus of an ellipse will travel a distance 2 a before arriving at the other focus (where a = 3 is the semi-major axis length). On its way to the other focus, it reflects off of the ellipse. Therefore, the particle will travel a distance 4 a before returning to its starting point. The acceleration of the particle is v ˙ = − μ g , and the initial speed v 0 = 1 0 0 . We have the following equation:
4 a = v 0 t f + 2 1 v ˙ t f 2
Solving the quadratic and choosing the appropriate root results in t f ≈ 0 . 1 2 . It should be noted that the presence of friction makes almost no difference to the result.