Ellipse Sandwich
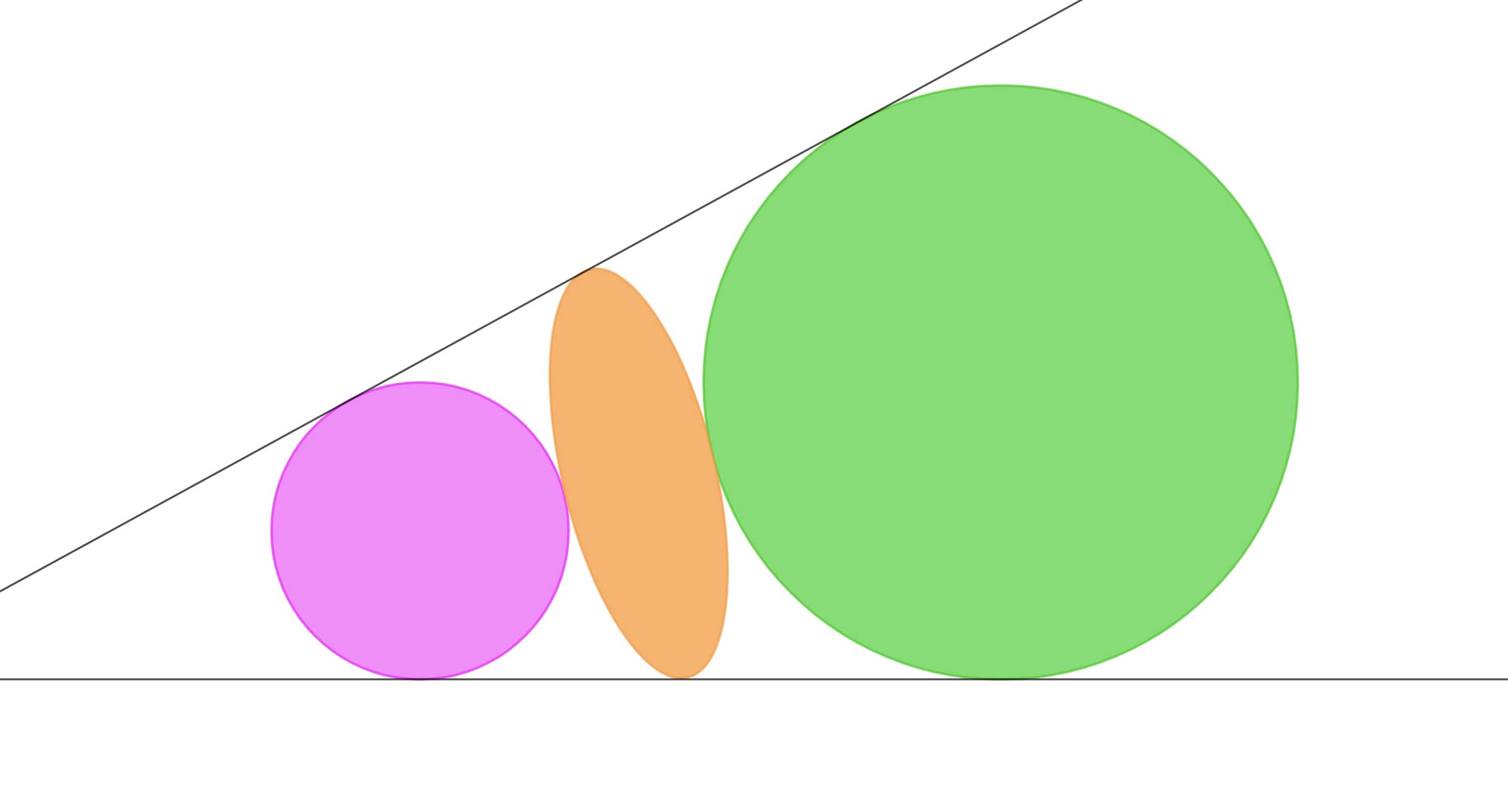
Two circles and an ellipse are tangent to two lines as shown in the figure. The ellipse is tangent to the circles at its minor vertices. If the radii of the circles are 4 and 9, what is the length of the semi-major axis of the ellipse?
The answer is 6.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Actually it makes the question unnecessarily complicate. If we look at the picture, we will realize that the length of Simi-minor axis of eclipse is irrelevant. we can set it as 0, it makes calculation much easier.
Log in to reply
I don't see how the picture tells us that the semi-minor axis is irrelevant, but even if it does, I wouldn't consider this approach as a proof for the final conclusion.
Log in to reply
What is the length of the semi-minor axis of the ellipse? Is it 1.6 ?
Log in to reply
@Vijay Simha – It can be any positive value less than 6.
I couldn't tell the minor axis was irrelevant by looking at the picture. I was only able to discover that fact by solving the problem first. This surprise is what makes the problem interesting to me and is why I posted it.
Rotate the diagram so that the angle bisector is on the y -axis and so that the origin is the center of the ellipse:
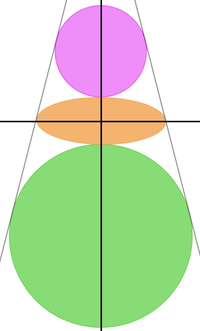
Let the semi-major axis of the ellipse be a and the semi-minor axis be b . Then the equation of the ellipse is a 2 x 2 + b 2 y 2 = 1 , the equation of the top circle is x 2 + ( y − b − 4 ) 2 = 1 6 , and the equation of the bottom circle is x 2 + ( y + b + 9 ) 2 = 8 1 .
Let the equation of the tangent line be y = m x + c . Then the top circle will only have one x -value for x 2 + ( m x + c − b − 4 ) 2 = 1 6 , which means that its discriminant will be zero, or ( c − b ) 2 − 8 ( c − b ) − 1 6 m 2 = 0 , and this solves to c − b = 4 ( m 2 + 1 + 1 ) .
Similarly, the bottom circle will only have one x -value for x 2 + ( m x + c + b + 9 ) 2 = 8 1 , which means that its discriminant will be zero, or ( c + b ) 2 − 1 8 ( c + b ) − 8 1 m 2 = 0 , and this solves to c + b = 9 ( m 2 + 1 − 1 ) .
Similarly, the ellipse will only have one x -value for a 2 x 2 + b 2 ( m x + c ) 2 = 1 , which means that its discriminant will be zero, or a 2 m 2 + b 2 − c 2 = 0 , and this solves to a 2 = m 2 ( c − b ) ( c + b ) .
Substituting c − b = 4 ( m 2 + 1 + 1 ) and c + b = 9 ( m 2 + 1 − 1 ) into a 2 = m 2 ( c − b ) ( c + b ) gives a 2 = m 2 4 ( m 2 + 1 + 1 ) ⋅ 9 ( m 2 + 1 − 1 ) = 3 6 , which solves to a = 6 .
Therefore, the semi-major axis of the ellipse is a = 6 .
Nice job. Notice also that the semi-major axis is always the geometric mean of the radii of the two circles.
Log in to reply
Thanks! I liked Thanos's solution, too. Ours are similar but with a few minor differences.
The whole figure is symmetric about the bisector of the angle formed by the two lines, so we can position it on a coordinate system with the center of the ellipse being the origin, the major axis of the ellipse on the x-axis and the centers of the circles on the y-axis, as shown in the diagram.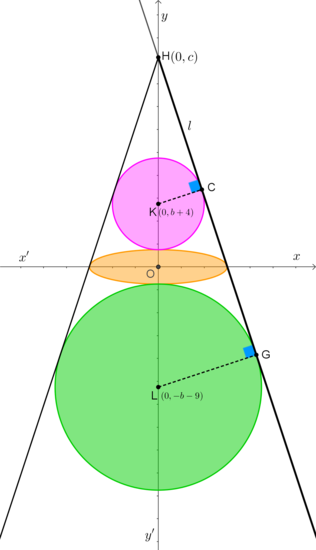 Let the equation of the ellipse be
a
2
x
2
+
b
2
y
2
=
1
, where
a
and
b
are its major and minor semi-axis respectively.
Let the equation of the ellipse be
a
2
x
2
+
b
2
y
2
=
1
, where
a
and
b
are its major and minor semi-axis respectively.
The centers of the small and the big circles are K ( 0 , b + 4 ) and L ( 0 , − b − 9 ) respectively.
The equation of the line l that intersects the positive coordinate semi-axes O x and O y is of the form y = m x + c ⇔ m x − y + c = 0 where the y-intercept c is greater than the y-coordinate of K , i.e. c > b + 4 > 0 .
Since l is tangent to the circles, the distances from their centers to the line equal their radii. Using the formula for the Distance between Point and a Line we have
d ( K , l ) = m 2 + 1 ∣ − b − 4 + c ∣ = 4 ⇔ − b − 4 + c = 4 m 2 + 1 ⇔ c − b = 4 m 2 + 1 + 4 ( 1 )
d ( L , l ) = m 2 + 1 ∣ b + 9 + c ∣ = 9 ⇔ c + b = 9 m 2 + 1 − 9 ( 2 )
Line l is also tangent to the ellipse, i.e. the line and the ellipse have exactly one common point. This means that the system of their equations has exactly one solution. Combining the two equations we get
a 2 x 2 + b 2 ( m x + c ) 2 = 1 ⇔ ( a 2 m 2 + b 2 ) x 2 + ( 2 m c a 2 ) x + ( a 2 c 2 − a 2 b 2 ) = 0 The latter is a quadratic equation and, since it has a unique solution, the discriminant is 0, i.e.
( 2 m c a 2 ) 2 − 4 ( a 2 m 2 + b 2 ) ( a 2 c 2 − a 2 b 2 ) = 0 Rearranging,
a 2 m 2 = c 2 − b 2 ⇒ a 2 m 2 = ( c − b ) ( c + b ) ⇒ ( 1 ) , ( 2 ) a 2 m 2 = ( 4 m 2 + 1 + 4 ) ( 9 m 2 + 1 − 9 ) ⇒ a 2 m 2 = 3 6 m 2 ⇒ m = 0 a = 6