Acceleration on an Elliptical Path
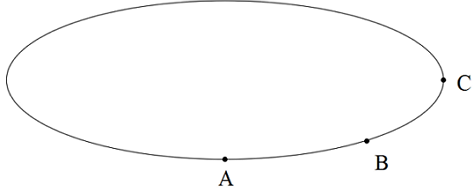
A particle is moving on an elliptical path as shown, at a constant speed. At which point is the particle's acceleration at maximum?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
please...let me know where i am wrong.....i used the parametric equation of ellipse:x=acos(t),y=bSin(t).. and differentiated it twice to get acceleration and it came out to be constant....u could try for yourself..any suggestions?
Log in to reply
Archit ur finding tangential acc. which is const.(actually zero) but u need to find normal acc.....
Well I got the answer as a b c o s e c 2 t... d t d x = -asin(t) and d t d y = bcos(t). Now using the chain rule: d x d y = d t d x d t d y = - a b . s i n ( t ) c o s ( t ) . Now we need to be more careful when working out the 2nd derivative (also I'm going to ignore the constant for now): " d x 2 d 2 y " = d x d [ d x d y ] = d t d [ s i n ( t ) c o s ( t ) ] d x d t (by the chain rule). Now using the quotient rule: d x 2 d 2 y = v 1 d x d u - v 2 u d x d v = -[ s i n 2 t s i n 2 t + c o s 2 t ] = - c o s e c 2 (t). Now multiplying by the constant that we neglected earlier gives: d x 2 d 2 y = a b c o s e c 2 (t)
If there is acceleration, then how can speed be constant?
Log in to reply
It is not tangential acceleration it is radial.It is requires to keep body on given curve.Example when u sit on merry-go-round u experience an outward force so to balance that an inward force is required(equal in magnitude to outward force).Hence this force is not increasig speed.
and BTW pankaj from where are you?
Log in to reply
I am from Jaipur and sorry for replying late..
Log in to reply
pankaj, shouldnt the answer be C tho? since smallest radius
Log in to reply
@Justin Chan – Thanks. We have updated the answer to C.
In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the menu. This will notify the problem creator / staff who can fix the issues.
answer pankaj Are you from North Delhi.
I thought that eclipse shape is just a point of view. But, actually its an eclipse. Poor me
They should have said radial acceleration. Otherwise I understand tangential acceleration
acceleration = t i m e Δ v e l o c i t y and velocity is a vector quantity (it has direction and magnitude), so as the speed (i.e.magnitude) is constant, then the Δ velocity relies on direction. C shows the sharpest turn, so that is where acceleration is greatest
They should have specified what acceleration they referred to.
to maintain constant speed, at higher distance more acceleration is required , c is at higher distance so it is answer.
But by comparing equation of centripetal force=centrifugal force So the account. To equation a=v^2/r Where r is small a is max.
i used the parametric equation of ellipse:x=acos(t),y=bSin(t)....that gives costant acceleration..any suggestions?
i did not undrstnd
In general, there are two types of acceleration according to how they affect speed. If the acceleration is perpendicular to the velocity it affects the direction but never the magnitude (speed) and if it is parallel (or tangent) to it, it affects the magnitude but never the direction. Every acceleration that affects both can be thought of as a combination of those.
Tangent acceleration is defined as the rate of change of the magnitude of the velocity, while the centripetal (perpendicular) acceleration turns out to be equal to the velocity squared times the curvature or the velocity squared over the radius of curvature.
The answer is C, because the radius of curvature is smaller there
BECAUSE RADIUS AT C IS MINIMUM
why did i get b as the answer then?
Log in to reply
Thanks. We have updated the answer to C.
In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the menu. This will notify the problem creator / staff who can fix the issues.
The Radius of curvature at c is smallest.
So acceleration is R v 2 .
Thus, the acceleration is maximized at C .
And radius of curvature can be checked by drawing circles at A , B and C by taking small arcs around them you will get the radius of the circle drawn at is minimum.