Elven Old Traditional Roof Problem?
To solve this problem, I would have to define what "Elven Old Traditional Roof" ( "EOTR" for short) is. Firstly, I will say that it is not the same as "Elven Traditional Roof" ( "ETR" ). That information is rather invaluable.
EOTR is 3D figure, whose base is a rectangle (usually called A B C D where ∣ A B ∣ > ∣ B C ∣ ). It is very similar to the pyramid, but unlike such, it doesn't have a peak point, but it has a peak line P Q . Both points P , Q are on distance H from the base's plane and on the same side of the plane, and the following must be fulfilled to be labelled as EOTR :
- ∣ A P ∣ = ∣ D P ∣ = ∣ B Q ∣ = ∣ C Q ∣ (the length of these segments will be labelled as S ) where P = Q .
- ∣ P Q ∣ = ∣ A B ∣ − ∣ B C ∣
The most important property for every EOTR is volume (obviously). So if we know the following:
- ∣ P Q ∣ = 5 3
- B C A B = 3 . 5
- S = 5 6
Calculate the most important property of the given "Elven Old Traditional Roof" .
Here is one picture that may be helpful in realizing what EOTR is ( enlarge here ):
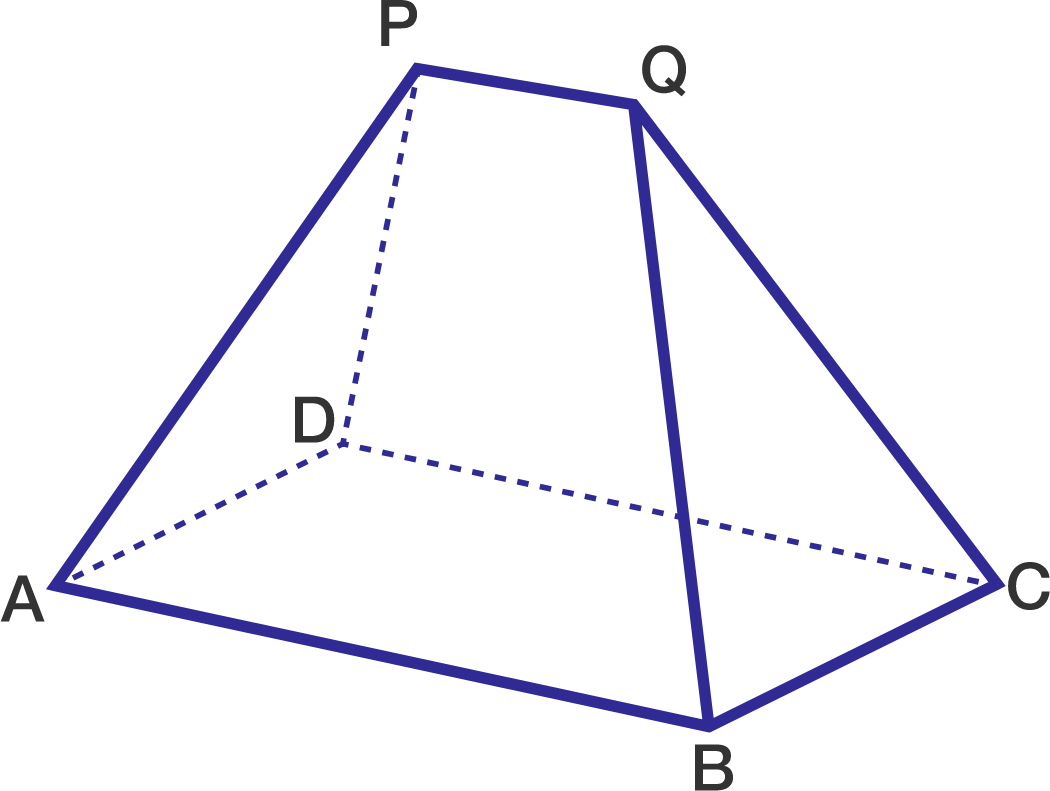 Elven Old Traditional Roof, not the one from the problem though
Elven Old Traditional Roof, not the one from the problem though
If You have any question related to Elven 3D objects, such as this one, or about the problem, feel free to ask it here .
The answer is 228.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
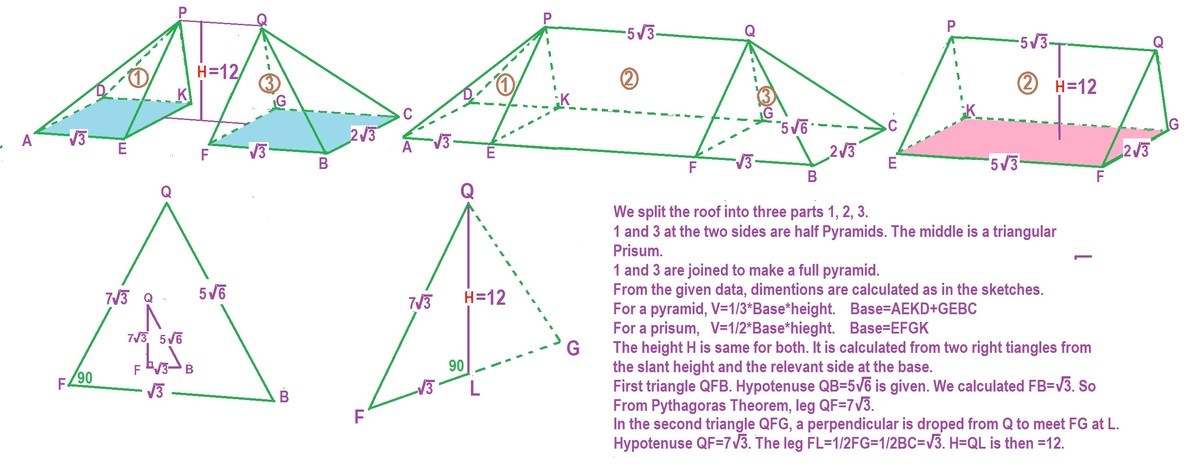 From the given data we get the following values as shown. The sketch shows naming of various point .
From the given data we get the following values as shown. The sketch shows naming of various point .
B
C
A
B
=
3
.
5
,
s
o
A
B
=
3
.
5
∗
B
C
.
B
u
t
P
Q
=
A
B
−
B
C
=
3
.
5
∗
B
C
−
B
C
=
2
.
5
∗
B
C
=
5
∗
3
.
.
g
i
v
e
n
.
∴
B
C
=
2
∗
3
,
A
B
=
3
.
5
∗
B
C
=
3
.
5
∗
2
∗
3
=
7
∗
3
.
B
u
t
P
Q
=
5
∗
3
,
⟹
A
E
+
F
B
=
2
∗
3
.
S
o
A
E
=
F
B
=
3
.
All these dimensions are shown in the sketches. H also is calculated on the sketches. So :-
T
o
t
a
l
v
o
l
u
m
e
=
1
+
3
+
2
=
3
1
∗
2
∗
(
3
∗
2
3
)
∗
1
2
+
2
1
∗
(
5
∗
3
∗
2
3
)
∗
1
2
.
T
o
t
a
l
v
o
l
u
m
e
=
2
2
8
Solution:
Let's introduce new labels: A B = b , B C = a and m = b − a .
So we need to find volume of pyramid whose base is a square with side a + volume of prism of height m and base as isosceles triangle whose unique side is a . ( Enlarge image bellow )
Imagine that we pull out the middle piece and bring leftmost and rightmost pieces together. That is the earlier mentioned "hidden" pyramid. The middle piece is the prism
Firstly we solve the following equation: b − a = 5 3 ; a b = 3 . 5 So the ( a , b ) = ( 2 3 , 7 3 ).
The orthogonal projection of point P is P ′ and ∣ P P ′ ∣ = H . P ′ is equally distanced from A B and B C , so the ∣ A P ′ ∣ = 6 . From here, ∣ P P ′ ∣ is calculated using Pythagoras' theorem, and it is 1 2 . Volume of the pyramid is then 3 1 a 2 H = 4 8 . [1]
For the volume of the prism we need area of base, which is 2 1 a H multiplied by height of the prism, which is in this case b − a . Then the volume is 1 8 0 . [2]
Using [1] and [2], we get that the volume of this 3D object is 2 2 8
What is an "Elven 3D object"?
Log in to reply
That is a very creative name for random 3D object. Maybe one day it will have some real meaning, but not for now.
Log in to reply
Oh, I thought you were a LOTR or D&D fan :)
Log in to reply
@Calvin Lin – Well, when I think about it, I really do not have an argument why I called it an "elven" object. Probably it is mentioned in LOTR and D&D games, but I took it from Elder Scrolls games, where there are some Elven Armors and other stuff, like weapons. But surely, in those games I have not seen/heard for Elven Roof (and especially for Old Traditional one). So some references, imagination and geometry, and here it is, a problem such as this one. :)
Also, could you tell me how a level for a problem is assessed, if not a problem? I assessed this to be level 3 problem, but now it is level 5...
Log in to reply
@Milan Milanic – Less people get your question right ==> The level of your question goes higher.
I approached it with an integral and got 228. I guess that works too.
Let us think about the rectangles that we obtain when we look at a cross section of the EOTR at a height h . We will find a general formula for its sides and integrate over the height of the EOTR in order to find the total volume. Wlog, let us call the side a and b , where a ≥ b and the total height of the EOTR will be called H .
Lemma: The difference between the sides of the cross-sectional rectangles remains constant as h goes from 0 to H .
Proof of the lemma:
In the case of the shortest side, b , we can see that a half-pyramid is formed if we cut vertically through points P and Q , so we can say that the length of the short side changes as h becomes bigger by a factor ( 1 − H h ) . In the case of the longer side, a , it is possible to extend the lines A P and B Q , for example, until they meet at a point at height K , and we can do the same analysis to say that the length of the long side changes by a factor ( 1 − K h ) . Now, at height H , we now that the short side becomes zero and the long side becomes a − b . Therefore:
a ( 1 − K H ) = a − b ⇒ a = b ( H K )
Now, for any height h , we would have:
a ( 1 − K h ) − b ( 1 − H h ) = a − b ( H K ) ( K h ) − b ( 1 − H h ) = a − b
as we wanted to show.
Now that we proved our lemma, we can write the are of the cross-sectional rectangles as:
A ( h ) = s h o r t s i d e ∗ ( a − b + s h o r t s i d e ) = b ( 1 − H h ) ( ( a − b ) + b ( 1 − H h ) A ( h ) = a b − ( b 2 + a b ) ( H h ) + b 2 ( H 2 h 2
The volume would be:
∫ 0 H A ( h ) d x = a b H − ( b 2 + a b ) ( 2 H ) + b 2 ( 3 H )
a and b are calculated using the values of P Q and B C A B . Then, H can be easily calculated using the value of S and doing some Pythagoras.
Inputting these values in the previous expression we get that the volume is 2 2 8 .