Embracing tetrahedra
Geometry
Level
4
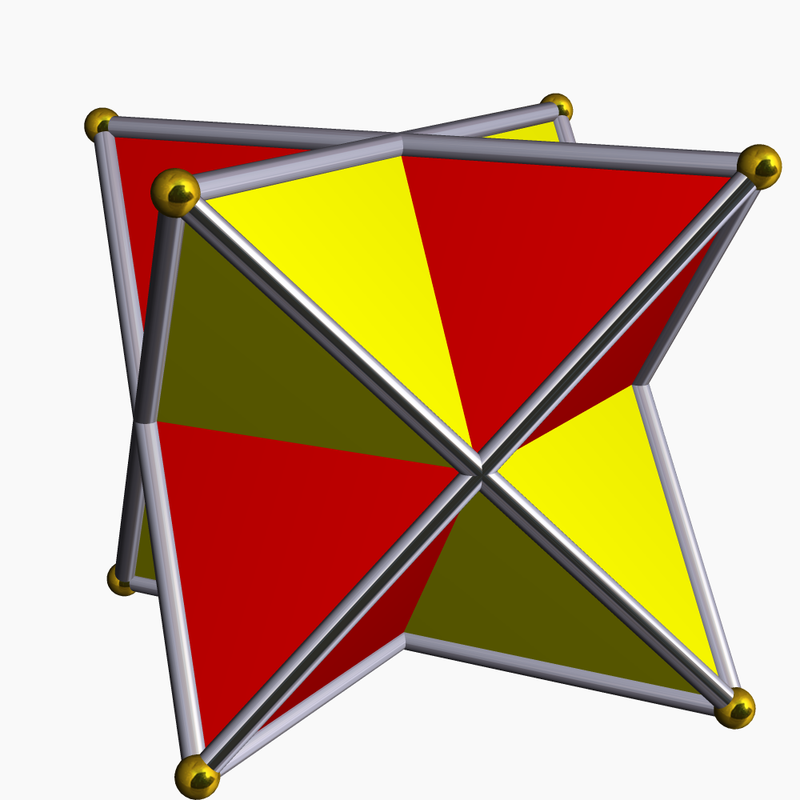
Consider a regular tetrahedron with a volume of 60. Reflect this tetrahedron about its center to obtain a second tetrahedron. Find the volume of the union of these two tetrahedra.
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The union of the two tetrahedra is the disjoint union of one of them (the big red one in the attached figure, say) with four smaller regular tetrahedra (colored yellow in the figure). The small yellow tetrahedra have half the height (and therefore an eighth of the volume) of the big red tetrahedron. Thus the volume of the union is 6 0 + ( 4 ∗ 8 1 ∗ 6 0 ) = 9 0 .