Enlarging Regular Polygons
It is possible to arrange four copies of an equilateral triangle to cover an equilateral triangle with twice its side length. The same holds for a square:
However, doing the same exercise with a regular polygon with more sides requires some overlapping:
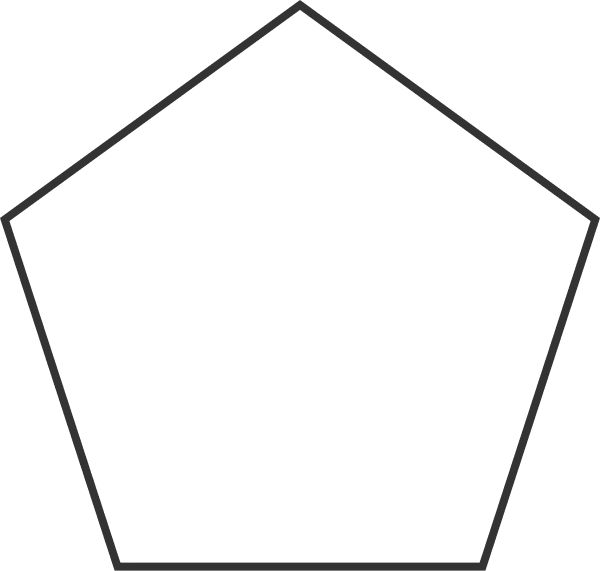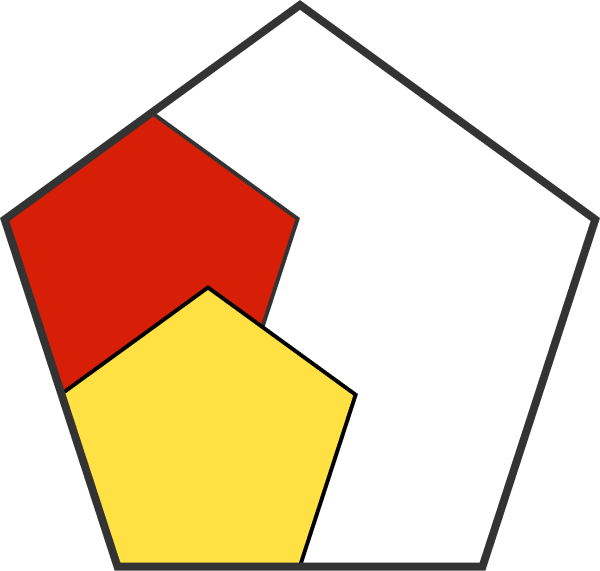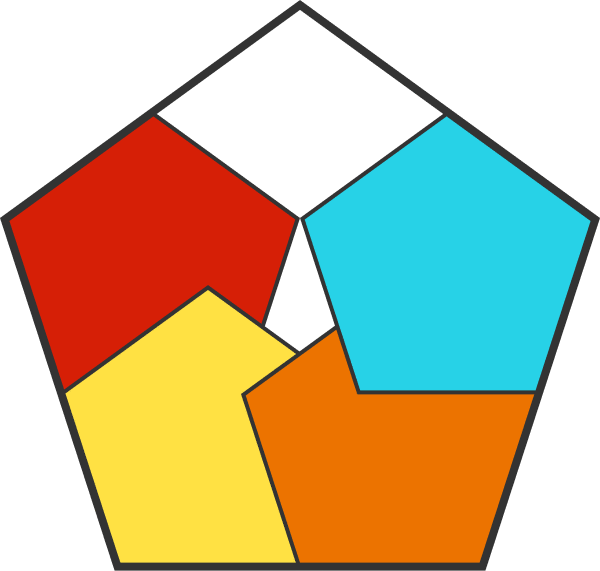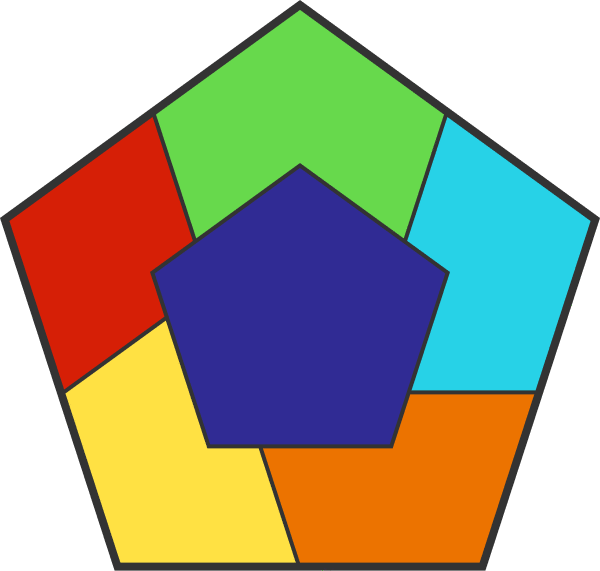 Covering a regular pentagon with double the side length requires 6 pentagons
Covering a regular pentagon with double the side length requires 6 pentagons
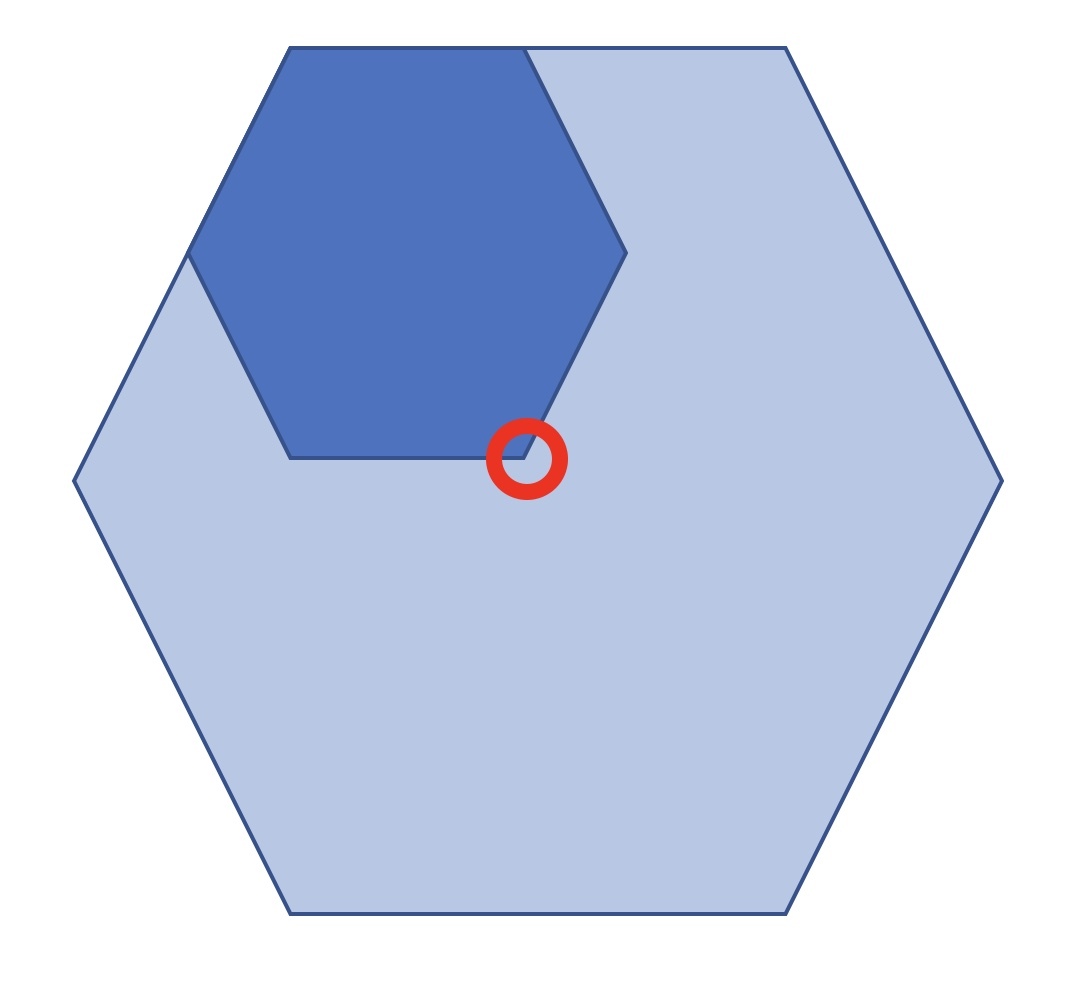
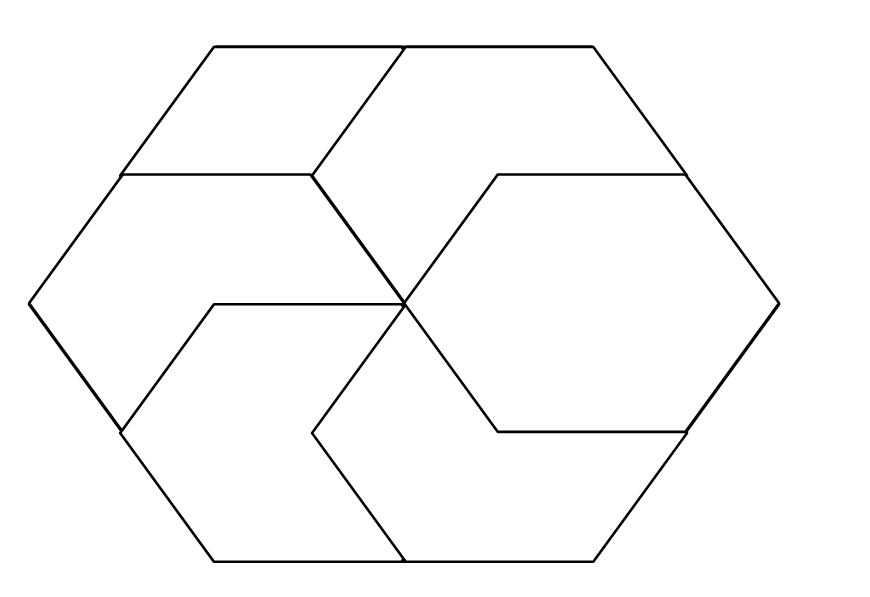
How many identical regular hexagons are needed to cover a regular hexagon with double the side length?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
The most famous instance of this type of problem is a carnival game called "Cover the Red Spot", which involves dropping five smaller circles onto a larger red circle so that all the red is covered.

As the spot is very difficult to cover, most people who play lose, even though the game is not technically "rigged".
Why the solution can't be six small hexagons to completely cover the larger one?
Log in to reply
It is! I only drew one of the six, but yes, you need six of those hexagons to cover the larger one.
I only showed that by covering each vertex, the center of the hexagon is also covered (barely), so that six is sufficient.
Log in to reply
@Arjen Vreugdenhil I understood your example (thank you for adding it here), but in my computer it says 6 is incorrect, even though you've proven to be correct. :(
The largest circle that can be covered by 5 unit circles has a radius about 1.641. Let's say that a carnival operator uses a slightly smaller red circle, so that the placement of the centers off each of the unit circles has a leeway of about 0.1. This allows the carnival operator to quickly show the audience how it can be covered (after practice!), and then whisked away. If the players can only recall roughly the centers with an accuracy of 0.2, then the probability of the correct placement of the first circle would be (0.1/0.2), and thereafter (0.1/0.2)^2, for a total probability of (1/2)^9, or about 1 in 512. So, it is a fair game, and some will win legitimately, and most will lose because looks a lot easier than it really is. An important rule of the game is that once a circle is laid down, it cannot be moved.
Log in to reply
(""The largest circle that can be covered by 5 unit circles has a radius about 1.641"") - will you give me the proof for that?
Log in to reply
This number 1.641 was first determined by computer in 1962, and then later proven by Karoly Bezdek in 1983. You can check out the arrangement for 5 discs in Disc Covering Problem , where it gives r ( 5 ) = 0 . 6 0 9 3 8 2 8 6 4 . . . which is the reciprocal of 1 . 6 4 1 . . . . I've not been able to obtain a copy of Bezdek's 1983 proof.
I have done that same mistake again. I thought that "Double the Sides" meant that the sides on the left and right had to be doubled in order to fit TWO more hexagons. I think I got confused a little bit while reading the question. I would rate this problem a 3 because it is actually quite obvious.
I thought this was a trick question but the answer lies on the caption right below the 6 Hexagons..
Ellegantly clear clean and simple
Yeah it's beautiful
Break the small hexagon into 6 equilateral triangles and the larger one into a lattice with 24 of those triangles. This helps to organize your placement of the hexagons, and then simple trial and error should lead to a configuration in which six is possible. A more interesting question might be to show that this is the minimum. To do this, pick any three sides of the large hexagon that don't touch. Each of these should have exactly two triangles on it; color these in. Notice now that a small hexagon cannot cover two of these colored triangles. Thus, we will need at least six hexagon.
I don't think your argument quite works out. If we allow the small hexagons to lie partially outside the large one (and I think we should!), then one hexagon can indeed cover two of the triangles.
Instead, we can consider the six corners of the large hexagon. We must have all the corners completely covered, in the sense that some small neighbourhood around the corner is covered. Since the distance between two neighbouring corners is the same as the diameter of the small hexagon, each hexagon can either cover exactly one corner completely, or it can barely touch two corners but cover none completely, (or it can touch one or zero corners). A corner needs to (at least) be covered by one hexagon or touched by two, so we might count touching a corner as covering 1/2 corner. In this sense each hexagon covers at most 1 or 1/2 + 1/2 = 1 corner, so we need at least six hexagons.
This is how I confirmed what I was thinking of.
Plz tell me if i am wrong i saw a series that to cover an even side polygon (lets say n sided) you need n number of polygons
And to cover odd sided polygon (lets say x sided) you need x+1 number of polygons
7 regular n-gons are the maximum required to cover one with doubled sides. The can be beaten for n=3 and n=4 (4 copies) n=5 and n=6 (6 copies). Circles require 7.
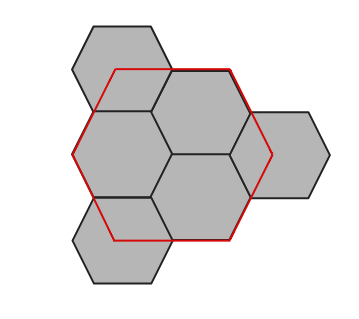
Place six smaller hexagons inside the larger hexagon, with one vertex matching. Then the opposite vertex lies precisely in the center of the large hexagon. Repeating this six times will therefore precisely cover the entire hexagon.