Equal Area and Perimeter
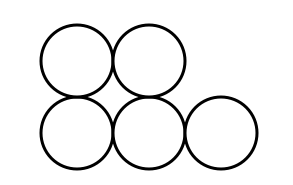
Does there exist a line which divides these 5 circles into two parts of equal area and perimeter?
If no, why not?
If yes, can you find that line?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
That's it.
Ah, very nice. I added another approach. Glad to see that there are many different ways to do this.
I wonder if this is always possible. I think that it is if the figure is convex (which this is not).
Log in to reply
Check out Ham Sandwich Theorem . The answer is, yes, it's always possible, convex or not.
Later, I'll try to find all the other possible ways to cut these circles in half.
Log in to reply
Can you explain how it relates? I think it says "Given 2 figures in 2-D space, there is a line that cuts both of them into equal area (but no restraint on the perimeter)".
However, in this case, the question is "Given 1 figure in 2-D space, there is a line that cuts it into equal area and perimeter".
I think that a way to use the Ham-Sandwich Theorem, is to make thicken the perimeter and consider it as the second figure. That makes me believe it's going to be possible, but I don't know how to finish the limiting argument.
Log in to reply
@Chung Kevin – The Ham-Sandwich Theorem and its variations include perimeters with a measure of length instead of areas. For example, we could have two closed curves, and there would exist a line that divides the perimeter both in half. A related subject is Brouwer Fixed Point Theorem There is a kind of a common thread though all of them, all share the same underlying reasoning.
As an example of Brouwer Fixed Point Theorem, suppose you have two dollar bills that look exactly the same. You crumple one of them up and lay it on the other one that is still flat. There exists at least one point in the flat dollar bill that is immediately below the same point in the other bill which is all crumpled up.
As a still another example, at any given moment, there exist at least two points on Earth opposite of each other (antipodal points) that have the exact same temperature.
YES!I got it too! It wasn't nearly as exact as your but the first example is the way I would have cut it.
Here's another solution:

Log in to reply
That's nice. You take the "center" of the top 2 circles, and connect it to the center of the bottom 3 circles.
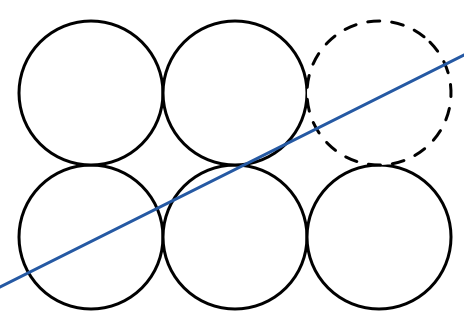
Fill in the missing circle, shown in dotted line.
Take the diagonal line that connects the center of the upper right (dotted) circle, and the center of the 6 circles (tangent point of the 2 middle circles).
This line would perfectly split the area and the perimeter of all 6 circles, and also of the 1 dotted circle.
Thus, this line would perfectly split the area and the perimeter of the 5 remaining circles.
ah, no, it would not split the area and perimeter of the remaining 5 circles, if that corner circle is removed. If the other 5 circles have their areas and perimeters split in half, then necessarily the 6th one would have its own area and perimeter split in half, and that's generally not the case.
Edit: If you adjust that blue line just a bit, then you'd be correct. See my explanation of how this can be done. That blue line needs to pass through the center of that dotted circle.
Log in to reply
Yes, that's what I described, but I drew the image wrongly. I've fixed it now.
Log in to reply
Now that's cleared up, I've attributed this solution to you, see my posted answer.
If you take the radius of the circle to be 1 unit, and the origin as the center of the downleft circle, the center of mass (for both area and perimeter) would be 5 4 ( 1 , 1 ) + ( 4 , 0 ) = ( 8 / 5 , 4 / 5 ) , and every line going to that point is a valid answer.
Let point P be at the center of the first four circles in the square cluster, and point Q be at the center of the 5th circle. Then the line P Q passing through both will divide both the total area and total perimeter by exactly half.
To understand why, first note that the line PQ runs through the center of the 5th circle, dividing that circle's perimeter and area in half. Now, for symmetry reasons, because line PQ runs through the point that is at the center of the square cluster of circles, however it divides the circles on one side, it divides the circles on the other side equally, thus dividing the total area and total perimeter of those four circles in half. Hence, the total area and total perimeter of all five circles are both divided in half.
Here's another way [per Chung Kevin] to split the five circles. First, add a sixth circle (green). Let point P be at the center of the six circles, and point Q be at the center of the 6th (green) circle. Then the line P Q passing through both will divide both the total area and total perimeter by exactly half not only of all six circles, but of the five black circles as well.
The reasoning is the same as above, with the difference is that since the sixth circle (green) is split in half, area and perimeter, then we can subtract this circle from the cluster of six circles, leaving the line splitting the remaining five circles in half as well, area and perimeter.