Equal perimeter and area

• For small triangles, the perimeter will be a larger number than the area.
• To maximize the area, make the triangle equilateral.
• You can increase the perimeter of a triangle without changing its area by skewing it.

So let's begin by considering equilateral triangles where $p=3s$ and $A=\frac{\sqrt{3}}{4}s^{2}$

Since we want the area and perimeter equal we can write $3s=\frac{\sqrt{3}}{4}s^{2}$

Which solves to $s=4\sqrt{3}$ hence $A=p=12\sqrt{3} \approx 20.8$

This is the minimum of any triangle with equal perimeter and area. We need an integer so increase $A$ to $21$ which will make the perimeter slightly less. Then just skew it a bit to make $p=A=\boxed{21}$

---

$\triangle ABC$ is the smallest triangle with equal perimeter and area, it is equilateral.

$\triangle DEF$ is enlarged so its area is an integer, $21$ . But the perimeter is less.

Slide $F$ to $F'$ to increase the perimeter to $21$ while keeping the area fixed.

By Heron's formula, the area of a triangle with side lengths $a,$ $b,$ and $c$ is:

$A = \frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}$

In this problem, the triangle's area is equal to its perimeter, so:

$A = a+b+c = \frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}$

Some more algebraic manipulation:

$\begin{array}{lr} (a+b+c)^2 = \frac{1}{16}(a+b+c)(-a+b+c)(a-b+c)(a+b-c) & \text{Square both sides} \\ a+b+c = \frac{1}{16}(-a+b+c)(a-b+c)(a+b-c) & \text{Divide both sides by } (a+b+c) \\ 16A = (-a+b+c)(a-b+c)(a+b-c) & \text{Multiply both sides by 16 and substitute } A \\ \end{array}$

Now note that the three factors in the right side are all positive due to the Triangle Inequality. It is also possible that they are all equal. We can apply AM-GM:

$\begin{array}{lr} \frac{(-a+b+c)+(a-b+c)+(a+b-c)}{3} \ge \sqrt[3]{(-a+b+c)(a-b+c)(a+b-c)} & \text{AM-GM inequality} \\ \frac{a+b+c}{3} \ge \sqrt[3]{(-a+b+c)(a-b+c)(a+b-c)} & \text{Simplify} \\ \frac{A}{3} \ge \sqrt[3]{16A} & \text{Substitution} \\ A \ge 12\sqrt{3} & \text{Solve for }A \\ \end{array}$

The equality is satisfied when $-a+b+c=a-b+c=a+b-c.$ This gives an equilateral triangle with side lengths $4\sqrt{3}.$ $12\sqrt{3} \approx 20.785,$ so the next largest integer is $\boxed{21}.$ An example of a triangle that has this area/perimeter is $(6.5,7,7.5).$

---

Note : It's tempting to use AM-GM with the four factors in the right side of Heron's formula:

$A = \frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}$

However, it is not possible for the factor $(a+b+c)$ to be equal to the other three factors. In this case, the AM-GM inequality will give a bound on the solution, but it will not give the minimum.

From $K = rs=\frac{rp}{2}$ we get that the inradius of the triangle is 2. Now, it is intuitively obvious that for fixed inradius, the area is minimized when the triangle is equilateral, so we have an equilateral triangle of side length $4\sqrt{3}$ and we can quickly finish and get an answer of $\lceil 12\sqrt{3} \rceil = \boxed{21}$ . It is simple to show that this is obtainable.

For completeness, let us prove that the equilateral triangle is indeed the minimal case. We operate on the following marked angles:

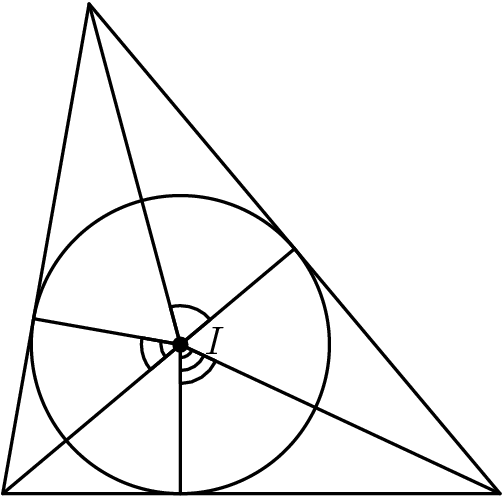
Let these be $\theta_1$ , $\theta_2$ , and $\theta_3$ . We have that $\theta_1+\theta_2+\theta_3=180^\circ$ , and the area of the triangle is: $r(r\tan(\theta_1))+r(r\tan(\theta_2))+r(r\tan(\theta_3))=r^2(\tan(\theta_1)+\tan(\theta_2)+\tan(\theta_3))$ It suffices to minimize $\tan(\theta_1)+\tan(\theta_2)+\tan(\theta_3)$ . Note that $0 \leq \theta_1,\ \theta_1,\ \theta_1 \leq \frac{\pi}{2}$ , and on this interval, $\tan(\theta)$ is convex. Hence, by Jensen's Inequality: $\frac{\tan(\theta_1)+\tan(\theta_2)+\tan(\theta_3)}{3} \geq \tan\left(\frac{\theta_1+\theta_2+\theta_3}{3}\right) = \tan(60^\circ) = \sqrt{3}$ So $\tan(\theta_1)+\tan(\theta_2)+\tan(\theta_3)$ is minimized at $3\sqrt{3}$ . Equality holds only when either our function is linear (tangent clearly isn't linear) or the function arguments are all equal, hence $\theta_1=\theta_2=\theta_3=60^\circ$ . This implies that the triangle is equilateral when the area is minimal.

If the triangle has sides $a,b,c$ and semiperimeter $s$ , write $u = s-a$ , $v = s-b$ , $w = s-c$ . Then $u+v+w=s$ and so the triangle has perimeter $2(u+v+w)$ and area $\Delta = \sqrt{(u+v+w)uvw}$ . Thus we require that $4(u+v+w) = uvw$ , and hence that $uv > 4$ and that $w \; = \; \frac{4(u+v)}{uv-4}$ in which case the triangle has area $\Delta = \frac{2uv(u+v)}{uv-4}$ . Thus $u+v = \frac{(uv-4)\Delta}{2uv}$ and hence $u,v$ are real roots of the quadratic $X^2 - \frac{(uv-4)\Delta}{2uv}X + uv \; = \; 0$ so this quadratic must have nonnegative discriminant, so that $\begin{aligned} \frac{(uv-4)^2\Delta^2}{4u^2v^2} - 4uv & \ge \; 0 \\ \Delta^2 & \ge \; \frac{16u^3v^3}{(uv-4)^2} \\ \Delta & \ge \; \frac{4(uv)^{\frac32}}{uv-4} \end{aligned}$ It is easy to see that the function $g(t) = \frac{4t^{\frac32}}{t-4}$ (for $t > 4$ ) has minimum $12\sqrt{3}$ when $t=12$ , and so certainly $\Delta \ge 12\sqrt{3}$ .

The smallest integer value of $\Delta$ that satisfies this condition is $\boxed{21}$ . For this value of $\Delta$ we can obtain $u=\tfrac72$ , $v=3$ , $w=4$ , so that $a = v+w=7$ , $b=u+w=\tfrac{15}{2}$ , $c = u+v = \tfrac{13}{2}$ .

Wow, I’m reading the posted solutions...I thought we had to find one. Just saying the minimum is 21 without actually finding it seems a bit incomplete. If we put a 5, 12, 13 triangle next to a 9, 12, 15 triangle, we have a triangle of sides 14, 13, 15, P = 42 and A = 84. Scaling this triangle by a factor of P/A = 1/2 gives us 7, 6.5, 7.5 which has A = P = 21.

I had worked on a similar problem in the past where A = P AND the sides, as well as A and P, have to be integers. There are two right triangles that satisfy that: 6, 8, 10 and 5, 12, 13. If we take the equation a + b + sqrt(a^2 + b^2) = ab/2, we can eventually manipulate it to b = 4(a - 2)/(a - 4). It’s not hard to show that a = 6, 8, 5, or 12 are the only values that make b, A and P integers.

There are three other triangles with all sides integers and A = P. These are formed by cutting a smaller right triangle out of a larger right triangle. It’s a little tougher proving these are the only 3, but I finally did that a few years ago (proof left to the reader!). The three obtuse triangles with integral sides and A = P are (9, 10, 17), (7, 15, 20), and (6, 25, 29).

For a fixed perimeter $P$ of a triangle, the minimum area occurs for a nearly "flat" triangle with an area just greater than $0$ , and the maximum area of a triangle occurs for an equilateral triangle with an area of $\frac{\sqrt{3}}{4}(\frac{P}{3})^2$ (see here for several proofs of this), so there exists an area $A$ such that $0 < A \leq \frac{\sqrt{3}}{4}(\frac{P}{3})^2$ .

For $P = A$ , we have $0 < P \leq \frac{\sqrt{3}}{4}(\frac{P}{3})^2$ , which solves to $P \geq 12\sqrt{3} \approx 20.7846$ , and the smallest integer value such that $P > 20.7846$ is $P = A = \boxed{21}$ . (One example is a triangle with sides $6.5$ , $7$ , and $7.5$ .)

Assuming isosceles triangle with base '2y' and height 'x' ,

xy=area,

2y+2√(x^2+y^2)=perimeter.

Solving for area = perimeter = integer = 21, using WolframAlpha, script

"solve xy=21, 2y+2√(x^2+y^2)=21"

a solution exists for two triangles as below:

(1) x=5.55373, y=3.78124,

(2) x=6.55678, y=3.20279,

Answer=21.