Equal Products
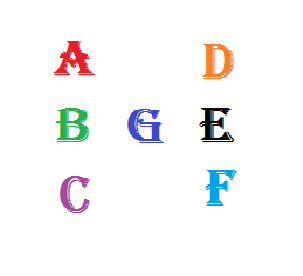 In the figure above, each letter represents a distinct single digit among
0
,
1
,
2
,
…
,
9
.
They are positioned in such a way that
A
×
B
×
C
=
B
×
G
×
E
=
D
×
E
×
F
.
In the figure above, each letter represents a distinct single digit among
0
,
1
,
2
,
…
,
9
.
They are positioned in such a way that
A
×
B
×
C
=
B
×
G
×
E
=
D
×
E
×
F
.
What digit does the letter G represent?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
From your conclusion of G being either 2 or 8, we can eliminate 8 without doing any calculations, because it is not part of the possible solutions.
Log in to reply
But we most to have another foundation to elimine the answer 8. Zakir gave us. :-)
Oh, yes, it's not in choices.
AWESOME PROOF!
Well played *clap
Answer:
If any of these values equals to 0, then A × B × C = B × G × E = D × E × F = 0 .
But since only one of them can be 0, then at least one of A , B , C is equals to 0 and at least one of D , E , F is equals to 0. But this is a contradiction because exactly one of them can be equals to 0 only.
Similarly, iIf any of these values equals to 5, then A × B × C , B × G × E , D × E × F ends with a value of 5 or 0.
But since only one of them must be divisible by 5, then at least one of A , B , C is 5 and at least one of D , E , F is equals to 5. But this is a contradiction because exactly one of them can be equals to 5 only.
Analogously, we can show that none of them can be 7.
We can finish the entire puzzle off quickly after knowing that 0,5,7 can't be the possible values.
Hey everybody, I understand the way you see solutions of this one, But I've just failed this question and the possible answers were 0,2,3,4,9. So te argument 5 and 7 can't be used this time. Please somebody explain how's the solution in my case.
There's nothing that precludes using negative numbers, so there are other solutions. For example 3 is a valid solution for G if A=-3, B=-4, C=1, D=2, E=-1, F=-6.
Log in to reply
Thanks. I've updated the problem statement to reflect this. Those who previously answered 3 has been marked correct.
In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the “line line line” menu in the top right corner. This will notify the problem creator who can fix the issues.
How do you know that?
You should explain why 0, 5 and 7 cannot be any of these numbers and that the middle is forced to be 2 because the product of the remaining numbers is a perfect square.
Log in to reply
well I dont know about 5 or 7 but 0 can't work as any letter because the product of would be 0 for one of the groupings which wouldnt work for them all equalling the same amount; seeing as they have to be distict digits in each letter.
Log in to reply
If 5 or 7 are used in one of the groups, then so as to make product equal, other groups must also have factors of 5 or 7 but it is not possible since the next factor of 5 and 7 are 10 and 14 respectively but they are of two digits
Log in to reply
@Rehman Hasan Tyeb – very nice. thanks for that. i didnt even take more than a second to think that deep into it when responding to Pi. lol great response though :-)
Lets first rule out some numbers 0 7 and 5,
0 makes the entire equation not work as there must be 3 0 terms and we cant have 3 0 terms.
Sue to the size of our set 5 and 7 are also not possible as we would need a factor of 5 to exist in each of the three equation fragments.
other primes like 2 and 3 are okay. a could be 2 b could be 4 d could be 8. a could be 3 b could be 6 e could be 9
g = ac/e =df/b
the numbers, we have available are 1 2 3 4 6 8 9
within this set we have 7 factors of 2 and 4 factors of 3 We need an equal number of factors on each side of the equation. Which leaves us with 5 on one side 5 on the other, meaning g must be 2 or 3. Since we must remove 1 factor only from the equation.
However it cant be 3, as there are only 3 remaining factors of 3, and we require an odd number of factors on each side.
Therefore g must = 2
Can you explain me why you have taken A=6,B=4....why not any other number???
0 is obviously not the answer.I then eliminated 3,9 and 4 using contradiction to get the answer.
You know that 0 can’t be in it because then all the products must equal 0. You know 5 and 7 can’t be in it because their squares are above ten. That leaves you with 1,2,3,4,6,8,9. In order for 8 and 9 to both be included, their LCM.. 72, has to be the least possible product of the three digits: (8,9,1) (9,2,4) (6,4,3)
As other solutions have described, there are a number of ways to prove that none of the digits can be 0, 5, or 7. I found the simplest way to conceptualize this is to be:
- As 7 is prime and has no single-digit multiples, it is impossible for these expressions to be equal unless they all include 7 or none of them include 7.
- The same is true for 5.
- Similarly for 0, it is impossible for these expressions to be equal unless they all include 0 or none of them include 0.
- Since there is no common integer shared by all 3 expressions, we can rule out any of the integers being 0, 5, or 7.
- Therefore, the 7 integers used are 1, 2, 3, 4, 6, 8, and 9.
Then let n = A × B × C = B × G × E = D × E × F
We can infer that n must be factorable by all seven of these integers. The lowest common multiple for these numbers is 72. Conveniently, there are three possible ways to factor 72 into three distinct integers are:
- 9 × 8 × 1
- 9 × 4 × 2
- 6 × 4 × 3
Looking at the initial equation, we can see that B and E are used twice. Since 9 and 4 are the only integers that appear twice in the above list, we can infer that B = 9 or 4, and E equals 9 or 4 (whichever is not B). Thus:
- n = B × G × E
- 7 2 = 9 × G × 4
- 2 = G
Note that this solution does not prove that n must equal 72; only that there is a legal solution in which n = 72 and G = 2.
This was trickier than I thought it was at first glance. I first eliminated the obvious 0 as Dinesh did. And as Dinesh did, I saw that 5 and 7 can't go anywhere because there weren't multiple 5s and 7s to support the other multiplications.
I spent longer than I thought I would on what the product would be. Perhaps I convinced myself it was 48 and couldn't make anything work. When I finally broke out the remaining numbers {1,2,3,4,6,8,9} to the product of primes, it was clear that I needed to 2^3 and 3^2 in all of them.
ABC = BGE => AC = GE BGE = DEF => BG = DF
all are distinct numbers. possible combinations of AC ,GE and BG, DF will be
3 * 2 , 6 * 1 and
4 * 2 , 8 * 1 and
4 * 3 , 6 * 2 and
3 * 6 , 9 * 2 and
4 * 6 , 8 * 3
common integer in the ablove 2 combinations is G,
possible combinations of AC ,GE and BG DF are
3 * 2, 6 * 1 and 4 * 2, 8 * 1 => 2 common numbers (1,2)
3 * 2, 6*1 and 4 * 3, 6 * 2 => 2 common numbers (3,2)
3 * 2, 6 * 1 and 6 * 3, 9 * 2 => 3 common numbers (3,2,6)
3 * 2, 6 * 1 and 4 * 6, 8 * 3 => 3 common numbers (3,2'6)
4 * 2, 8 * 1 and 4 * 3, 6 * 2 => 2 common numbers (4,2)
4 * 2, 8 * 1 and 6 * 3, 9 * 2 => 1 common number (2)
4 * 2, 8 * 1 and 4 * 6, 8 * 3 => 2 common numbers (4,8)
4 * 3, 6 * 2 and 3 * 6, 9 * 2 => 2 common numbers (6,2)
4 * 3, 6 * 2 and 4 * 6, 8 * 3 => 3 common numbers (4,6,3)
Answer must be 4 * 2, 8 * 1 and 6 * 3, 9 * 2 => which have only one common number (2) which is G so the answer is obviously 2.
Correct me if I'm wrong, but it looks like you left out the combination of "3 * 6, 9 * 2 and 4 * 6, 8 * 3 => 2 common numbers(4, 6)" in your proof. Also, "3 * 2, 6 * 1 and 4 * 6, 8 * 3" has only 2 common numbers(3, 6), not 3. Still nice though - I used the brute force 'code breaker' method as well. ;)
A x B x C = B x G x E > A x C = G x E B x G x E = D x E x F > B x G = D x F
I found the answers by trial A=4 B=5 C=3 D=1 E=6 F=10 G=2
4 x 3 = 2 x 6 5 x 2 = 1 x 10
F cannot be 10 because each letter represents a distinct single digit.
we should look out for 7 numbers because thaere are only 7 alphabets. Find the only number which is divisible by seven DISTINCT numbers. By calculation the oddsv we get 72 as that number. 72 has- 1,2,3,4,6,8 and 9 divisible to it. then you rearrange these numbers to get 3 1 4 2 9 6 8
- 1) None of these digits can be 0, because one product will turn to zero while others won't
- 2) Of all digits exclude also 2 highest primes: 5 and 7. Because again if one product contains any of these, then others won't be able to have them.
- 3) We have only 1,2,3,4,6,8,9 left and all these numbers can be represented as products of 2 and 3.
- 4) Consider numbers 3,6,9 as they are the only source of 3s. B=9 D=3 F=6 (or any simmetrical allocation) is the only option which will provide each of the products with exactly 3*3.
- 5) Now it is easy to allocate all the remaining numbers with G=2 being the only option.
You just take A B C and consider them a single digit like 2 and do the same to D E F after that you get this 2x2x2=2xGx2=2x2x2 Is approximately 8=4xG=8 and if we consider G to be 2 then the equation is right but it only works if you use 2 if you use 3 then you will get 3 i know a bummer right?
This may help: https://www.desmos.com/calculator/2jls3fklcs
Here's how I solved the puzzle: The puzzle takes 7 digits, so three must be eliminated. Eliminate digits that don't contain any common factors (besides 1) with other digits since there will be no way to replicate that product in another row or column. That means 0, 5 and 7 are out. Now if you look for digits with common factors, let a = 2 and b = 3. Then 4 = a^2, 6 = a b, 8 = a^3 and 9 = b^2. To solve the puzzle, each row and column needs the least common multiple (LCM) of these numbers which is (a^3) (b^2) = 72.
You can view my solution here: https://www.desmos.com/calculator/mtglzsqk8j
Let's denote A x B x C = B x G x E = D x E x F = P.
It must be possible to "divise" P into at least 5 integers:
P = a * b * c * d * e
in order that these 5 can be "re-grouped" into 3 in at least two mutually exclusive different ways:
P = (a * b) * (c * d) * e = a * (b * c) * (d * e) = A x B x C = D x E x F
otherwise, e.g. if for example it is only possible to have
P = a * b * c * d
then it cannot be the product of two mutually exclusive sets of 3 integers (ABC and DEF).
Therefore, at least two of each of {A, B, C} and {D, E, F} have to be composite (non-prime) integers.
There are only four composite integers available: 4, 6, 8, 9.
If we group this into {4, 6} and {8, 9}, and add to these sets respectively 3 and 1:
3 x 4 x 6 = 1 x 8 x 9 = 72
From the remaining integers: {2, 5, 7}, 72 is divisible only into 2, therefore:
3 x 4 x 6 = 4 x 2 x 9 = 1 x 9 x 8
G = 2
We can show easily that 0, 5 and 7 can't take there.
So we get A × B × C × D × E × F × G = 1 × 2 × 3 × 4 × 6 × 8 × 9 = 1 × 2 × 3 × 2 2 × 2 × 3 × 2 × 2 × 2 × 3 × 3 = 2 7 × 3 4
Since A × B × C = D × E × F
=> ( A × B × C ) 2 × G = ( 2 3 × 3 2 ) 2 × 2 or ( 2 2 × 3 2 ) 2 × 8
So, G = only either 2 or 8.
But we can't take G = 8 as then A × B × C = 36
And we know A × B × C = B × G × E
=> B × E = G A × B × C = 8 3 6 = 4.5 that is not an integer, so not acceptable.
So, G = 2 is the answer.