Equalities
a and b are real numbers, and a ÷ b = a × b = a + b .
What is a − b ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Moderator note:
As the comments point out, the first equation being looked at of a ⋅ b = a / b is equivlent to a ( b − b 1 ) = 0 , from which we get that a = 0 or b = ± 1 . We do need to look at the case when a = 0 .
Given a = 0 , a b = a + b implies b = 0 ; this causes division by zero with b a , so a = 0 .
You didn't notice the case of a = 0 which solves a b = b a
Log in to reply
But then that would imply b = 0 for the third part of the equation, which would make b a undefined.
Log in to reply
Yes, but that case must be considered to confirm that the answer is unique.
Log in to reply
@Jesse Nieminen – Questions faulty
Log in to reply
@Menachem Gavert – No, the question is correct, this answer is slightly incomplete. a=0 must be considered, and scrapped as it implies b=0, making a/b undefined. And a-b is not calculated at the end. But with the given values of a and b, a − b = 2 1 − ( − 1 ) = 2 3 .
https://brilliant.org/problems/prove-this-looks-easy-huh/
where did you get "a-b"?
Log in to reply
I got "b" is -1 and "a" is 1/2, then "a-b" is 3/2, anything wrong?
Log in to reply
I'm still kind of confused how you got "a-b = ab+1-b"
Great solution!!
This was great! I tried something like this but kept solving past a=ab^2 to get a/a=b^2 which then solves down to 1=b which just didn't allow for a value that worked for "a" after that. So I did something wrong, I guess it's that I forgot that -1 was also a valid solution for the square root of 1. Which means I was supposed to get +-1=b and then I could test both values to see which one solves correctly for "a". I'll try not to forget that in the future.
Thanks again for a clear solution!
I'm not clear how you get ab+1=a. Can you help me?
Log in to reply
Since "ab b+b=ab", so on the left, you divided "ab b+b" by "b", and on the right, you divided "ab" by "b", too, then you can get "ab+1=a".
good job!!!
+1 for MS Paint
Log in to reply
I don't know how to type these mathematical operation symbols.
b a = a b ⟹ a ( b 2 − 1 ) = 0 ⟹ b = ± 1 Note that a = 0 since the cases b a = a + b and a b = a + b become false in case a = 0 ⟹ b = 0 (not possible) too .
Now b a − 1 = a + b − 1 ⟹ b a − b = a + b − 1 ⎩ ⎨ ⎧ a = a + 1 0 = 1 c ( absurd ) if b=1 a = − a + 1 a = 2 1 if b =-1 Therefore the required value of a − b = 2 1 + 1 = 2 3
technically 0 is also correct
Log in to reply
No its not, because if a is 0 b is 0 and b can not equal 0 for a real solution.
Great. Love it.
https://brilliant.org/problems/prove-this-looks-easy-huh/
a and b cannot be integers
yeah they can
Log in to reply
Oh really, prove it
Log in to reply
i'm stupid
Log in to reply
@Nishant Sahoo – Its okay but you should have thought about it before posting a comment
Well b can be,but a can't
Log in to reply
yeah I know that
ab = a + b (given) ⇒ a = ab + 1 ⇒ b = 1 - 1/a = 1/-2a Therefore: 1 - 1/a = 1/-2a
Let’s solve for a, 1 = 1/2a ⇒ a = 1/2
Let’s solve for b, b = 1 - 1/a ⇒ b = 1 - 1/(1/2) ⇒ b = -1
Therefore: a - b = 1/2 + 1 = 3/2
-
a*b=a/b solve for b, you get plus minus square root of 1. It can't be 1, because, then a/1=a. But then a+1 does not equal a. So it must be -1. b=-1
-
You plug in -1, and solve for a a(-1)=a=+(-1) -a=a-1 -2a=-1 a=-1/2
-
substitute into original a-b (-1/2)-(-1) 3/2
Done
this is my solution, its longer then the others but maybe someone will find it easier to understand
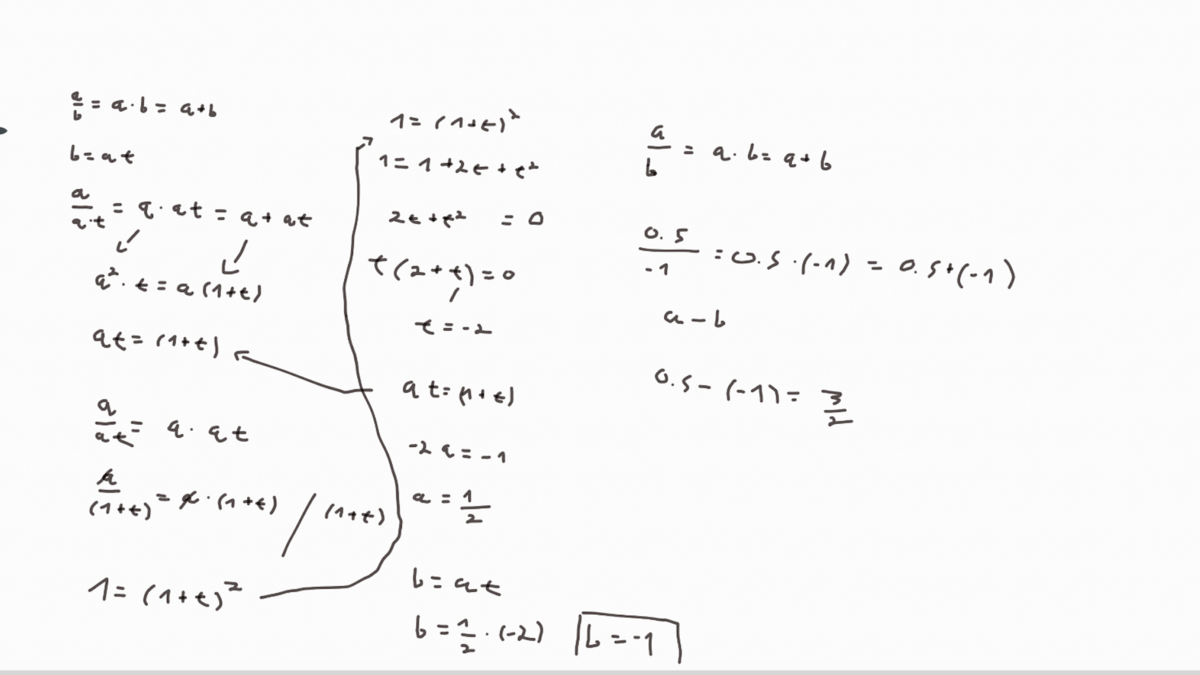
My reasoning went as follows:
If a : b is the same as a ∗ b then b must be either + 1 or − 1 .
When we try a = 1 we end up with: a : 1 = a ∗ 1 = a + 1 , simplified to a = a + 1 which is a contradiction.
So let's try a = − 1 :
a : − 1 = a ∗ − 1 = a − 1 , simplified to − a = a − 1
This is much better. If we now substract a from both sides of the equation we get:
− 2 a = − 1 . Divide both sides by -2 and receive a = 1 / 2
So our result is b = − 1 , a = 1 / 2 and therefore a − b = 1 / 2 − ( − 1 ) = 3 / 2
a/b=ab, b^2=1, b=1,-1, Now. ab=a+b, a+b-ab=0. We have two options either b=1 or b=-1. b=1 then a=0, Won't satisfy (a/b=a*b=a+b) If b=-1 then a=1/2. This satisfying the previous. So a-b =1/2-(-1), =3/2
First from { a b = b a ⟹ a = a b 2 a + b = a b then a b 2 + b = a b ⟹ a b + 1 = a
Next from { ∴ a − b = a b + 1 − b a + b = a b then a − b = a + b + 1 − b ⟹ a − b = a + 1 ⟹ a − b = a − ( − 1 ) ⟹ b = − 1
Finally from { b = − 1 a b = a + b then − a = a − 1 ⟹ a − ( − a ) = 1 ⟹ a + a = 1 ⟹ 2 a = 1 ⟹ a = 2 1
And 2 1 − ( − 1 ) = 2 1 + 1 = 2 1 + 2 2 = 2 1 + 2 = 2 3
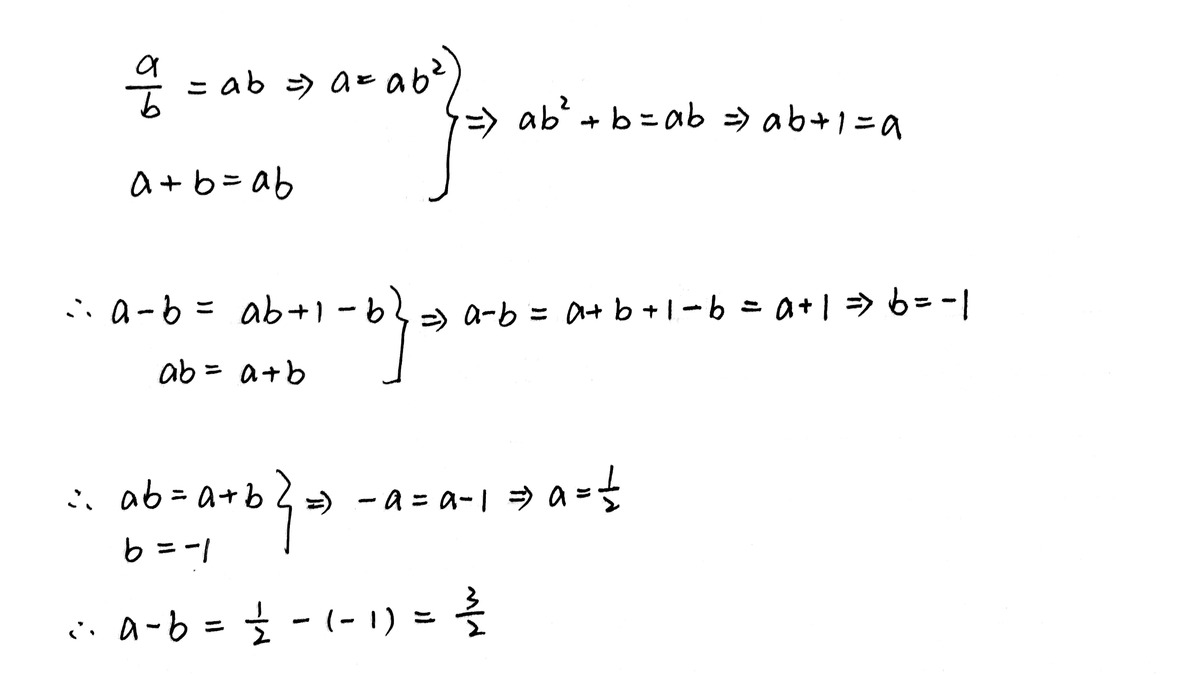
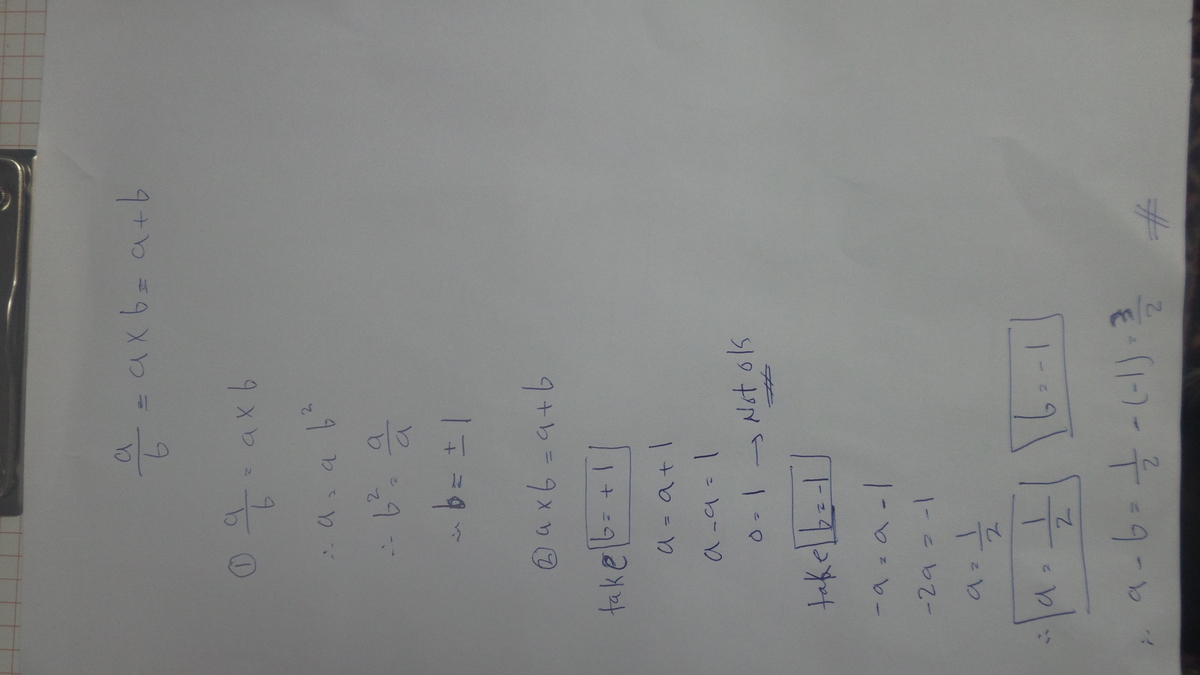
From a ⋅ b = b a is b = ± 1 . But b = 1 ⇒ a = a + 1 . Absurd. Now, if b = − 1 ⇒ − a = a − 1 ⇒ a = 2 1 .