Equation solving
I have a problem with mathematics. It is based on Trigonometry, Geometry and Algebra.
If a circle has a chord 10 unit, and its' minor arc is 16 unit then what is the radius of the circle.
I can't go more than - 5=r.sin(1440/(pi*r)).
Now someone help me to solve for r.
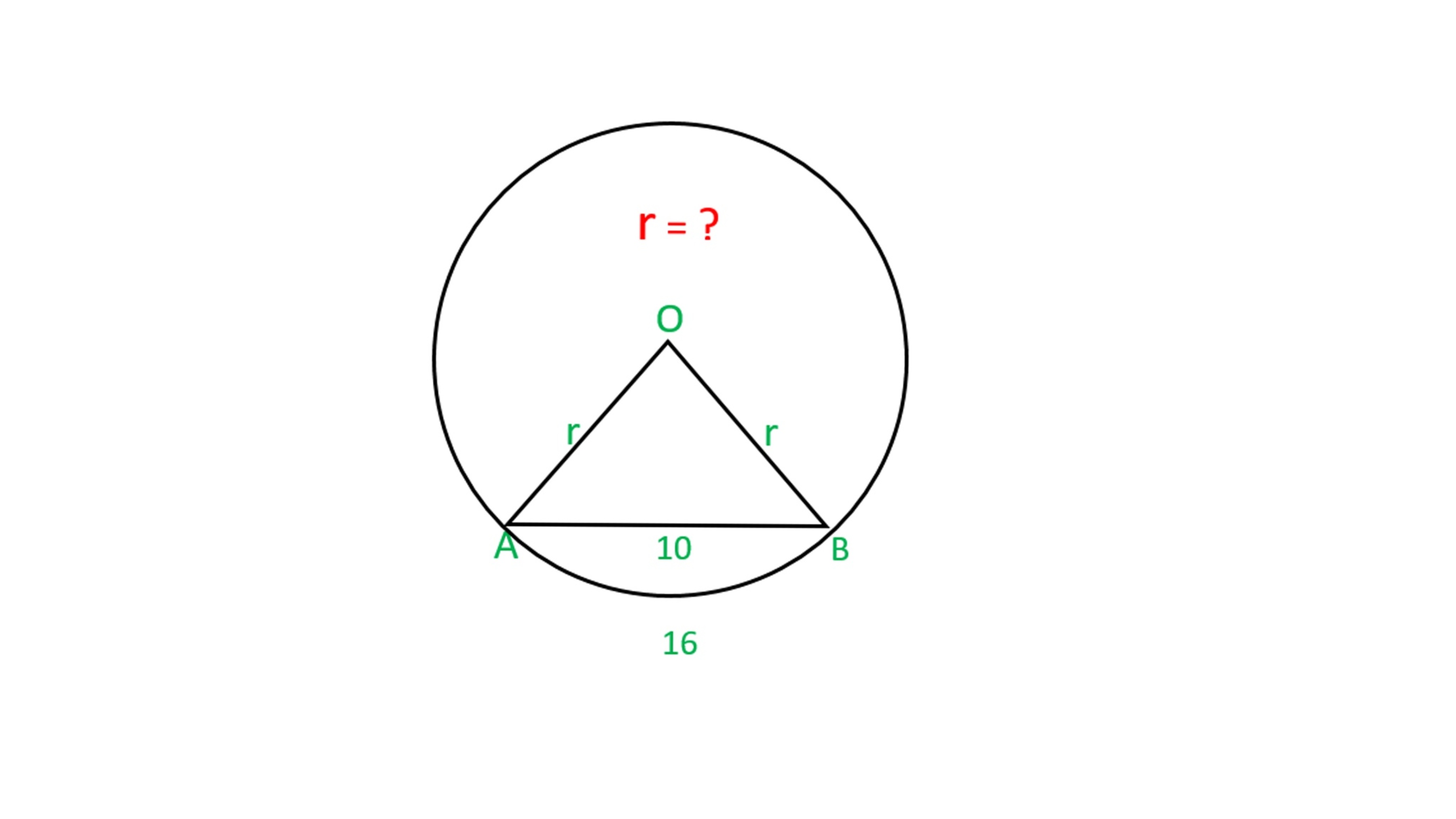
The answer is 5.02.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
sir sin works with degree angle , I mean sin(tita/2) can't be equal to 5/r it is for only degree angle
Log in to reply
I do not understand your comment. Why would sin only work for angles expressed in degrees?
Log in to reply
cause sin30'=1/2 but sin(tita) doesnot equal to 1/2 when tita is in radian, I mean sin only works with degree when ever we use ssin (redian ) in calculator, calculator convert it to redian so your equation is wrong . It is 5=r.sin(1440/(pi.r)) which is not equals to your equation.
Great explanation. I agree radians are a more natural choice of unit (they're defined in terms of arc length, after all), though I'm not sure if that's what the above comment is about.
One point on the numerical method. You can directly rearrange the equation to r = 5 cosec r 8
which suggests an iteration scheme r n + 1 = 5 cosec r n 8
for some sensibly chosen initial value r 0 .
Even with quite a bad starting point (say r 0 = 1 0 ), this is accurate to 5 decimal places after only six iterations.
I only mention this as an alternative as Newton Raphson requires calculus, which seems a little heavy-handed for this question.
This leads to a bonus question of whether all possible rearrangements of the equation lead to a convergent iteration (and if not, why not).
Log in to reply
Nice alternative method. It circumvents calculus, as you rightly have said. Thanks for sharing.
sin30'=1/2 but sin(tita) doesnot equal to 1/2 when tita is in radian, I mean sin only works with degree when ever we use ssin (redian ) in calculator, calculator convert it to redian so your equation is wrong . It is 5=r.sin(1440/(pi.r)) which is not equals to your equation.
Log in to reply
No, it is not wrong. Calculators offer the option of evaluating trigonometric ratios in radians.
sin 3 0 ∘ = sin ( 6 π ) = 2 1
When 3 0 ∘ is expressed in radians, the angle is π / 6 . Also, the definition of angle which is the ratio os arc length to radius naturally computes the angle in radians.
Log in to reply
If you change the mode to radian then calculator use the value of pi =180 if you don't change then it will use the value pi exactly and you won't get 1/2. I may be wrong so why don't you prove me wrong with your equation with mine. Here you go - you use that s=rθ when θ is radian. It's okay let me use θ as degree now s=πrθ/180 any query? now θ=180s/πr now sin(θ/2)=5/r sin(90s/πr)=5/r rsin(1440/πr)=5 which does not equal to your equation so please tell me what's wrong with my equation
Log in to reply
@Rahidul Hriddy – I do not think your reasoning is wrong. I never said so. The result you have derived is completely reasonable. The only difference between your result and mine is a scaling factor and nothing else. I did all my calculations in radian mode while you have chosen to scale your angle to degrees. Either way is fine. Try to see if you get the same result as I do, by performing the steps shown in the solution, or by applying the easier route recommended by @Chris Lewis .
Log in to reply
@Karan Chatrath – Do you mean that 1440/pi.r=8=r?
Log in to reply
@Rahidul Hriddy – No, that is not what I mean. Please read my previous comment again.
Log in to reply
@Karan Chatrath – @Rahidul Hriddy - radians and degrees are units of measurement. All the scale factor is doing is converting between them (just as you would multiply or divide by 1 0 0 to convert between metres and centimetres).
When you switch between degrees and radians on your calculator, you're telling your calculator the units you want to use. So if you ask for "sin 30" in degrees mode, it interprets the angle as 3 0 degrees. If you switch mode first, it'll interpret the angle as 3 0 radians (which is a different angle).
Trig functions like sine, cosine, tangent etc are defined in terms of ratios, so they do not have units.
So, in the previous example, if set your calculator to degree mode and type "30", then press "sin", you'll get sin 3 0 ∘ = 0 . 5 . If you now switch mode to radians, and press "asin", you will get an answer of 6 1 π = 0 . 5 2 3 5 … . This is the same angle, but in radians.
The conversion factor is 1 rad ≡ ( π 1 8 0 ) ∘ .
I hope that helps! If you have a specific question related to the problem I'll try and answer it.
Change the mode of your calculator from degrees to radians. Most scientific calculators have this option.
The angle that the arc subtends with the centre can be found using the definition of angle. Let this angle be θ . Then:
θ = r 1 6
Now, if one were to draw a line from O that intersects AB at C such that O C ⊥ A B . Then:
A C = 5 ∠ A O C = 2 θ
Now, by using the definition of sine on △ A O C :
sin ( 2 θ ) = r 5 ⟹ sin ( r 8 ) = r 5
⟹ r sin ( r 8 ) − 5 = 0
The equation above must be solved to obtain r . This is a nonlinear equation. This can be solved in an iterative method as follows. Assume the root is:
r = r o
Let:
f ( r ) = r sin ( r 8 ) − 5
It's derivative is:
f ′ ( r ) = sin ( r 8 ) − r 8 cos ( r 8 )
Use the following formula to evaluate the new estimate of the root:
r n = r o − f ′ ( r o ) f ( r o )
After getting r n , use that as the new r o and substitute it in the formula above to again obtain r n . Keep repeating this until the results of r n show repeatability. The final r n would be the answer. It comes out to be r n ≈ 5 . 0 0 2 . This is called the Newton Raphson method of solving for the roots of an equation.