Slashed Triangle

Let the side length of the equilateral triangle be 1. Then the area of the equilateral triangle is $A = \frac {\sqrt 3}4$ . Since the red line divides the equilateral triangle into two regions with equal perimeters and the two regions share a common red side, the total lengths of the blue sides of both regions are equal and is $\frac 32$ . Let the length of a blue side of the triangular region be $x$ , then the other blue side is $\frac 32 - x$ , and the area of the triangular region is $A' = \frac 12 x\left(\frac 32 - x\right) \sin 60^\circ = \frac {\sqrt 3}4 x\left(\frac 32 - x\right)$ .

The ratio of areas of the two region is:

$\begin{aligned} Q & = \frac {A'}{A-A'} = \frac {A-(A-A')}{A-A'} = \frac A{A-A'} - 1 \\ & = \frac {\frac {\sqrt 3}4}{\frac {\sqrt 3}4 - \frac {\sqrt 3}4x\left(\frac 32-x\right)}-1 \\ & = \frac 1{x^2 - \frac 32 x + 1} - 1 \\ & = \frac 1{\left(x-\frac 34\right)^2 + \frac 7{16}} - 1 \end{aligned}$

Then we have:

$\begin{aligned} \max (Q) & = \frac 1{{\color{#3D99F6}\min \left(\left(x-\frac 34\right)^2\right)} + \frac 7{16}} - 1 \\ & = \frac 1{{\color{#3D99F6}0} + \frac 7{16}} - 1 & \small \color{#3D99F6} \text{when }x = \frac 34 \\ & = \frac 97 \end{aligned}$

Therefore, $a+b = 9+7 = \boxed {16}$ .

Let $1$ be the side of the of the equilateral triangle, and $x$ and $y$ be the left and right sides of the upper triangle.

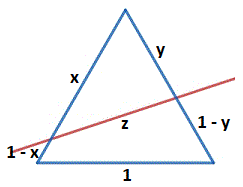
Since the perimeters are equal, $x + y + z = (1 - x) + 1 + (1 - y) + z$ , or $x + y = \frac{3}{2}$ .

The ratio of the areas is $r_a = \frac{\frac{1}{2}xy \sin 60°}{\frac{1}{2} 1^2 \sin 60° - \frac{1}{2}xy \sin 60°} = \frac{xy}{1 - xy}$

By AM-GM inequality, $\frac{3}{2} = x + y \geq 2\sqrt{xy}$ , or $\frac{9}{16} \geq xy$ , so the ratio of the areas has a maximum at $r_a = \frac{\frac{9}{16}}{1 - \frac{9}{16}} = \frac{9}{7}$ , so that $a = 9$ , $b = 7$ , and $a + b = \boxed{16}$ .

---

Bonus:

Since the areas are equal, the upper triangle is half the area of the equilateral triangle, so that $\frac{1}{2}xy \sin 60° = \frac{1}{2} (\frac{1}{2} 1^2 \sin 60°)$ or $xy = \frac{1}{2}$ .

The ratio of the perimeters is $r_p = \frac{(1 - x) + 1 + (1 - y) + z}{x + y + z} = \frac{3 - x - y + z}{x + y + z}$ .

By AM-GM inequality, $(\frac{x + y}{2})^2 \geq xy = \frac{1}{2}$ , or $x + y \geq \sqrt{2}$ , with equality at $x = y = \frac{\sqrt{2}}{2}$ . If $x = y$ , the upper triangle is an equilateral triangle, so $z = x = y = \frac{\sqrt{2}}{2}$ , so the ratio of the perimeters has a maximum at $r_p = \frac{3 - \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}} = \sqrt{2} - \frac{1}{3} \approx \boxed{1.08088}$ .