Equilateral Triangle Base-Height Rationality
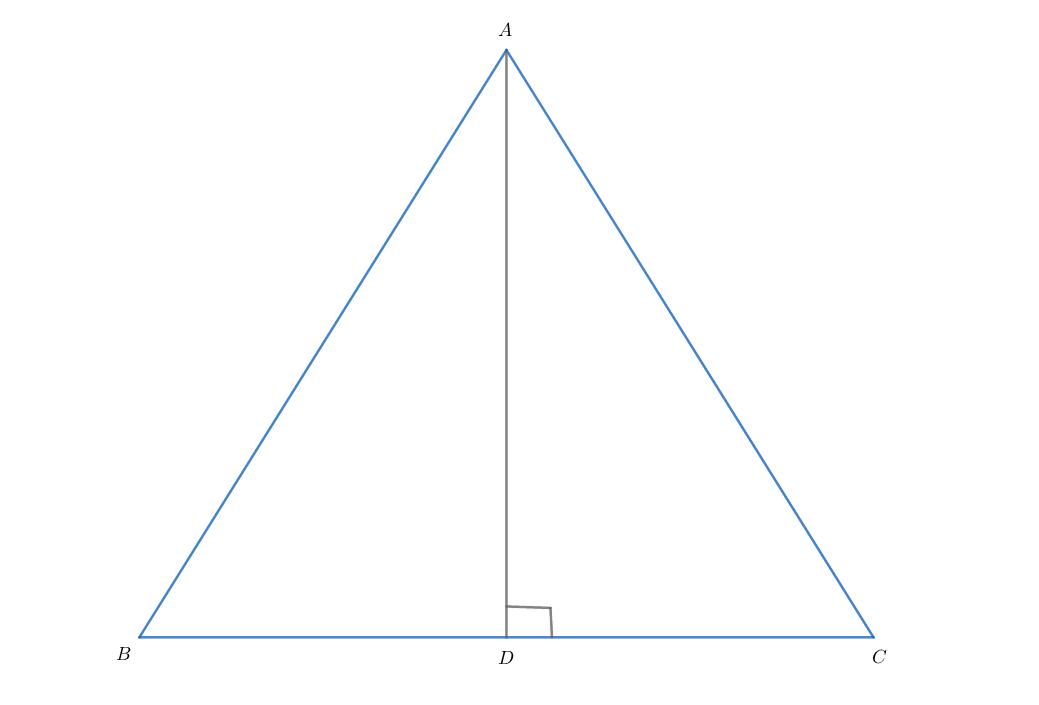
In Δ A B C , A B = B C = C A and ∠ A D B = ∠ A D C = 9 0 ∘ .
Consider the following claims about the length of A D and B C , each immediately followed by its own g r e e n Claim Value .
- Both A D and B C can be rational─ 1 .
- A D can be rational while B C can be irrational─ 2 .
- A D can be irrational while B C can be rational─ 4 .
- Both A D and B C can be irrational─ 8 .
Enter the sum of Claim Values of the TRUE claims.
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Both A D and B C can be algebraically irrational too.
Log in to reply
Correct. As long as none of them is an element of the algebraic extension Q ( 3 ) .
Log in to reply
A little bit familiar with 'field Q '. But not familiar with the notation ' Q ( 3 ) '. Would you be kind to explain?
Log in to reply
@Muhammad Rasel Parvej – Sure. Q ( 3 ) consists precisely of all numbers of the form q 0 + q 1 3 , with rational q 0 , q 1 .
In general, if R is a field and x an element not in the field, R ( x ) stands for the field of all fractions of polynomials generated by x over R , i.e. R ( x ) = { q 0 + q 1 x + q 2 x 2 + ⋯ + q m x m p 0 + p 1 x + p 2 x 2 + ⋯ + p n x n with p i , q i ∈ R } . If x is algebraic over R of order n , this field is finitely generated, since powers x n and greater may be reduced using the defining polynomial. Thus, if x is quadratic over R , we have R ( x ) = { r 0 + r 1 x , r 0 , r 1 ∈ R } .
One can add more than one element to a field in this fashion, e.g. Q ( 2 ) ( 3 ) = Q ( 2 , 3 ) consists of all expressions of the form q 0 + q 1 2 + q 2 3 + q 3 6 .
By continuing this process, one can define Q as the limit of including all quadratic irrationals, and eventually by adding the roots of all rational polynomials, one obtains Q a , the algebraic closure of Q , which contains all algebraic numbers.
(Note: The set Q ∩ R + is precisely the set of lengths that may be construed with straightedge and compass starting from a line segment of length 1.)
In the same fashion, we may define for instance, Q a ( π ) , which consists of all numbers that can be obtained by addition, subtraction, multiplication and division of rational or algebraic numbers and π ; or ( Q ( π ) ) a , which also includes numbers such as π .
Log in to reply
@Arjen Vreugdenhil – That's very kind of you! I have understood more now.
I should resume my postponed study of Abstract Algebra. Then I will come back to this.
The A D : B D is an irrational, algebraic number, namely 2 1 3 .
If A D is rational, then B C = 2 1 3 A D is irrational. Statement 1 is therefore false, and statement 2 is true.
If B C is rational, then A D = 6 1 3 B C is irrational. Statement 1 is therefore false, and statement 4 is true.
If A D is transcendental irrational, e.g. π , then B C is also transcendental, because A D and B C are related algebraically. Statement 8 is therefore true.
The total "claim value" is therefore 2 + 4 + 8 = 1 4 .