Equilateral Triangle Billiards
You are playing pool on a billiard table which is an equilateral triangle A B C . The ball is at the center of the triangle, and you hit it in any direction with uniform probability. What is the expected number of sides the ball hits before hitting side A B , to 3 decimal places?
Details and Assumptions:
- The ball bounces off the sides of the table according to the law of reflection.
- If the first side the ball hits is A B , then the number of walls the ball hits before hitting A B is zero.
- The ball is infinitesimally small.
The answer is 1.106.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The most elegant solution for sure
Typo: Line AB is parallel to Y axis.
Question: Why is it not as simple as saying: (3 + 2 + 1 + 1 + 0 + 0) / 6 = 7/6 = 1.167 ??
It obviously gives the wrong answer but why? My logic tells me if the balls has the chance of going in either of the 30 degree angle directions then it should just be the sum of the 6 divided by 6. (That is now dividing the 0 and 1 areas into two 30 degree parts)
Log in to reply
Your assumption that the demarcation between 2 and 3 bounces happens at a 3 0 ∘ -direction is incorrect.
The weights in the average are not 6 0 ∘ : 6 0 ∘ : 3 0 ∘ : 3 0 ∘ , as you suppose, but rather 6 0 ∘ : 6 0 ∘ : 4 0 . 9 ∘ : 1 9 . 1 ∘ .
Because the three-bounce scenario is less likely than you assumed, the actual expectation value is less than the value you calculated.
Let A B be on the left with B C lying horizontally at the bottom. If M denotes the midpoint of side B C and O denotes the centre of the triangle, then it is evident that the only way to obtain 3 rebounds is when the ball is hit between θ and 3 π measured anticlockwise from O M about O . Note that this can also be achieved on side A C , but due to symmetry of the two sides, this can be accounted for in the final calculation.
By forming an equation (using coordinate geometry) for the path after the second rebound, we can solve for the value of θ in
( 3 + tan ( θ − 6 π ) ) ⎝ ⎛ tan ( 4 π − θ ) + 3 tan ( 4 π − θ ) ( 6 3 tan ( θ ) + 2 1 ) + 3 ⎠ ⎞ − 3 = 0 , 0 ≤ θ ≤ 3 π
and then calculate
3 1 ( 0 ) + 2 × 6 1 ( 1 ) + 2 × 2 π θ ( 2 ) + 2 × 2 π 3 π − θ ( 3 ) ≈ 1 . 1 0 6 .
3 rebounds? I considered that impossible since there are only 2 different sides that can be hit!
Log in to reply
It can hit the same side on its first and third bounces i.e. the ball may strike the walls in the order BC, AC, BC, AB
Log in to reply
That's still only two sides: BC and AC.
Log in to reply
@Orlando Moreno – I get how you've interpreted it, but the question is intended such that any collision whatsoever increases the number of sides struck. Maybe they should have phrased it as " ... expected number of collisions ... "
Log in to reply
@Dan Ley – Or just 'expected number of rebounds'...
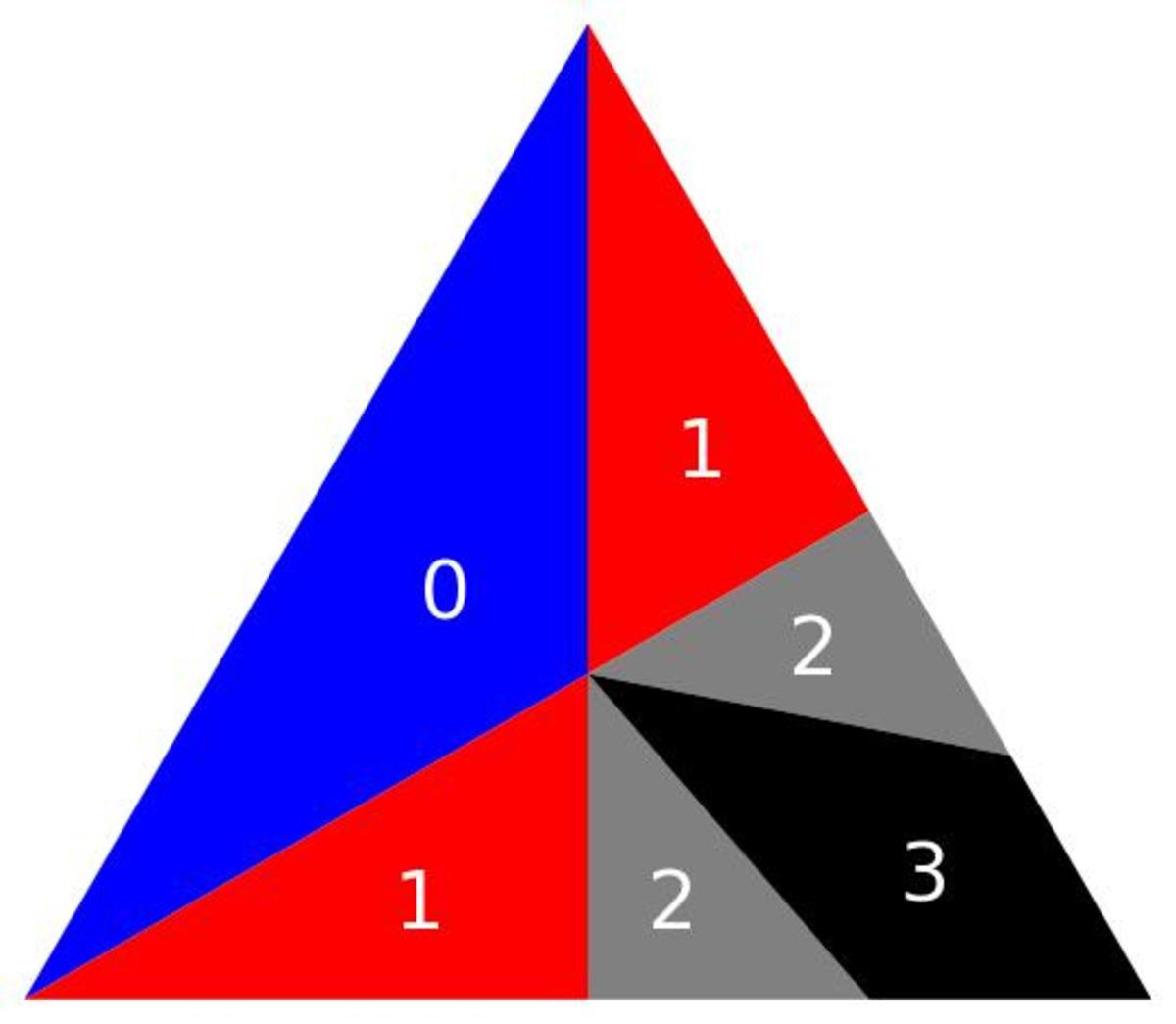
The number of bounces for each section of the table is shown. The region for zero and one hits is straightforward. The boundary between one hit and two occurs when you hit it at a midpoint. It will rebound back on itself and hit the opposite corner.
The boundary between two and three is a little more difficult. I did it algebraically, but below I outline how the geometry works out for those interested. I am assuming side lengths of one. The boundary occurs at 4 1 the length of the right and bottom sides, halfway between the midpoint and corner.
The angular spread for zero hits is 1 2 0 ° , the one hit regions each span 6 0 ° (totaling 1 2 0 ° ), the two hits regions each span 4 0 . 8 9 3 ° (totaling 8 1 . 7 8 6 ° ), and the three hits region spans 3 8 . 2 1 3 ° . The expected value for the hits therefore works out to
3 6 0 1 ( 0 ⋅ 1 2 0 + 1 ⋅ 1 2 0 + 2 ⋅ 8 1 . 7 8 6 + 3 ⋅ 3 8 . 2 1 3 ) ≈ 1 . 1 0 6
Where the three hits boundary occurs:
First, I have shown the ray that just intersects the corner when the boundary is reached.
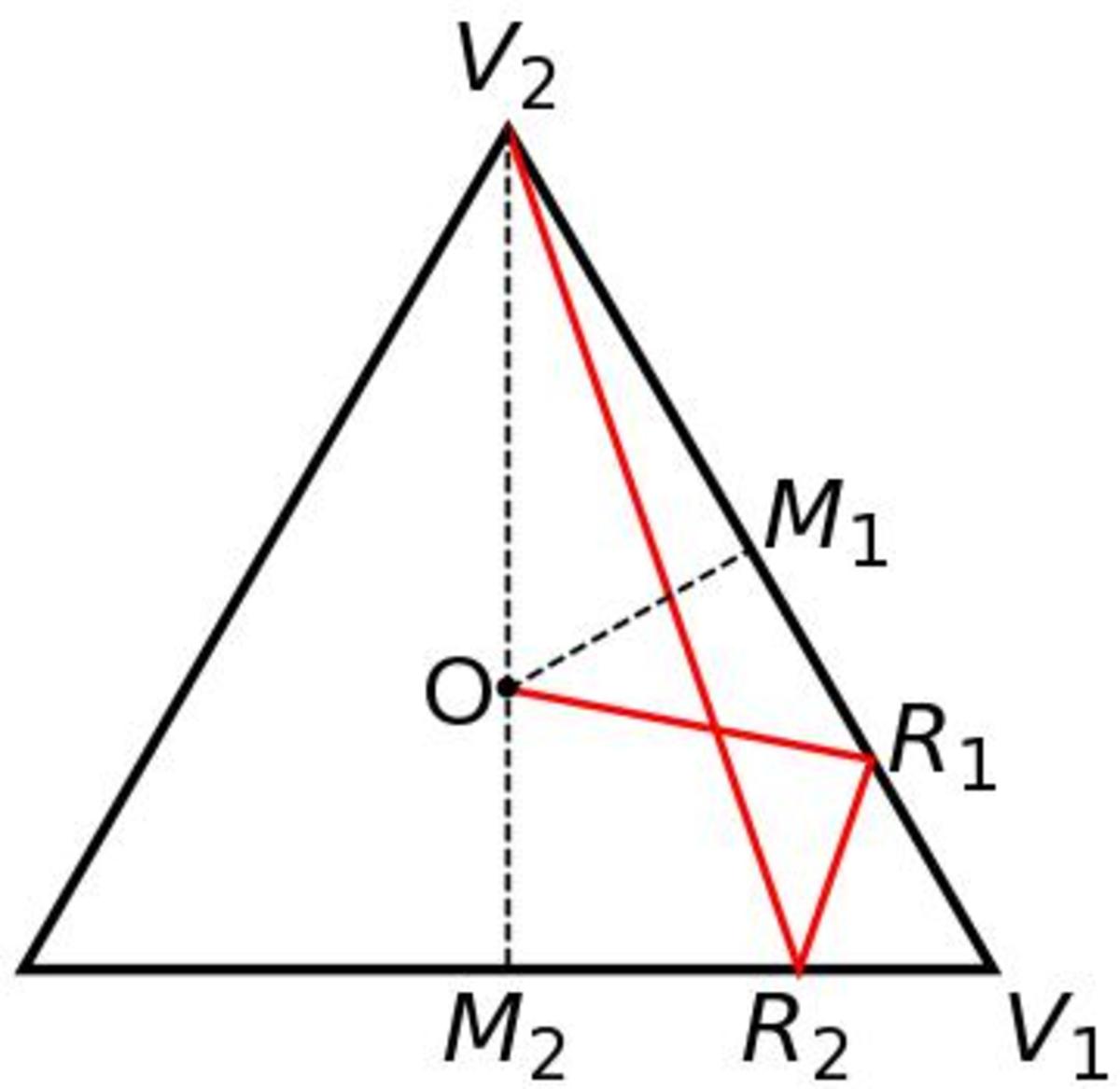
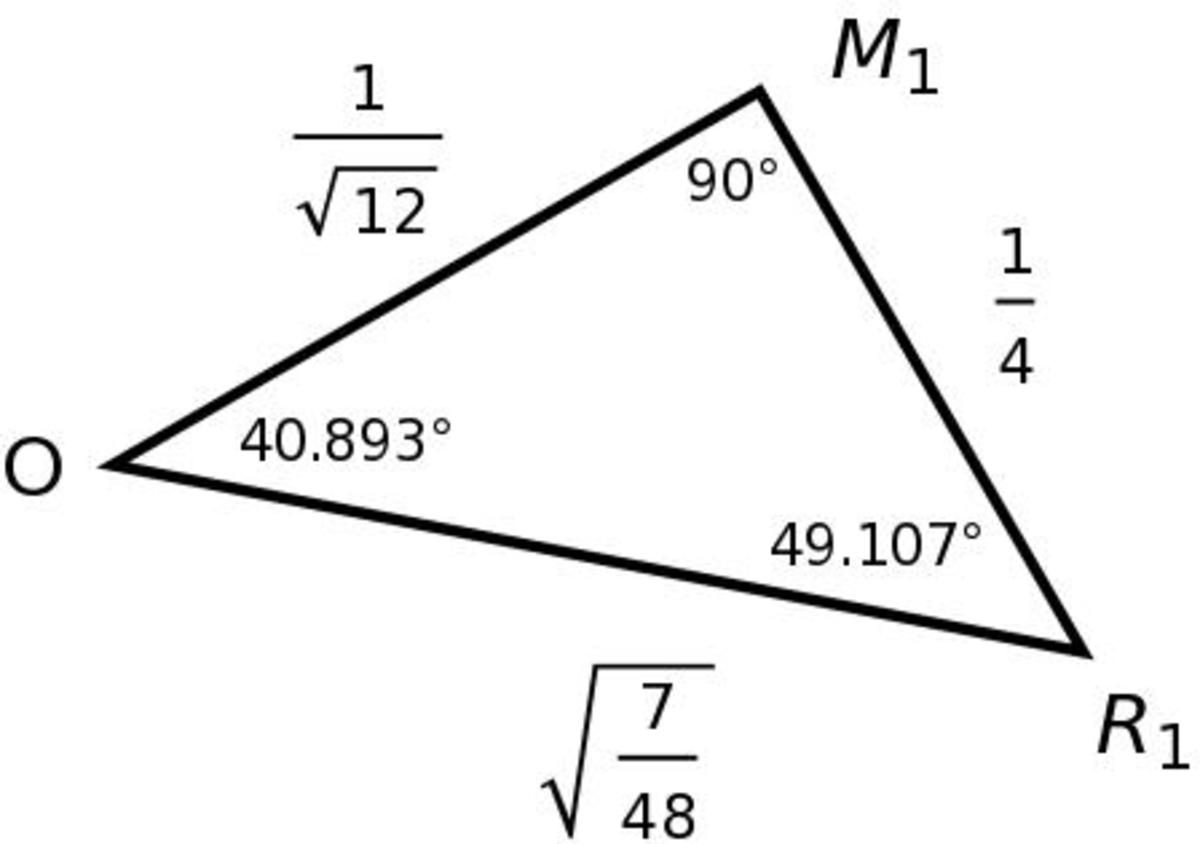
O is where the ball orginates, V 1 and V 2 are vertices, M 1 and M 2 are the midpoints of the sides, and lastly R 1 and R 2 are the points of reflection. Examining the O M 1 R 1 triangle, which was posited to have a length of 4 1 along M 1 R 1 and a given length of 1 2 1 along O M 1 . It is a right triangle so the other side length can be calculated by Pythagoras, angles given by the law of cosines. The angle of incidence θ 1 :
θ 1 = arccos ⎝ ⎛ 2 ⋅ 4 1 ⋅ 4 8 7 1 6 1 + 4 8 7 − 1 2 1 ⎠ ⎞ ≈ 4 9 . 1 0 7 °
This informs the angle of reflection in triangle R 1 V 1 R 2 . The side length R 1 V 1 is again assumed to be 4 1 . The angle at the vertex is known to be 6 0 ° . This permits the calculation of the new incidence angle 1 8 0 − 6 0 − 4 9 . 1 0 7 = 7 0 . 8 9 3 . The law of cosines once again comes into play to calculate the other side lengths, though these are not important to the problem at hand.
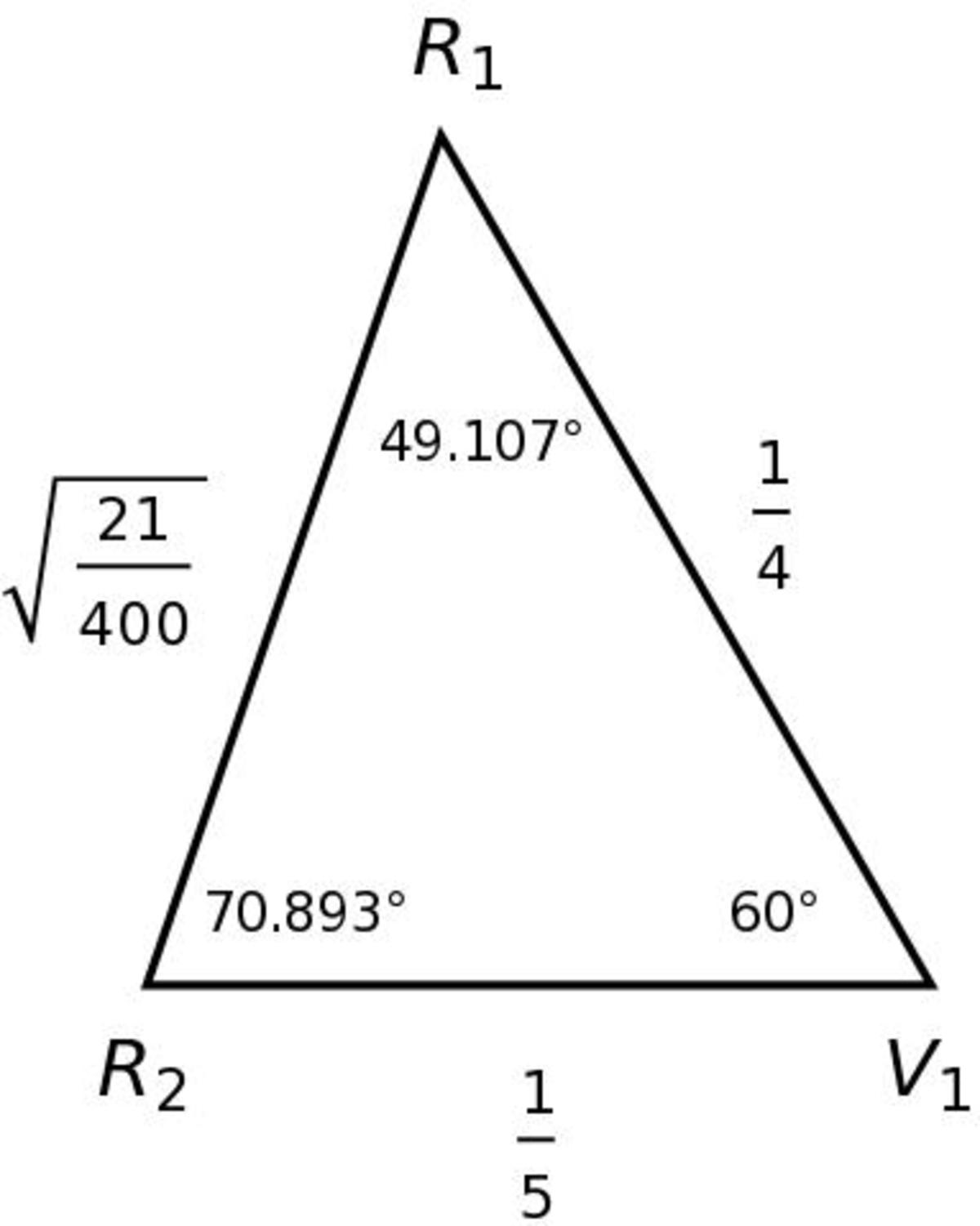
In the last triangle of interest, R 2 M 2 V 2 is a right triangle with one leg being the altitude of the whole table ( 2 3 ) and other leg length 1 0 3 . This gives the appropriate reflection angle of 7 0 . 8 9 3 ° . A ball aimed at halfway between the midpoint of a side and the corner will hit the corner after two bounces.
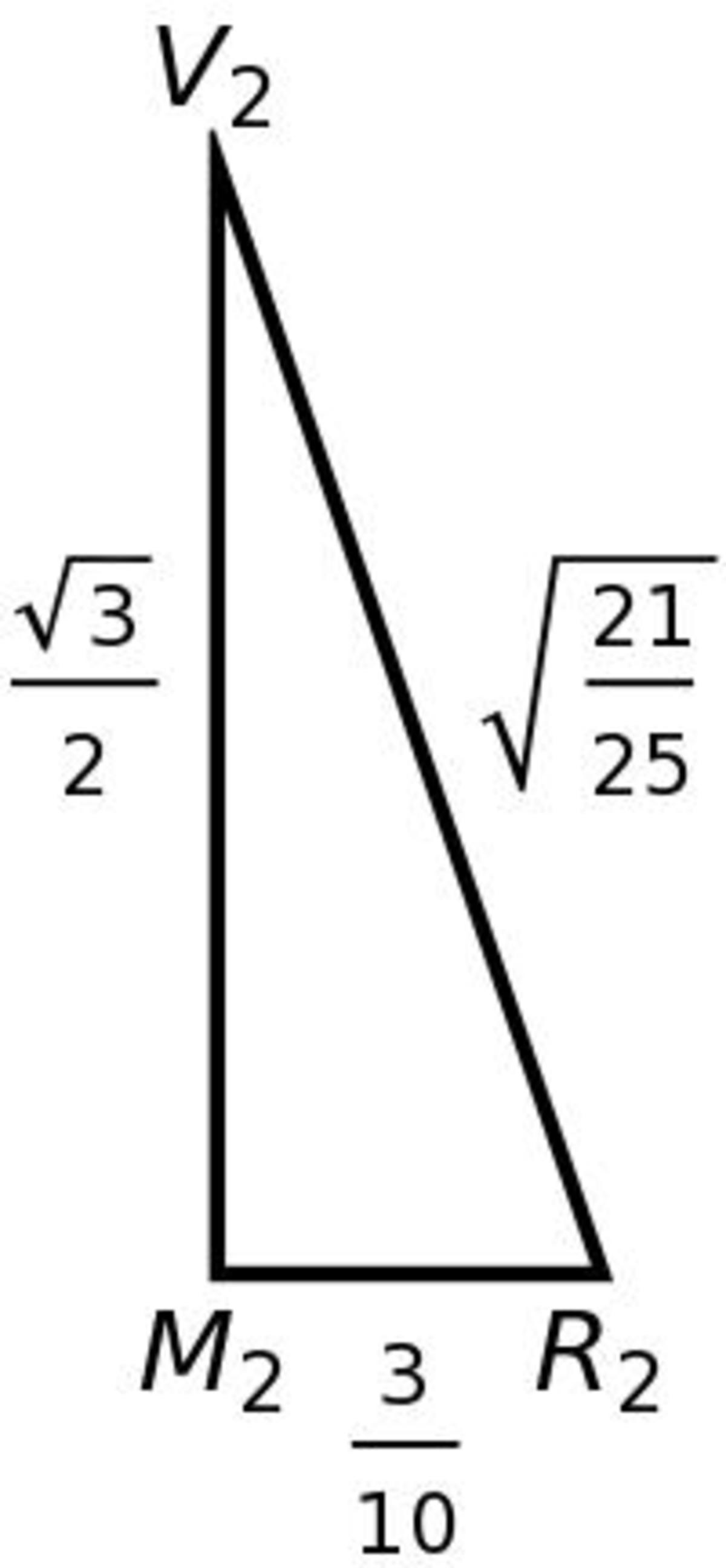
If hit more toward the corner, the ball will bounce three times before reaching the left leg. As it goes further into the corner, the triangle R 1 V 1 R 2 diminishes until the ball bounce off the corner and to the midpoint on the left leg. This I also verified algebraically, but the work is very long and tedious.
Hint: Tile the plane with equilateral triangles. Then the problem becomes looking at where a line intersects a triangular lattice. Note that when you reflect the triangle ABC, all reflections of AB form a hexagon.
The answer is
π 3 π + 2 ( − 3 2 π + π − tan − 1 ( 5 3 ) ) + 3 ( π − ( π − tan − 1 ( 5 3 ) ) ) = π π + tan − 1 ( 5 3 )
Bonus :
This problem has many extensions:
-
You can look at other shapes that tile the plane (triangle, parallelograms, hexagons). The hexagons case seems difficult.
-
Look at a circular, elliptical billiard, etc.
-
You can ask the expected time (or distance) traveled by the ball before hitting side AB. The integral is not hard but a little annoying to set up.
-
You can consider different regions on the side of the triangle for "pockets" instead of AB.
-
Look at different starting positions of the ball.
-
Look at how the expected number of sides hit or the expected distance traveled varies with the starting position.
For example, if the ball starts near C, it is easy to see that the distance traveled by the ball will be very close to the sidelength of the triangle, regardless of which direction the ball is shot in.
Edit:
Below is a graph of the expected number of sides hit (on the z-axis) versus the starting position of the ball.
A is located at ( 1 , 0 ) , B is located at ( 1 / 2 , 3 / 2 ) , and C is located at ( 0 , 0 ) .
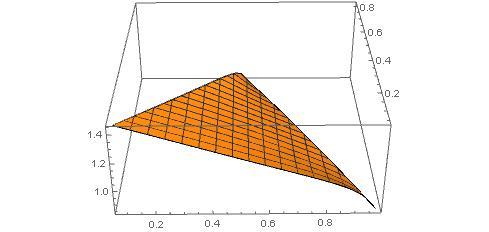
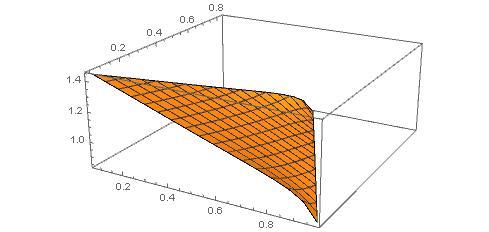
In my approach, I turn the triangle so that C is the origin of a coordinate system and A B lies to the right, parallel to the y -axis. The sides of the triangle have length 1, so that the coordinates are A ( 2 1 3 , 2 1 ) , B ( 2 1 3 , − 2 1 ) , C ( 0 , 0 ) . The ball is launched from point O ( 3 1 3 , 0 ) .
The bounces may be modeled by reflecting the billiard table in all directions, as shown below. The side A B and its reflections form a regular hexagon. The ball can be thought of as traveling in a straight line through this hexagon until it hits one of its sides.
The points of interest are P = A ( 2 1 3 , 2 1 ) ; Q ( 0 , 1 ) ; R ( − 2 1 3 , 2 1 ) .
Let the random variable Θ be the direction angle in which the ball is launched (counterclockwise, relative to the + x -axis). We limit ourselves to the upper half of the plane, as the situation is symmetric. Thus 0 ≤ Θ < π . Let B = b ( Θ ) be the number of bounces that takes place: 0 ≤ Θ < θ P θ P ≤ Θ < θ Q θ Q ≤ Θ < θ R θ R ≤ Θ ≤ π B = 0 dark green region B = 1 medium green region B = 2 light green region B = 3 white region We must determine E B = b = 0 ∑ 3 b ⋅ P ( B = b ) = 3 − ( P ( B ≤ 2 ) + P ( B ≤ 1 ) + P ( B = 0 ) ) and since P ( Θ < θ ) = θ / π this becomes E B = 3 − π 1 ( θ R + θ Q + θ P ) .
Now tan θ P = 2 1 3 − 3 1 3 2 1 − 0 = 6 1 3 2 1 = 3 ; tan θ Q = 0 − 3 1 3 1 − 0 = − 3 1 3 1 = − 3 ; tan θ R = − 2 1 3 − 3 1 3 2 1 − 0 = − 6 5 3 2 1 = 5 1 3 .
Choosing all θ s between 0 and π , we obtain θ P = inv tan 3 ; θ Q = π − inv tan 3 ; θ R = π − inv tan 5 1 3 . Thus we obtain E B = 3 − π 1 ( inv tan 3 + π − inv tan 3 + π − inv tan 5 1 3 ) = 1 + π 1 inv tan 5 1 3 ≈ 1 . 1 0 6 .