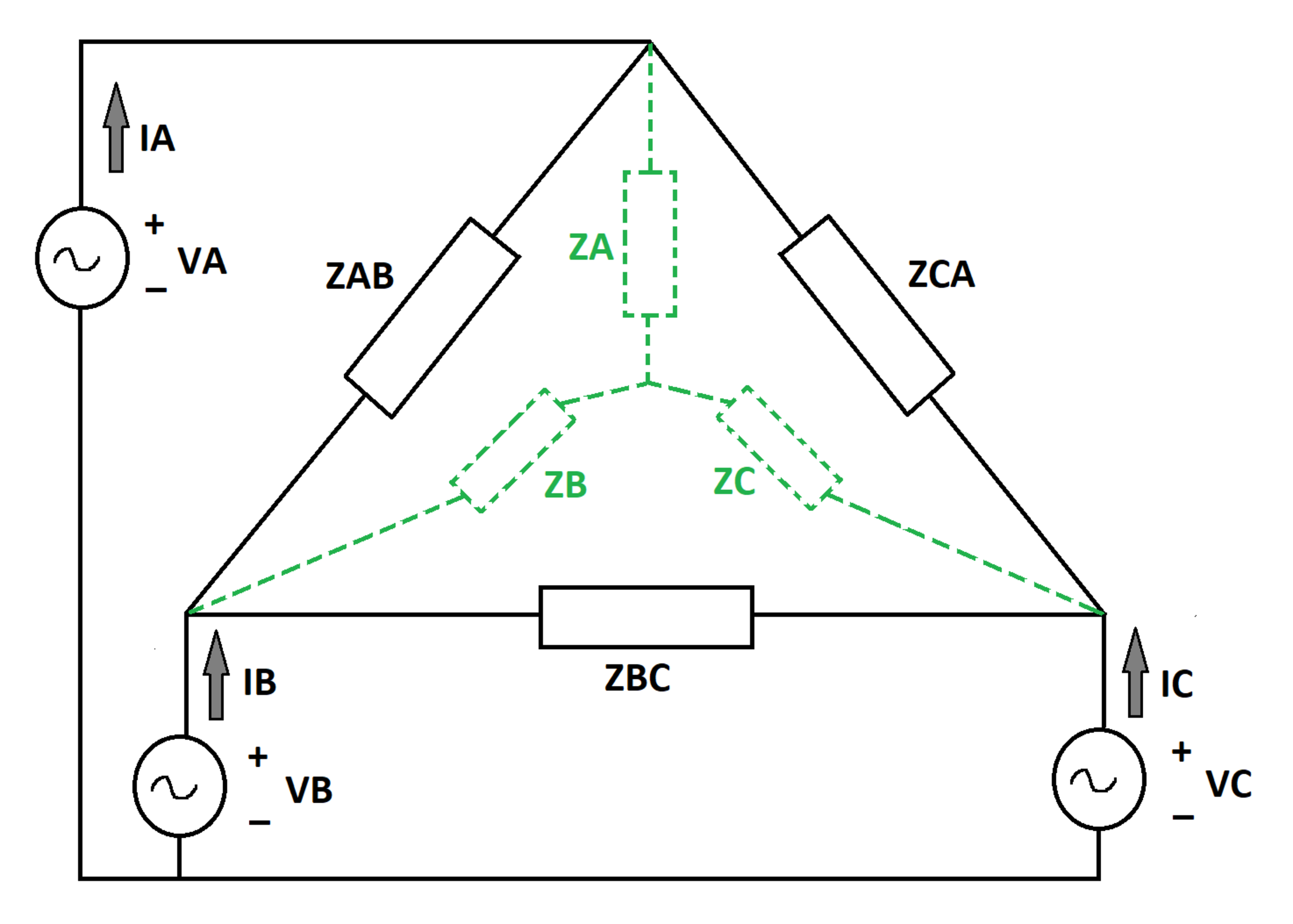
Equivalent Wye
Three AC voltage sources ( V A , V B , V C ) supply a delta-connected load consisting of impedances ( Z A B , Z B C , Z C A ) . The source currents are ( I A , I B , I C ) .
Suppose that instead of connecting the sources to the delta load, we instead connected them to a wye load (shown in green), consisting of impedances ( Z A , Z B , Z C ) .
Impose a few constraints:
C1) The wye load must draw the exact same currents ( I A , I B , I C ) as the delta load
C2) Z A = R A + j 0 (purely resistive)
C3) The resistive portions of ( Z A , Z B , Z C ) cannot be negative. Let R A m a x be the largest value of R A such that this requirement is satisfied
Let Z T = Z A + Z B + Z C . Determine the value of the following integral (read the details and assumptions carefully).
∫ 0 R A m a x ∣ Z T ( R A ) ∣ d R A
Bonus: Which value of R A corresponds to the classic equivalent wye solution ? What distinguishes the classic solution from the other solutions found in this problem?
Details and Assumptions:
1)
V
A
=
1
0
+
j
0
2)
V
B
=
5
+
j
5
3)
V
C
=
5
+
j
1
0
4)
Z
A
B
=
Z
B
C
=
Z
C
A
=
3
+
j
0
5)
The quantities mentioned in this problem are complex numbers. The quantity
j
is the imaginary unit
6)
The parentheses in the integral are there to indicate that
Z
T
is a function of
R
A
.
7)
The bars
∣
⋅
∣
denote the absolute value of a complex number
The answer is 5.609.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution. Upvoted!
How did you solved it? Using python or analytically?
If python, post you code.
Thanks in advance.
@Steven Chase
sir when I ask Karan sir for posting the solution of Ring and Magnetism he said that
“Unfortunately, for a few days from now, I will not be able to post any solutions. Also, I will have limited access to my notifications as well, in the coming days.”
I think he is busy in his life.
And when I ask Alak Bhattacharya sir he says that answer should be
2
π
B
0
R
m
g
.
Which is definitely a wrong answer and you have solved the question also.
I was solving it analytically but not able to reach the answer, can I share my approach?
I think by discussing we both can solve the problem analytically.
@Steven Chase
post the solution of your problem part 1 using python, after that i will try to solve part 2 using python.
Thanks in advance. Bye
Very nice problem!
Consider the Delta configuration. The currents through each of the three branches are I A B , I B C , I C A . Based on this, the circuit equations are:
− V A + I A B Z A B + V B = 0 − V C + I C A Z C A + V A = 0 − V B + I B C Z B C + V C = 0
According to Kirchoff's current law:
I A + I C A = I A B I B + I A B = I B C I C + I B C = I C A
Using these three equations, one can solve for I A , I B and I C . It is easy to check after solving that:
I A + I B + I C = 0
Now, consider the Y-configuration. Here, the circuit equations read:
− V A + I A Z A − I B Z B + V B = 0 − V B + I B Z B − I C Z C + V C = 0 − V C + I C Z C − I A Z A + V A = 0
Now, it is easy to see that adding any 2 of the above equations gives the third. This means that the above system of equations has infinite solutions. We use the condition that Z A = R A , plug into the result above and solve for Z B and Z C . By doing so, one gets:
Z B = ( 3 − 2 R A ) + j ( 3 R A − 3 ) Z C = ( 1 0 2 1 − 1 1 R A ) + j ( 1 0 3 − 3 R A )
Recall that all real parts of Z B and Z C cannot be negative. In other words:
3 − 2 R A ≥ 0 ⟹ R A ≤ 2 3 R A m a x = 2 3
Finally:
Z T = Z A + Z B + Z C
Here Z T is purely a function of R A . Its absolute value is also only a function of R A . The simplification to obtain this expression is left out in this solution. And the required integral is, therefore:
∫ 0 3 / 2 ∣ Z T ∣ d R A ≈ 5 . 6 0 9 2
The integral has a closed-form solution but the final computation is done using Wolfram-Alpha. I have not tackled the bonus question yet.
@Karan Chatrath
please try this problem

Log in to reply
I am having a bit of trouble with this question. Nothing is mentioned about the magnetic field, so I assume it to be a general field:
B = ( B x , B y , B z )
Let the radius of the wire be R and the current be I both of which are unknown.
Now, let the center of the wire be placed at the origin and the current flows counter-clockwise when looked at from a typical X-Y plane view.
So, an elementary arc length of the wire is:
d r = R d θ ( − sin θ , cos θ , 0 )
The magnetic force on this arc length element is:
d F = I ( d r × B )
Integrating the above components from 0 to π / 3 gives the force on the arc A B . Doing the same from 0 to π gives the total force on the wire. Let the force on arc AB be F A B and the total force be F T . It is given that:
∣ F A B ∣ = 9 ∣ F T ∣ = 8
F A B ⋅ F T = ∣ F A B ∣ ∣ F T ∣ cos ( cos − 1 ( 3 2 ) ) ⟹ F A B ⋅ F T = 4 8
So we have three equations and 5 unknowns.
Log in to reply
@Karan Chatrath but what is the answer?
Log in to reply
@Talulah Riley – I said in the beginning that I am having trouble with this question. I do not know the answer
@Talulah Riley – There are 3 equations and 5 unknowns. I do not see enough information to proceed. Unless there are implicit assumptions that I do not know of.
Log in to reply
@Karan Chatrath – @Karan Chatrath sir the magnetic field is in only one single direction.
Log in to reply
@Talulah Riley – What is the direction? Is it perpendicular to the plane of the wire? If, so, then that is stranger. Cause the angle between the force on the arc AB and the total force should be 60 degrees and not what is specified in the problem statement.
Sorry, but it seems like I don't know how to solve this.
@Talulah Riley – Could you show me how it is done? Besides, I have always asked you to share your attempt before asking me
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
i am Lil. A new guy. I don't know what you are saying to share attempt?
Ha ha joking.
Here it is
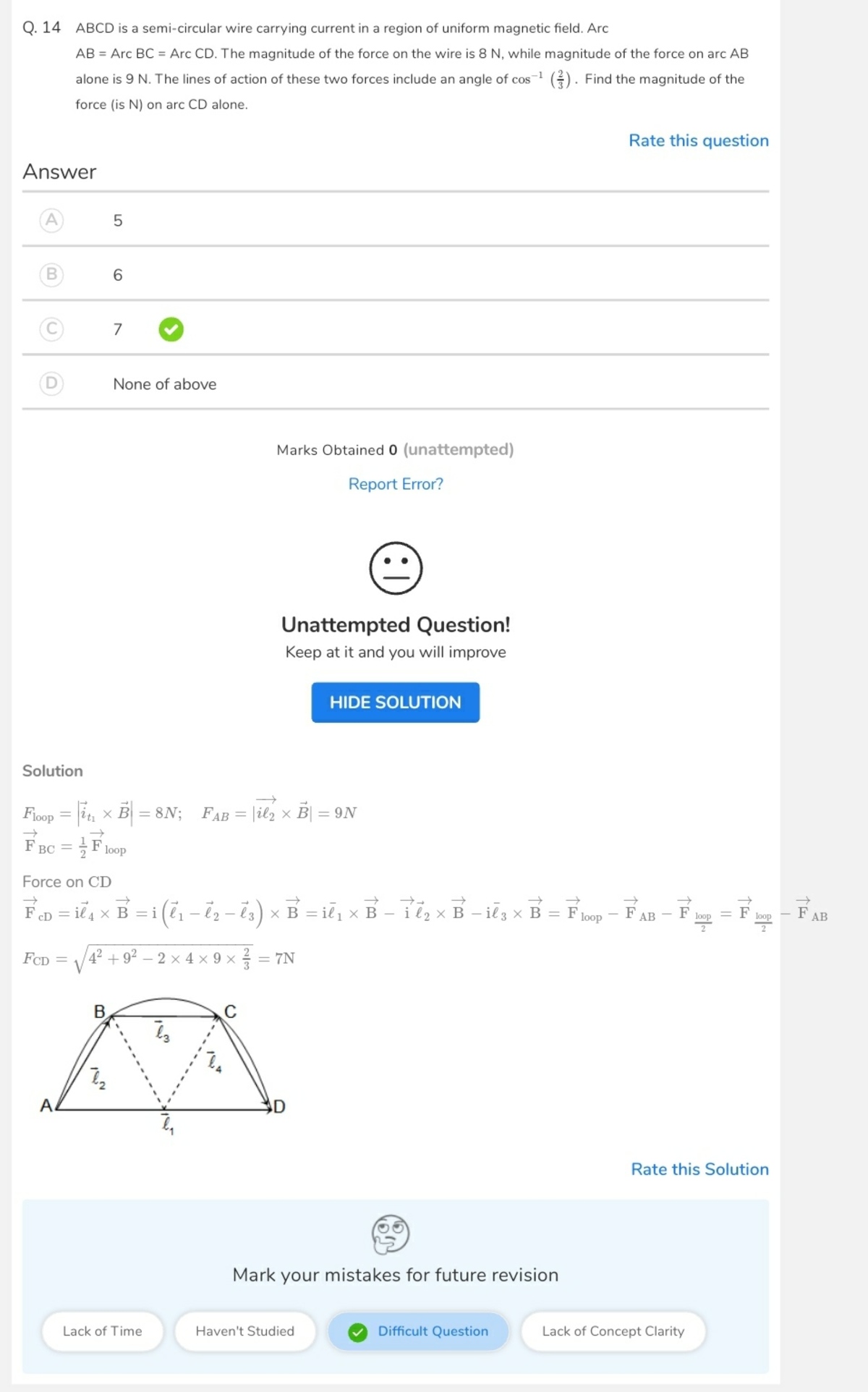
Log in to reply
@Talulah Riley – Thanks for sharing, but the font is too small
Log in to reply
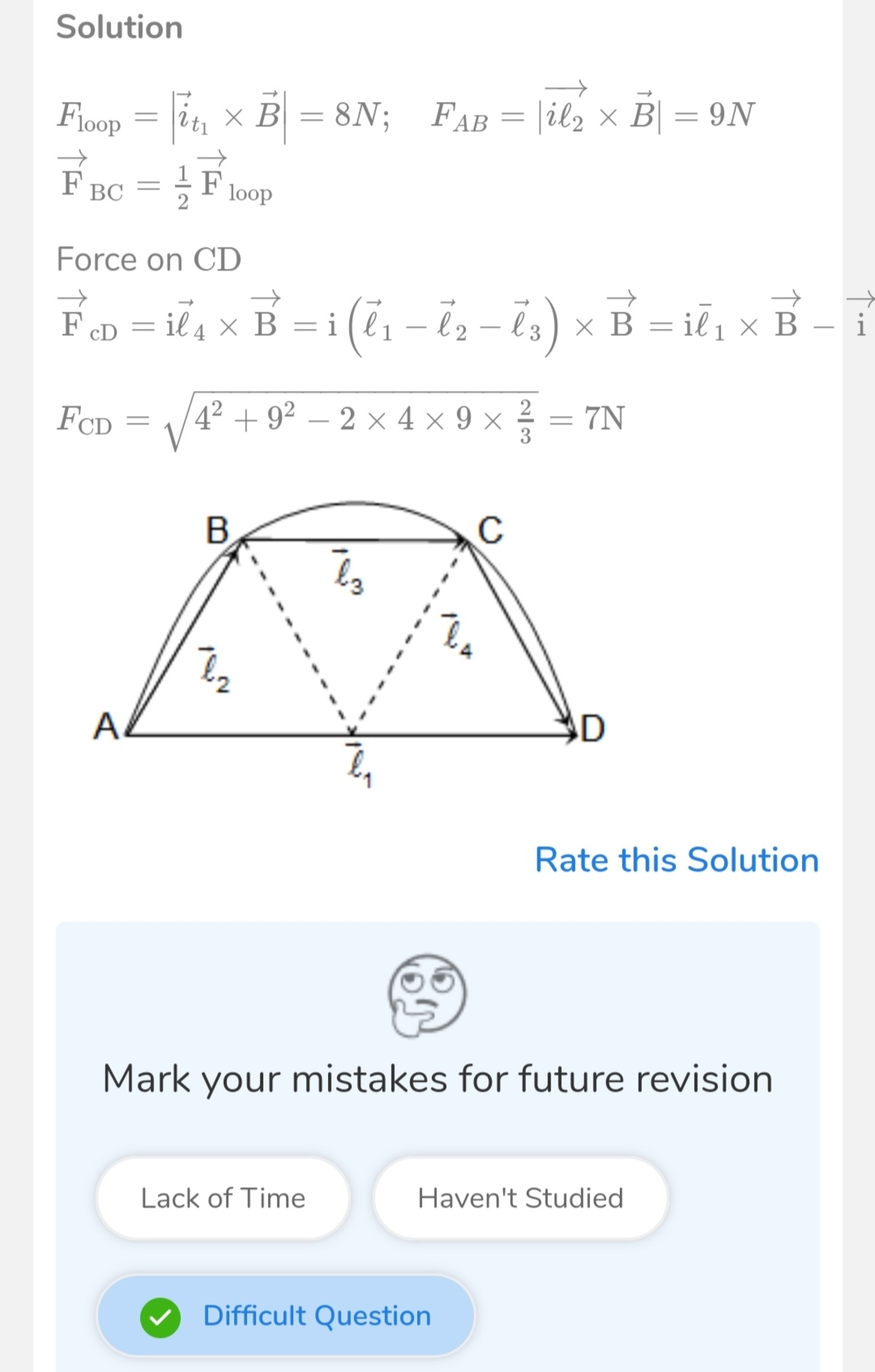
@Karan Chatrath
–
@Karan Chatrath
now I have turned off the desktop mode.
Is it clear now
As always, @Karan Chatrath has given a great solution to the problem. I will comment on the bonus. There are two ways of defining the word "equivalent" in this context:
1) A wye circuit which draws the same currents as the delta for a particular set of boundary voltages
2) A wye circuit which draws the same currents as the delta for all possible sets of boundary voltages
This problem demonstrates that there are infinitely many solutions for definition 1 . Definition 2 is much more strict, and there is only one solution in that case. The classic solution for definition 2 is Z A = Z B = Z C = 1 + j 0 , which is what you get from the formulas at the Wikipedia page. In this problem, the classic solution is the only one in which all three impedances are purely resistive.
I posted this problem because people are generally only familiar with the classic solution
I have also posted the solution code below: