Escape From The Well

The last distance the frog has to travel to escape from the well is 4 meters.

After every day, the frog climbs only 2 meters .

To climb 74 meters the frog takes 37 days.

So the frog comes out of the well on the 38th day where it climbs 4 meters

frog leap up the well forming arithmetic sequence such as : first day he reach 4 meters, second day he reach 6 meters, ..., until he escapes from the well. suppose that arithmetic sequence 4, 6, 8, ..., 78. So, n = (78 - 4)/2 + 1 = 38

everyday fog climbs up 2 meters distance in the well, so after 37 days fog had climbed up 74 meters distance and on 38th day he climbs up 4 meters so the fog comes out of the well

The frog left the watery bottom of the well more than a month ago. Mathematically he would reach the top on the 38th day at noon (assuming he sleeps midnight until whatever is the beginning of his hop-day.) In reality the frog died of dehydration and starvation somewhere around day 4 or 5 or fell back into the well where he was able to consider an alternate future with tadpoles and Mrs. Frog.

Many had post the right answer for this specific problem. BUT.

What if the frog jumped at a different height or slided less meters?

All the precedent equations would be wrong. Hence I present you the answer valid for all the frog/well problems, aka:

THE ULTIMATE FROG-WELL EQUATION

$w = j\times x - s\times x + s$

and so:

$x = (w - s) / (j - s)$

Where x=days needed, j=jump height, s=leght of the slide, w=well height

Since it come back 2m at night.The total distance the frog traveled each day is 2m. So,in 37th day the frog will reach 74m. And from that place one jump enough to reach 78m. Therefore,the frog takes 38 days to escape.

lets assume that the well is of 39 meters and the frog takes 2m to climb upwards and 1m he falls time,so in the first time he climbs to 3m mark but falls 1m and reaches to 2m mark, again second time he climbs to 4m mark but falls 1m and reaches to 3m mark.In this order,he comes out to the well in 38th attempt.

It will take 38 days. But there would only be 37 nights

Therefore 38x4 = 152 {4 m upwards during day}

37x2 = 74
{2m downwards at night}

152 + (-74) = 152 - 74 = 78

[ -74 is taken as he slips backwards at night. ]

Hence it is 38 days !

To get out of the well, the frog's distance would need to be greater than 78m, not exactly 78m, correct? Maybe on day 38 the frog reaches even with the edge and slides back that night, requiring another day to actually exit the well.

4-2=2 1 6-2=4 2 8-2=6 3 10-2=8 4 12-2=10 5 14-2=12 6 16-2=14 7 18-2=16 8 20-2=18 9 22-2=20 10 24-2=22 11 26-2=24 12 28-2=26 13 30-2=28 14 32-2=30 15 34-2=32 16 36-2=34 17 38-2=36 18 40-2=38 19 42-2=40 20 44-2=42 21 46-2=44 22 48-2=46 23 50-2=48 24
52-2=50 25 54-2=32 26 56-2=34 27 58-2=36 28 60-2=38 29 62-2=40 30 64-2=42 31 66-2=44 32 68-2=46 33 70-2=48 34 72-2=70 35 74-2=72 36 76-2=74 37 78 out 38 an = a + (n - 1)d 78 = 4 + 2(n - 1) 78 = 2n + 2 76=2n 38=n

each day the frog leaps 4 meters but falls 2 meters .so, actually each day he climbs 2 meters,

so, it should have been $\frac {78}{2} days$ =39 days

but,if we carefully look, at the 37th days he climbed = $37 \times 2$ meters =74 meters

so, the next day he will climb 4 meters and that will be 78 meters.

so, the answer will be 38 days

Here is the equation came up with for this,

4 x - 2 (x-1)=78

x is the number of days

x-1=y is the number of nights

Solution: x=38;

For the first 37 days,the frog will climb 2 m which means 74 m in total but on the last day it will climb 4 m without slipping as it has already reached the top.Thus completing 78 m in 38 days.

There is no error in the given problem. The objective is to calculate of number of days needed in order for the frog to escape.

First, identify the total height that the frog climb per day, which is 4 (going up) - 2 (slipping down) = 2 (the actual height can climb per day).

By dividing 74 meters by 2 (the actual height), you'll get 37 (this is the last day were the frog actually slipped down by night.

So by adding one more day (which represent his final climb, you'll get 38.

It's actually pretty easy let t= days for (t-1)days you will have a gain of 2 so (t-1) (4-2) is your formula for the amount of days you will have 2 then, add 4 because of the gain on the first day so, your formula is: (t-1) (distance gained in the day- distance lost at night)+distance gained on first day=total distance (t-1)*(4-2)+4=78 t=38

Hope this helps

Suppose the number of days the frog takes to climb the well be x days. Therefore, the number of nights to climb the top will be x-1. Every day he covers +4 metres. So net distance climbed up by the frog is +4x. But every night it slips -2m. So net distance it slips is -2(x-1)m. Now we know the total distance is 78m. So we add them and

+4x +(-2x+2)=78 4x-2x+2=78 2x=76 x=38 Hence the sum is solved.

78-4=74, 74/2=37, 37+1(4steps)

One can think like this:

Let frog distance per day be f(d)

• Day 1: f(1) = 4*1
• Day 2: f(2) = 4*2 - 2 One night has passed - the frog has dropped 2m.
• Day 3: f(3) = 4 3 - 2 2 Three days has passed, only two nights.

...

• Day d: f(d) = 4d - 2(d-1) = 2d - 2

So as frog escapes at 78m we get equation: f(d) = 2d - 2 = 78 Which gives us d = 38

It is simple:

$\frac{78}{2}$ -1=38

We divide it by 2 because each day he increases only 2 meters.

To climb 74 meters the frog takes 37 days.

and since it is again gonna climb a 4 meters he would have ben reached.

Let's examine the progress of the frog in the n-th day, in meters: 4, 2, 6, 4, 8, 6, 10... So, we can conclude that for every even n, An=2n and for odd n, An=2+2n. Now, because of the sequence of events (first jump 4, then fall 2), we could check if the frog got to the top on an odd n. 2n+2=78, hence n=38.

Let's say X is the number of days required by the frog to climb the well. The frog requires 4x days to achieve the goal but you need to include 2(x-1) nights while he slips away (note that the day x is the freedom day). So the equation is simply:

4x - 2(x-1)=78 x=38

Let a - be the day and night (a+4)+(a-2) = 78 2a+2 = 76 a=38

By the 37th day, the frog has made it to 74 meters. The next day, he climbs another 4 meters and gets out before he has to fall asleep and slip back again.

2(x-1)+4=78

2x-2+4=78

2x=76

X=38

He leaps 4 meters but falls 2 so average 24hours he climbs 2 meters. On the last day he doesn't sleep in the well so he doesn't fall 2 meters. So if x is the number of days it is 2 meters times the x minus 1 day(the last day the he doesn't fall) plus 4 because on the last day he gets to keep all 4 meters he climbs.

(78-2)/(4-2)=38

If you want to look at this problem using a function you can think of it like this:

1. Make a table with on the first row each consecutive day and on the second row the maximum height the frog reached that day.

1. Ignoring the first day you can see that this table follows the function $f\left( x \right)=2x+2$ (use your own method of choice to find the function rule). This function now shows us the maximum height $f\left( x \right)$ for each day $x$ .

2. We want to find out when this maximum height reaches 78 so we substitute $f\left( x \right)$ for $78$ . We find the equation $78=2x+2$ .

3. Solve this equation to find that $x=38$ .

Well considering that the last time thr frog jumps for 4 meters gets out of the well so if we take 4 of 78 There will be 74 so these need to be done by climbing 2 meters a day cause actually the last day has no sleep and going deeper but other days do have some deep going So we do this 74/2=37 days till he gets to the last jump And then the last day 1+37=38 says!!😊😊😊

You can write this problem as an equation $4x - 2 \times (x-1) = 78$

$x = 38.5$

This means that the frog Will be out during the 38th day.

Every morning the frog climbs 4 meters and night it falls two meters so for one day it climbs 2 meters in 37days the frog climbs 74 meters on the 38th day morning it climbs 4 meters and it will come out of the well

Do the math it equals 39 days

x = (78/2) - 1

OR

x = 2(78/4) - 1

An equation can also solve this: 4x - 2x = 78 --->where x means the days it takes to reach 78 meters. The solution will be: x = 39. You must take 1 from 39, because the result considers that the frog was to slip 2 meters in the 38th night - Adding 1 more day, which is unnecessary. Therefore, 39 - 1 equals to 38//

I didn't understand how 38 days I thought 39 Explain Plz

Actually... The solution would be "it doesn't escape" the frog would die at the 7th day with no food

78/2=39 days This is only if it slips down 2 meters, so take away a day, and 38

Let x be number of days and y be number of nights We know that $f(x,y)=4x-2y$ is the function describing meters up per day and meters down per night W also know that on the day Mr Froggy gets out he won't slide down at night meaning there'll always be one night less than the number of days: $y=x-1$ Solving $78 = 4x - 2(x-1)$ Gives the answer $x=38$

I deduced that the frog will probably reach the top of the well after $x$ leaps, and $x-1$ backward slides. Since he'll escape during the leap.

$4(x) - 2(x-1) = 78$

$4x - 2x + 2 = 78$

$2x = 76$

$x = 38$

Well I thought of this mathematically and logically. It can't be 39 days because of the equation I made to prove it. They say days and that means on the last day he doesn't slip two meters.

4x - 2y = 78

x being days, what we are looking for

y being nights.

If you thought of subtracting 4 - 2 and dividing it by 78, you were on the right track, except x and y (days and nights) are two different variables.

So the only reasonable answer is 38 days, not counting the extra night which would give you 39. Plugging this in the equation shows you that 38 days (and of course 37 nights) will give you 78.

4(38) - 2(37) = 78

152 - 74 = 78

78 = 78

In the last leap the frog will be out of the well

Therefore do 78-4

74 The effective leap will only be 2 as he slips at night.so 74÷2=37

37 is the total number of the leaps

Then do 37+1 as we will have to add the last. Leap

Solution is 38

Just consider the last day and you'll have the correct answer :)

In a day it climbs 4m and then slips back 2m.so for that whole 24 hours we have (4-2)m traveled..after that day there is another (4-2). So we have (4-2)+(4-2)+(4-2)+... =78 m Suppose it takes n days and n nights to travel So 4(n)-2(n)=78. So n=39.but in (4-2)+... Combination the n th term will be 80-2... If it has traveled 80 m...then we don't need another day ...so its 39-1=38

Got it in second try yo. First one was 69, second one was 38. Yee

4metres-2 metres= 2 metres climbed per day 1 day =2metres X days=78metres 2x=78 X=78/ 2 X=38 days

78/2 - 1 =38

Each 24 hours frog climbs (4-2)meters = 2 meters, but the last day when he leaps up he would reach the top and his slipping down would not count so to calculate -- (78-4)/2 + 1 = 38 days.

let n = number of days to escape

4n - 2(n-1) = 78 2n = 76 n= 38 days

What is (n-1)? Because on the last day the frog finally reach the top of the well, this lucky guy is totally free and doesn't slip backwards anymore.

It seems to be 39 days. But actually In 38th day It reaches the top of the surface.

On the last day the frog climbs his last 4 meters so 78-4=74m divide that by 2(how much it moves day by day gives you 37 days +the last day =38

38 is the day when he gets to the mouth of well. However, extra effort is required to get out from there. So ankther day should be added. The answer should be 39

Once the frog is able to get out of the well, it won't need to sleep at night and slip 2 meters backward. Let x be the number of days the frog needs. Thus our formula for the number of days it needs is:

4x - 2 (x-1) = 78 4x - 2x +2 = 78 2x = 76 x = 38

1 day only leaped 2 meters, so we left 76 meters for second day. 37 days already leaped (37*2)=74 meters, so we left 2 meters.

So, (37+1)days = 38 days ; as 2 meters per day.

Algebraically, 2(n+1)meter/days=78meter, ( n+1 )due to the calculation start from every new morning, this is because 2 is came from the resultant motion every night as +4 -2=2.

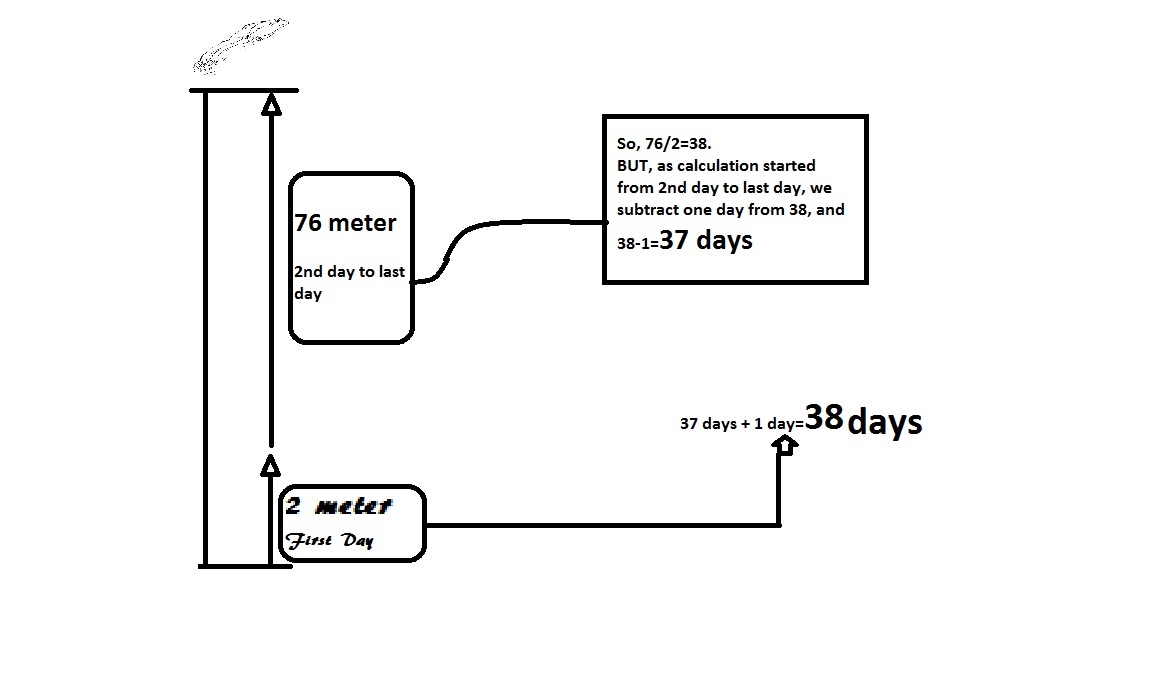
I just divided 78 by 2 then minus 1 for the last jump

He has a net gain of 2 meters a day so 78/2 = 39 -1 since on the day he escapes he gets all four meters. 38

I applied that if frog will climb 4m and slip 2m then we substract 2 from 78 and it slips 2m. So we divide it with 2.

After each 24-hour period, the frog makes only 2 meters of progress. The last day, the frog doesn't slip back because it is out of the well. 78 meters total, divided by 2 meters daily, equals 39 days if the frog slips on the last day. The frog does not slip because it is free of the well, so subtract one day from total to get the correct answer of 38 days.

After every day, the frog climbs only 2 meters, but in the last day we can to escape from the well by climbs 4 meters. So, 78 meters minus 4 meters(last day) = 74 meters. To climb 74 meters the frog takes 37 days. So the frog comes out of the well on the 38th day where it climbs 4 meters.

The frog leaps up 4 meters the first day, then slips back two meters and has to start at 2 meters on day 2. Similarly, he will start at 4 meters on day 3. He will start each day at 2(n-1) meters. This means he will start day 37 at 2(36)=72 meters and only manage to leap up to 76 meters. He'll then start day 38 at 2(37)=74 meters and make it the last 4 meters out so he won't have to slip down again. The frog therefore frees himself on day 38.

Posting this because my first answer was wrong due to sloppy thinking.

the total of his slip towards the hole is 4-2=2 ... that happens every day so 78/2=39 .. but in the day before the last day arrives to the end .. so he wont slip backwards . so the final is 39-1=38 day

Preserve 4 m up-well for the last leap, then 74 m are the in-well height to beat up 2 m a day (4 m up - 2 m down). So in-well leap need 37 days long, the next day is the last jump (4 m up-well) to reach the surface escaping from the well.

Well , the question was 'How many days' . If night was to be counted , then my answer was also right as 39 DAYS........But, the frog escapes on 38th day itself , then why he will go back into the well? But, the question was logical not scientifical . So, right answer => 38 DAYS - - -

at the last day it will go 4 meter, so before last day it will go ultimately 2meter (4-2) through day and night. so day required=(78-4)/2+1=38

Net distance = 4 meters - 2 meters Total days = (Net distance / 74 meters) - 1

How many day does the frog take to seize 78 meters if each day it leaps 4 meters up and each night he steps backwards 2 meters?

1) Since the question asks how many "day", let's substract 78meters with 2 meters which the frog goes backward a night: 78 - 2 = 76meters

2) In 1 day, the frog actually seizes only 2 meters (4 meters up, 2 meters down)

3) 76meters/2meters = 38 days.

2 meters everyday,so reaching 78 m would take 39 days.Going back to 76m which was 38th day,the frog could come out of the well by leaping 4m which is added to 76m.

Last climbing he can't down backward So he climb 74m in 37 days and 4m in 1 day. So ans. Is 38 days

the frog will reach the end on the 38th day after taking 4m from his position on the 37th day.the 2m will not be considered since he will already be ou t

2x + 4 = 78 2x = 74 x = 37 At the end of the 37th day the frog will be 4 feet from the top. One 4 foot hop takes him to the top on the morning of the 38th day

Because it travels 4 meters forward and 2 meters back, this means the frog travels 2 meters per day

78 days, 2 meters per day: 78 divided by 2 = 39.

On the last day, it doesn't fall asleep so it travels 4 meters. This means it won't need to take an extra day which means

39–1= 38 days

before reaching back to 76 he will reach 78 from 74 so 78/2 is not but 76/2 is

The distance = 78 m Daylight : up 4 m Night : down 2 m 1 day : up 2 m So : 37 days : 74 m Resume : only 4 m left to get out from the well (1 daylight only)....so the final answer is : 37+1=38 days. Cool & tricky ;)

Since the frog has an accomplishment of 2m per day, he should have finished the entire trip in 78/2 = 39 days. However, since on the 38th day, he has already reached the 74th meter mark, then there's no way he will slip since after leaping 4 meters up, he had already escaped from the well.

I just figured since it jumped 4 meters and slip 2, the total gain is 2 meters. Then I just did 78/2 = 38

I think only the answer 38 is correct not 39 ....as the distance should be always 78m. Distance covered durrind day - distance covered at night=== 78 ie the height of the well...please correct me if i am wrong

easy 2 -1 on last day. 0.5d-1

Each day the frog will jump 2 steps and reach 74 m on 37 th night and on 38 day it will jump4m and reach the top:-)

I thought 38 as well, however, it's got more logic to it than math. Very tricky

well, I think the easiest way to solve this is 78 : 2 = 39 (cause each day he can only leap 2 meters) then 39 -1 = 38 (because when he reaches the head of the well he can't slip 2 meters backwards so it won't take 1 more day!) Is there any stupid frogs to sleep when he's been out of the well?

The frog climbs up 2m per day, except for the last day where he escapes climbing up more 2m (4m), so we have:

78=2*X+2

X=(78-2)/2

X=38

last day he leaps 4 meters before he jumps out. before the last day it still need 78-4 = 74 days. everyday he only can leaps 4-2 = 2 meters. so it will take 74 : 2 = 37 days before the last day. so the total time is 37 + 1 = 38 days

I will go with Srinivas Laxmi

Key to this is noting that at the end of each DAY is when the vertical height increases by 2m, however since the frog jumped 4 meters at the end of the first day is the reason why the answer is (78/2)-1 and not just (78/2) , this is done to account for the extra couple of meters on the first day.