Escape Through Functions
A particle mass
m
=
1
k
g
is placed at
N
(
2
,
0
,
0
)
.
λ
is linear mass density.
Two graphs have the following equation:
sin
x
,
0
≤
x
≤
2
π
,
λ
=
−
1
cos
x
,
0
≤
x
≤
2
π
,
λ
=
+
1
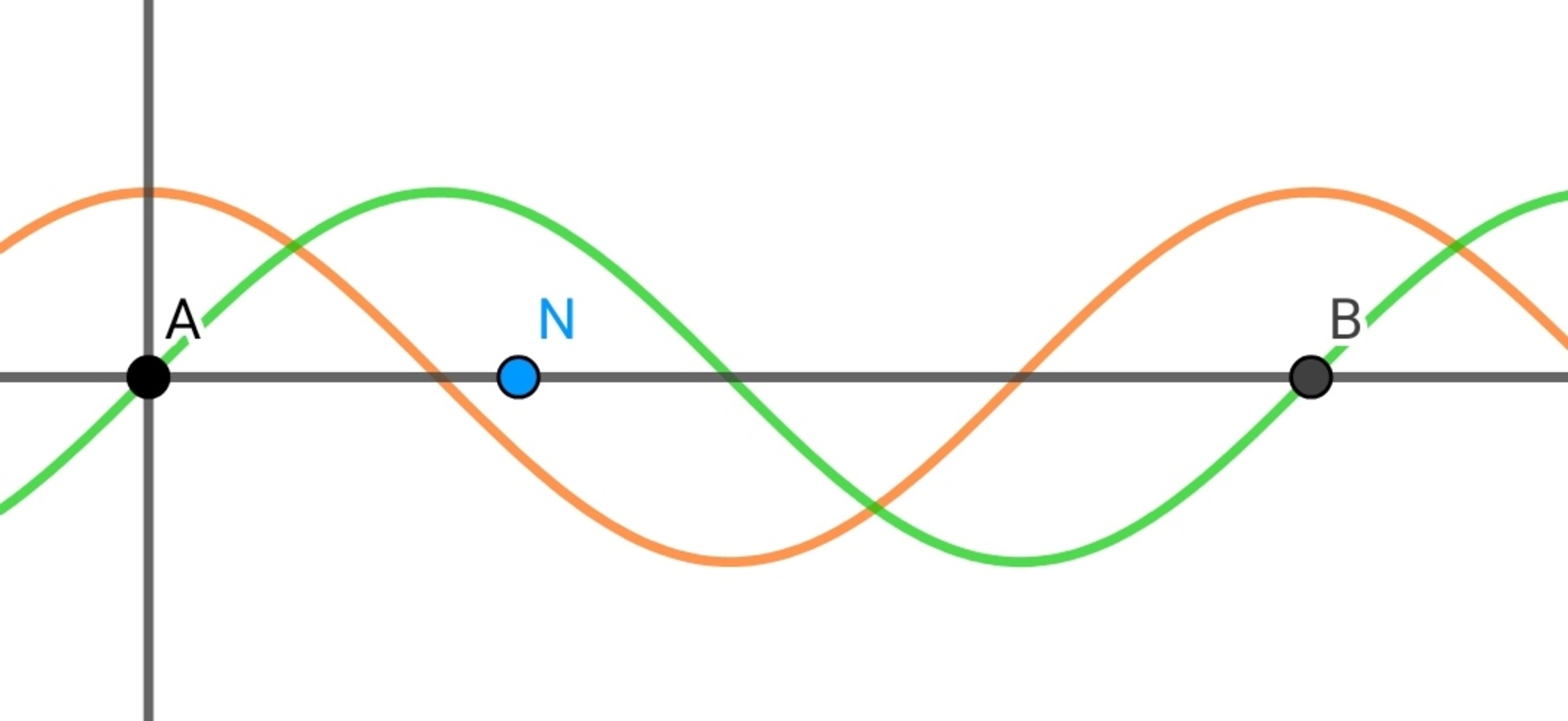
Find the speed the particle is required to escape through the field forever.
Details and Assumptions
G
=
1
(for simplicity)
The answer is 1.759.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Steven Chase Hiii Sir can we find the moment of inertia of ellipse. I am not able to find it . Le the equation of ellipse be 9 x 2 + 4 y 2 = 1 , λ = − 1 Though the vertical z axis
Sir how can you surely say that a trajectory exist such that it reaches infinite with that minimum velocity
Log in to reply
@dark angel Yes. I think in my opinion we can say. Because the particle placed here is in negative potential energy . If we provide that much of positive energy then it will neutralize each other and particle will be free from that Well. And if you give more velocity than the answer than also it will escape.
BTW, there's a python package that allows you to compute the numerical approximation of an integral .
Log in to reply
@Pi Han Goh Hii . Sir can I do this integrals in mobile also??
Log in to reply
Yes.
Log in to reply
@Pi Han Goh
–
Hii. Sir In this website where should I go to evaluate the Integrals? Well Sir please can you evaluate this integral
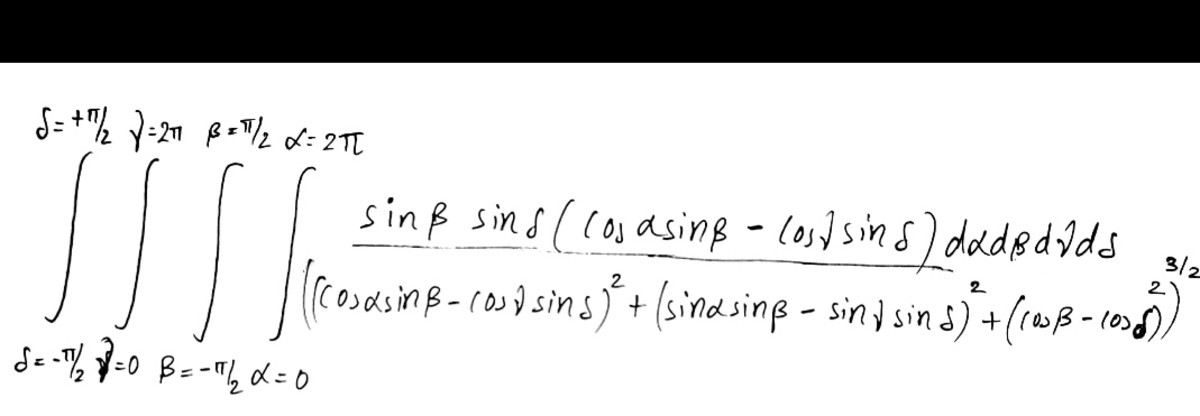
Log in to reply
@A Former Brilliant Member – Do you know how to use python? It's better to start learning how to solve simple integrals like ∫ 0 1 x 2 d x in python first, then move up to larger iterated integrals.
Log in to reply
@Pi Han Goh – No sir i don't know python,but i want to learn .Upto that level so i can evaluate that integral. . Can i start learning it in my mobile phone also??
Log in to reply
@A Former Brilliant Member – I'm pessimistic that you can learn any (decent) coding from your smartphone alone.
Try learning it on a desktop/laptop, which is much easier since you get to be more hands-on with your code.
Log in to reply
@Pi Han Goh – What Steven did is the most primitive method (I'm not saying it's bad, I just meant that there's a better way of solving it), but he gets the job done.
I would highly recommend learning Python as it's the most legible programming language out there...
Log in to reply
@Pi Han Goh – Doing it my way, I don't have to form a complicated analytical expression for the integrand. Which is often very convenient. What do you mean by "better"?
Log in to reply
@Steven Chase – Better as in "Just call the function, write the integrant and it will compute for you."
Personally, your solution seems to be unnecessarily complicated as you spliced the whole integral into many rectangles like Riemann Sum and do the whole rigmarole process.
Log in to reply
@Pi Han Goh – Not having to write the integrand explicitly makes it all worthwhile, in my opinion. Anyway, to each his own.
@Steven Chase – @Steven Chase Sir exactly we are solving physics. And we don't want to form critically hard expressions.
Log in to reply
@A Former Brilliant Member – If that's the case, then I retract what I said.
I was under the impression that the integral that we're looking for can be easily constructed.
Log in to reply
@Pi Han Goh – @Pi Han Goh which integral?
Log in to reply
@A Former Brilliant Member – The integral that gives the answer to this question? Or did I misread the question?
Log in to reply
@Pi Han Goh – @Pi Han Goh I am getting confused, time by time? Which question did you misread??
Log in to reply
@A Former Brilliant Member – Looking at Steven's solution, I was under the impression that he is computing an integral that can be expressed in simple terms, hence my very first comment above.
But Steven said that it's not necessary to do so. You even backed him up on it. So I thought I have misread this (Brilliant) problem statement. Hence, I will admit that I'm wrong and retract what I said, if I misread this (same) problem statement.
Log in to reply
@Pi Han Goh – @Pi Han Goh Sir. Oh! it is not a matter of sorry. We people are just discussing things. And I am not backed him up. I was just telling the truth. Hope you understand and I hope you, me and @Steven Chase sir will have good relationship.I think you are behaving in a sarcastic way. Cheers!
Log in to reply
@A Former Brilliant Member – Not at all. I'm just giving my two cents. Obviously there is a possibility that I misread the (Brilliant) problem statement, as I'm not so good in physics.
Take care!
Log in to reply
@Pi Han Goh – @Pi Han Goh Sir which (Brilliant) problem statement? I think there is no statement in problem in which we have to follow a particular method , we can solve it from anywhere using analytical method or code.
Take care!
Log in to reply
@A Former Brilliant Member – Brilliant problem statement = Find the speed the particle is required to escape through the field forever.
I do not particularly care how it was solved actually....
Log in to reply
@Pi Han Goh – @Pi Han Goh Sir so which problem statement you were talking about from last 1 hr ? I think this discussion between us is the most critical discussion of my whole life.
@Pi Han Goh
–
@Pi Han Goh Ok Sir I just installed a python app from google play store and try to integrate your expression but can't get the answer
3
1
Here is my work.

Log in to reply
@A Former Brilliant Member – You need to install the scipy python package first. The online compiler on this site wouldn't do.
I'd suggest that you start from the ground up and install your own IDE, like VScode or Sublime on your computer.
I'm not sure if there's any IDE that is suitable for tablet / smartphones.
@A Former Brilliant Member – Also, it's
1 |
|
>> Steven used an older /archaic Python version, so he is able to run this code.
Log in to reply
@Pi Han Goh – Also, if you just started learning L A T E X , I would recommend that you start doing simple things like creating loops and modifying lists and dictionaries.
Don't go into the deep end first by solving integrals in Python immediately.
you said: "Sir so which problem statement you were talking about from last 1 hr ? I think this discussion between us is the most critical discussion of my whole life."
The problem statement that I'm referring to all along is "Find the speed the particle is required to escape through the field forever."
Like I said, I'm under the impression that the integral needed to solve the problem statement can be expressed in simple terms, hence my very first comment above: "BTW, there's a python package that allows you to compute the numerical approximation of an integral ."
Log in to reply
@Pi Han Goh Okayy!! Finaly I got it! BTW. Sir can you parametrise the ellipsoid , and what will be its d A area??
Log in to reply
I'm sorry, I'm not able to help you. My grasp of the science concepts isn't strong, I'm afraid that I might unintentionally give you a wrong answer.
Log in to reply
@Pi Han Goh – @Pi Han Goh Okay No problem. In which field you are strong because,I have doubts in all field in maths and science. Then I will ask??
@Pi Han Goh my line which you have highlighted above. I was just kidding. Don't take it seriously. C h e e r s !
Log in to reply
No problem at all!
Log in to reply
@Pi Han Goh – @Pi Han Goh Okay No problem. In which field you are strong because,I have doubts in all field in maths and science. Then I will ask??
Log in to reply
@A Former Brilliant Member – Pure recreational math.
Log in to reply
@Pi Han Goh
–
@Pi Han Goh
I have not heard of this topic yet. I think its related to entertainment. But I will try my best. Here is the question.

Log in to reply
@A Former Brilliant Member – Recreational math = Mainly math puzzles, mixed with some basic undergraduate algebra, probability, statistics, number theory, and some calculus.
SInce g ( x ) : = ( x − 2 ) 5 + 3 ( x − 4 ) 7 is an increasing and continuous function for x > 0 , then − 2 = f ( 3 ) < f ( x ) < f ( 5 ) = 2 4 6 .
Thus, all the integer values of ⌊ g ( x ) ⌋ = f ( x ) are − 1 , 0 , 1 , … 2 4 5 . The answer is (d) .
You can visualize the graph of f ( x ) by first plotting in Desmos .
Log in to reply
@Pi Han Goh – @Pi Han Goh thanks for the solution. I have one more question [ 4 , 3 , 2 , 1 , 3 , 2 , 3 , ? ] Fill the question mark??
Log in to reply
@A Former Brilliant Member – I personally hate all this "what comes next?" type of question, because there are no real fixed rules to questions like this. So I'm afraid I won't be giving a proper answer to this question.
Log in to reply
@Pi Han Goh – @Pi Han Goh Yes because it has upto infinte variations. But I will give you hint. Hint- (This question is related to you. Your identity)
Log in to reply
@A Former Brilliant Member – Once again, I'm opting not to answer questions like this, as it doesn't interest me.
Log in to reply
@Pi Han Goh
–
@Pi Han Goh
okay sorry.

Log in to reply
@A Former Brilliant Member – Hi Neeraj, I don't mean to sound dismissive or rude here, but this site is not a place for you to post your homework questions (or equivalent) without showing any attempts.
If you would like to ask how to solve a question, try posting it here , and make sure you show the attempts that you have done and show where you are stuck.
For this latest question, consider Descartes' rule of signs .
Nice problem. However, I find the notion of 'negative mass' difficult to interpret.
Consider the curve y 1 = sin x . Mass of an elementary arc length near a point ( x , y 1 ) is:
d m 1 = − d x 1 + cos 2 x
Gravitational potential energy due to this element is:
d V 1 = − ( x − 2 ) 2 + y 1 2 G m d m 1
Same for the curve y 2 = sin x . Mass of an elementary arc length near a point ( x , y 2 ) is:
d m 2 = d x 1 + sin 2 x
Gravitational potential energy due to this element is:
d V 2 = − ( x − 2 ) 2 + y 2 2 G m d m 2
Potential energy due to both elements:
d V = d V 1 + d V 2 = ⎝ ⎛ ( x − 2 ) 2 + sin 2 x 1 + cos 2 x − ( x − 2 ) 2 + cos 2 x 1 + sin 2 x ⎠ ⎞ d x
Total potential energy due to both curves is:
V = ∫ 0 2 π ⎝ ⎛ ( x − 2 ) 2 + sin 2 x 1 + cos 2 x − ( x − 2 ) 2 + cos 2 x 1 + sin 2 x ⎠ ⎞ d x
Now, for the particle to just escape the gravitational field, it must be projected with a speed such that its final energy becomes zero. Applying the energy conservation principle gives:
V + 2 v 2 = 0 v = − 2 ∫ 0 2 π ⎝ ⎛ ( x − 2 ) 2 + sin 2 x 1 + cos 2 x − ( x − 2 ) 2 + cos 2 x 1 + sin 2 x ⎠ ⎞ d x ≈ 1 . 7 6
@Karan Chatrath Ha Ha Ha well! I doesn't know much about negative mass. Why does you feel negative mass difficult to interpret?? Well the real story is that i was making this question for Electricity and magnetism. After that i think if I place positive and negative charge. Can we write net electric potential equal to kinetic energy of that particle. In that case I have to give mass of particle also???
Log in to reply
Mass is a way of quantifying the amount of matter contained by anything. A mass of zero indicates the absence of any matter in a given space. So what does a negative mass physically indicate? I do not know..
Log in to reply
@Karan Chatrath Sir if I say you that it's compulsory say 2-3 line on negative mass. Let we consider that negative mass exist, then what it would be. First you share your opinion with me then I will share with you. @Steven Chase Sir you are also welcome to share your opinion and it's compulsory. N o E x c u s e Later on I will share my official opinion.
Log in to reply
@A Former Brilliant Member – Operationally, if you push on a negative mass, it accelerates in a direction opposite to your push.
Log in to reply
@Steven Chase – @Steven Chase Okay! That looks weird. Well! Can you give me physically feel??of negative mass
@Karan Chatrath Can you help me in finding the moment of inertia of ellipse about z axis?
Nice problem. Simulation code is attached. Note that the net graviational potential energy is negative, which means that the particle has to have positive initial kinetic energy in order to escape the system.