Euclid's Riddle II
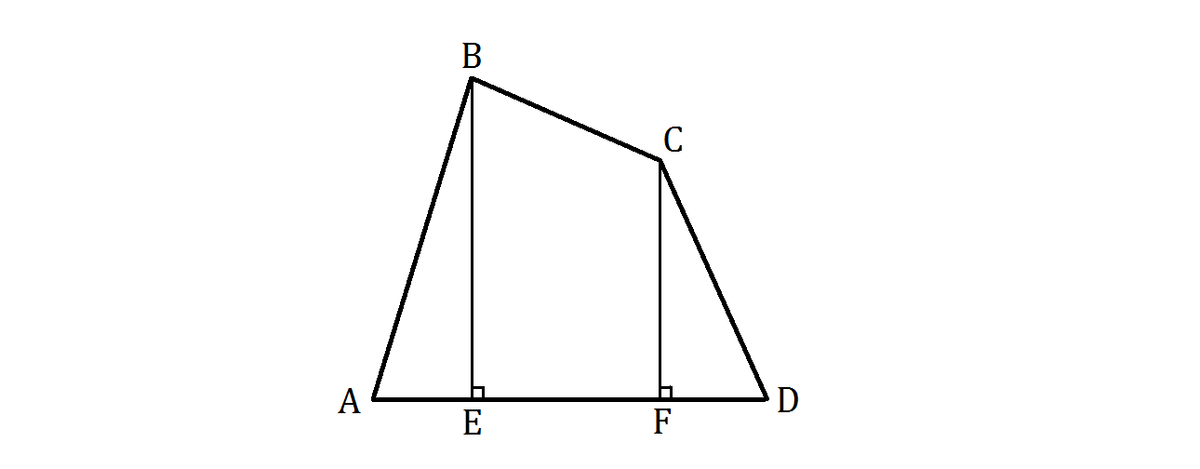
Euclid was given order to measure the area of the quadrilateral A B C D , where he drew perpendicular lines ( B E & C F ) to the base A D , as shown above.
Euclid : This bizarre-looking shape has no integer side length except for its base ( A D ). But no despair. Fortunately, the new lines ( B E & C F ) here have the lengths of some integers. Now thou will measure and tell me their relationship.
Pupil : B E + C F = 2 A F , and A F is a multiple of F D , master. Still, how shall we calculate its area, my teacher?
Euclid then extended the new (red) lines to meet at point G , as shown below:
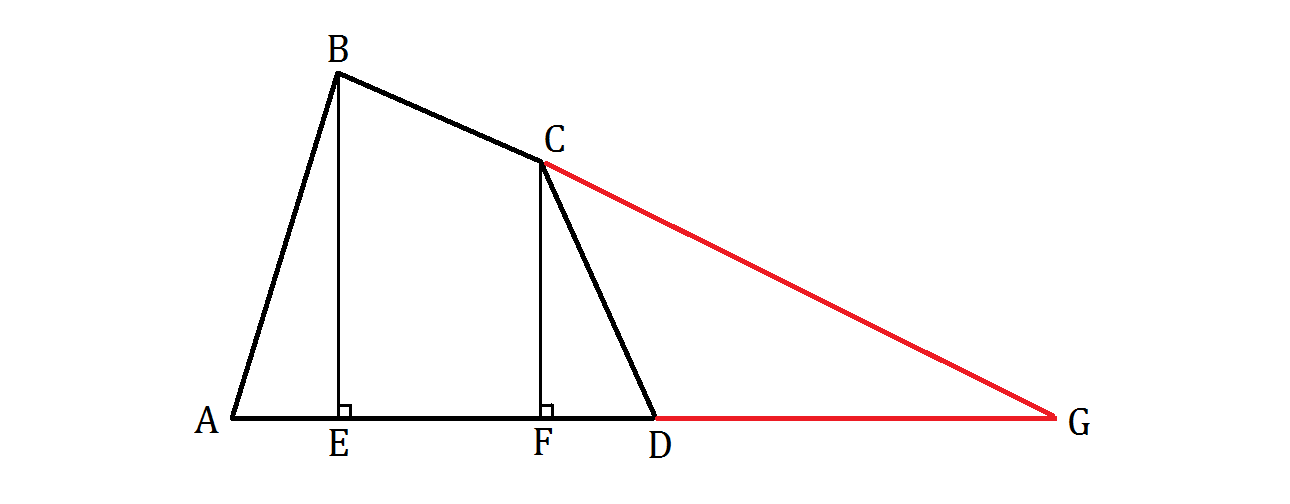
Euclid : Now measure these new (red) lines. What can thou deduce from all these segments?
Pupil : A F + F C = C G , and they are all pairwise co-prime. Also, A D = D G , master.
Euclid : Alas! At last, the solution stands before our eyes. What is the area of this quadrilateral A B C D ?
The answer is 72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Considering the right triangle C F G , it has all integer side lengths, making them Pythagorean triples. Then suppose C F = a ; F G = b ; and G C = c for some integers a , b , c .
From the first part, we know that A F = C G − F C = c − a .
Let then B E = h , and h + a = 2 ( c − a ) . h = 2 c − 3 a .
We also know that h > a , so 2 c − 3 a > a . Hence, c > 2 a .
The upper bound of h happens when we create the triangle A H G to C F G with ∠ H A G as a right angle.
Then with similarity ratio, A H = h m a x = b a ( A H ) = b a ( c − a + b ) > h .
Thus, b a ( c − a + b ) > 2 c − 3 a .
a c − a 2 > 2 c b − 4 a b
4 a b − a 2 > c ( 2 b − a )
2 b − a 4 a b − a 2 > c
2 a + 2 b − a a 2 = a ( 2 + 2 b − a a ) = a ( 2 + 2 a b − 1 1 ) > c
Since b > a , then a b > 1 .
a 2 b − 1 > 1 .
Thus, 2 a b − 1 1 < 1 , and a ( 2 + 2 a b − 1 1 ) < 3 a .
Therefore, 3 a > a ( 2 + 2 a b − 1 1 ) > c > 2 a . In other words, 3 > a c > 2 .
Now from F D ∣ A F , we can rewrite as: 2 a + b − c ∣ c − a . According to Euclid's formula, we can parametize c = m 2 + n 2 ; a = 2 m n or b = m 2 − n 2 or vice versa, depending on which one is even for some co-prime integers m > n .
Then 2 m 2 − n 2 + 2 m n − ( m 2 + n 2 ) ∣ c − a .
m n − n 2 ∣ c − a .
n ( m − n ) ∣ c − a .
For odd a = m 2 − n 2 , c − a = 2 n 2 . Then m − n ∣ 2 n . Since m − n is odd, then m − n ∣ n .
Hence, k ( m − n ) = n for some integer k . k m = ( k + 1 ) n . However, g c d ( k , k + 1 ) = 1 for any k , so k ∣ n . And since g c d ( m , n ) = 1 , then n ∣ k .
That means n = k and m = k + 1 = n + 1 .
Returning to the inequality 3 > a c > 2 , we can substitute in terms of m , n :
3 > m 2 − n 2 m 2 + n 2 > 2 . Then 3 > ( n + 1 ) 2 − n 2 ( n + 1 ) 2 + n 2 > 2 .
3 > 2 n + 1 2 n 2 + 2 n + 1 > 2 .
2 > 2 n + 1 2 n 2 > 1
Solving for each side, 2 n 2 > 2 n + 1 . 2 n 2 − 2 n − 1 > 0 . Solving the quadratic formula, we will obtain n > 2 1 + 3 ≈ 1 . 3 7 or n ≥ 2 .
On the other hand, 2 ( 2 n + 1 ) > 2 n 2 . 0 > n 2 − 2 n − 1 . Solving the quadratic formula, we will obtain n < 1 + 2 ≈ 2 . 4 1 or n ≤ 2 .
The only possible value is n = 2 and, thus, m = 3 , and Pythagorean triple of ( 5 , 1 2 , 1 3 ) . However, with this, h = 2 c − 3 a = 2 6 − 1 5 = 1 1 , but 1 1 > h m a x = b a ( c − a + b ) = 1 2 5 ( 1 3 − 5 + 1 2 ) ≈ 8 . 3 3 , which is not applicable.
That means a = 2 m n is even, and so n ( m − n ) ∣ c − a = ( m 2 + n 2 ) − 2 m n = ( m − n ) 2 . Hence, n ∣ m − n and n ∣ m .
The only applicable value is n = 1 .
Then similarly for the inequality 3 > a c > 2 , we can substitute in terms of m , n :
3 > 2 m m 2 + 1 > 2 .
Solving for each side, m 2 + 1 > 4 m . m 2 − 4 m + 1 > 0 . Solving the quadratic formula, we will obtain m > 2 + 3 ≈ 3 . 7 3 or m ≥ 4 .
On the other hand, m 2 + 1 < 6 m . m 2 − 6 m + 1 < 0 . Solving the quadratic formula, we will obtain m < 3 + 2 2 ≈ 5 . 8 3 or m ≤ 5 .
Only m = 4 , 5 works, but since n = 1 is odd, then m must be even and equals to 4 .
That leads to the Pythagorean triple of ( 8 , 1 5 , 1 7 ) . h = 2 c − 3 a = 3 4 − 2 4 = 1 0 .
A F = 9 . F D = 2 9 + 1 5 − 9 = 3 , and 3 ∣ 9 . A G = 2 4 , and D G = 1 2 .
Finally, the area of the quadrilateral A B C D = 2 1 0 ( 2 4 ) − 2 8 ( 1 2 ) = 1 2 0 − 4 8 = 7 2 .
Let me do say that this problem has been a particularly awkward one. Like trying to untangle an horrific knot of Xmas lights.
Log in to reply
Oh...is it too hard to understand?
Log in to reply
There's nothing wrong with the way you've worded your problem. Or your solution for that matter. It's just very tricky.
Log in to reply
@Michael Mendrin – Yes, I agree and think it's special to see the unique ratio for this kind of shape.
Suppose that F D = x , A F = x y , B E = b and C F = c for positive integers x , y , b , c . The first set of conditions tell us that b + c = 2 x y Then we know that D G = x ( y + 1 ) and C G = x y + c , so that x y and c are coprime and Pythagoras' Theorem applied to C F G tells us that y c = 2 x ( y + 1 ) Finally using similar triangles, we have 2 x ( y + 1 ) − A E b = x ( y + 2 ) c so that b ( y + 2 ) < 2 c ( y + 1 )
Since y and y + 1 are coprime, y must divide 2 x . Since x and c are coprime, c must divide 2 ( y + 1 ) . There are two cases to consider:
Thus the area A B C D is 2 1 × b × 2 x ( y + 1 ) − 2 1 × c × x ( y + 1 ) = 2 1 ( 2 b − c ) x ( y + 1 ) = 7 2