Evaluate This Limit
If x → 0 lim x sin x a e x − b cos x + c e − x = 2 ,
then find a + b + c .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
you're only allowed to use the L'Hopital's Rule when a lim is of the shape of 0/0 or inf/inf. I might be crazy but I don't see how you can use it here since this is of the form a-b+c/0. Maybe I'm just not seeing something here
Log in to reply
I see what you're saying. I guess I should have specified that we know the limit is of indeterminate form because the answer is a non-zero finite number, therefore L'Hopital's Rule can be used.
Log in to reply
The problem of using L"Hopital's rule here is that: lim g'(x) =0 where g(x)=xsinx and x -->0 and as i remember you can use this rule only when lim g'(x) is not 0. Correct me please if i'm wrong.
Log in to reply
@Liviu Tudor – But you could still have a situation in which lim f'(x)=0, which would generate another indeterminate form, setting up for a second use of L'Hopital's rule. In this second use, the denominator is now nonzero with direct substitution.
using series expansions,
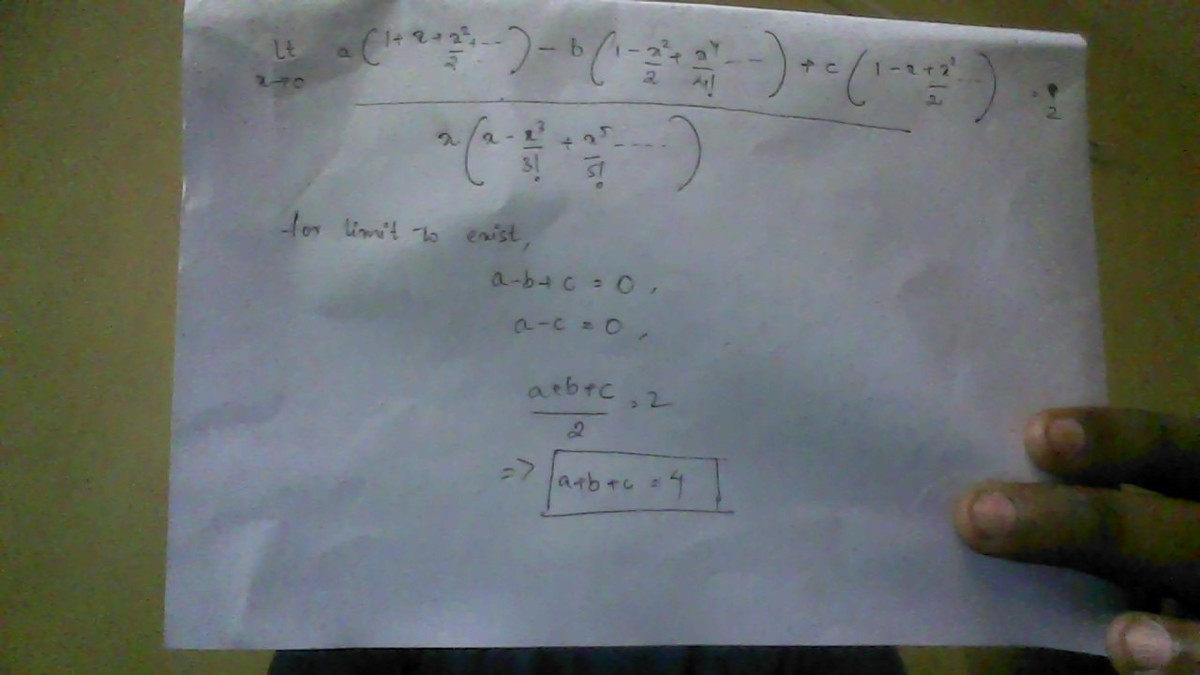
Use L'Hopital's Rule :
x → 0 lim x sin x a e x − b cos x + c e − x = x → 0 lim sin x + x cos x a e x + b sin x − c e − x = x → 0 lim 2 cos x − x sin x a e x + b cos x + c e − x = 2 a + b + c
2 a + b + c = 2 ∴ a + b + c = 4