Ex-Skews Me Sir
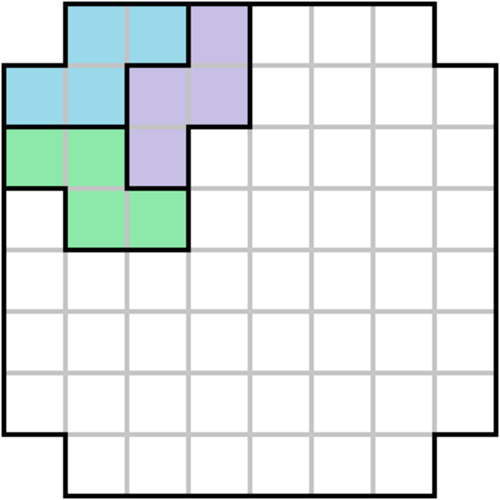
Is it possible to completely tile (without gaps or overlap) an 8 × 8 square with the 4 corners removed by different rotations and reflections of the skew tetromino ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Great solution! Are there any other colourings that work?
Log in to reply
I couldn't find any, but I also didn't think of your solution, so there's a good chance I missed another one, too.
By the way, I found a solution for the 6 x 6 square with the 4 corners removed, but I could not find a solution for the 10 x 10 square with the corners removed, and for the 10 x 10 neither mine nor your patterns prove it impossible. Do you have any insight on that?
Log in to reply
Not much. I'm pretty sure that either of our approaches work for a 4 n × 4 n square with the corners removed, because 1 6 n 2 − 4 is not a multiple of 8 (so in your colouring, the number of grey squares will be different to the number of white squares). But that doesn't work for 1 0 × 1 0 , or 6 × 6 for that matter. How did you solve 6 × 6 ?
Log in to reply
@Chris Lewis – I meant that the tiling is possible for the 6 x 6 square with the 4 corners removed:
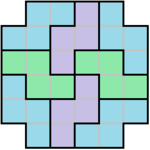
But I couldn't find a tiling for the 10 x 10 square with the 4 corners removed, and I couldn't find a way to prove it impossible, either.
Log in to reply
@David Vreken – Ha, I was just about to post the same tiling for 6x6 (I guess it's the only one)
Log in to reply
@Chris Lewis – Wow, the 10x10 is frustrating. Did you get anywhere with it? I wonder if there's an algorithmic approach that might help - mainly I'm thinking of whether it's possible to code tilings, but I suppose it may also be possible to look for colourings.
What's your hunch? Can a 10x10 be tiled?
Log in to reply
@Chris Lewis – I didn't get anywhere with it, but my hunch is that it cannot be tiled.
@David Vreken – Hello, I know that this is old but how are u making those diagrams? I am interested in trying the 10x10.
Log in to reply
@Razzi Masroor – I use MS Paint.
Log in to reply
@David Vreken – Another way is to use conditional formatting in Excel - if you draw a grid and apply a colour scale format to it then you just have to type in numbers to get different colours for the tiles.
That is a very clever coloring, nice! I couldn't come up with that... And that pun though! haha
Label the squares from
1
to
4
as follows:
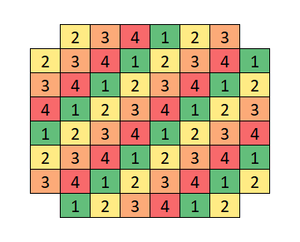
Any rotation of a "Z" skew tetromino (like the green or purple ones in the original diagram) always covers 1 , 2 , 3 , 4 in some order.
Any rotation of an "S" skew tetromino (like the blue one in the original diagram) always covers two pairs of numbers. Count each type of tile by the set of numbers it covers:
| Numbers covered | Count |
| 1 , 2 , 3 , 4 | A |
| 1 , 1 , 2 , 2 | B |
| 2 , 2 , 3 , 3 | C |
| 3 , 3 , 4 , 4 | D |
| 4 , 4 , 1 , 1 | E |
There are 1 5 ones and 1 6 twos in the grid. This means that A + 2 B + 2 E = 1 5 and A + 2 B + 2 C = 1 6
But the first of these implies A is odd, and the second that A is even; contradiction. So no such tiling is possible .
...I bet there's a better colouring to use, though.
Log in to reply
Nice solution! I'm not sure if I would call my solution better, but I did find a method that uses only two colors instead of four. I'll hold off on posting it, though, to see if you can find the same one I did. :-)
Log in to reply
You should probably just go ahead and post that one - I'm getting nowhere! I'd be interested to know if there's a good way to reverse engineer these colourings, though. For example, here, with two colours (say red and green, and say R cells are red), if x tiles cover no red cells and y cover one red cell, it doesn't work; the equations we get are something like x + y = 1 5 and y = R
which can't lead to a contradiction. But if x tiles cover no red cells and y cover two red cells, it's OK: x + y = 1 5 and 2 y = R so if R is odd, we win. Unfortunately I kept finding a mix of some tiles covering an odd number of red cells, which didn't work out.
Log in to reply
@Chris Lewis – Right, my pattern covers either 1 or 3 cells.
@Chris Lewis – Okay, I posted my solution.
Color the area as follows with 2 8 gray squares and 3 2 white squares:
Then there are two types of skew tetronimoes that can be placed on the board - one that covers 1 white square and 3 gray squares, and one that covers 3 white squares and 1 gray square:
Let x be the number of skew tetronimoes that cover 1 white square and 3 gray squares, and let y be the number of skew tetronimoes that cover 3 white squares and 1 gray square.
Since each skew tetronimo covers 4 squares, and since there are 8 ⋅ 8 − 4 = 6 0 squares, there are 4 6 0 = 1 5 total skew tetronimoes, so x + y = 1 5 .
Also, since 2 8 gray squares need to be covered, 3 x + y = 2 8 .
However, x + y = 1 5 and 3 x + y = 2 8 leads to ( x , y ) = ( 2 1 3 , 2 1 7 ) , a non-integer solution, which is not possible.
Therefore, the tiling is not possible .