Expansion problem!!
If the last term in the binomial expansion of ( 2 1 / 3 − 2 1 ) n is ( 3 3 5 1 ) lo g 3 8 , then what will the 5th term be?
The answer is 210.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Same and exactly the same method as I used. Cheers!
First, we simplify.
( 3 3 5 1 ) lo g 3 8 = 3 − 5 lo g 3 8 / 3 = 2 − 5 = ( 2 1 ) 1 0
This implies n = 1 0 . Now, by the binomial theorem, the 5th term will be
( 6 1 0 ) ( 2 1 / 3 ) 6 ( − 2 1 ) 1 0 − 6 = ( 6 1 0 ) = 2 1 0
Doesn't the question ask for the 5th term however? Also isn't the term you calculated above, the 6th term not the 7th term?
Log in to reply
It's the 7th term.
Because in the binomial theorem ( a + b ) n k = 0 ∑ n ( k n ) a k b n − k you are computing a total of 11 terms; since the convention is the expression above (even though you could switch the indices k and n − k if you wanted to) the 7th term is then at k = 6 .
The author probably made a typo, since the terms at k = 4 , 5 do not give an integral value (the input is integral). I've disputed the problem.
Edit: See Calvin's comment.
Log in to reply
Jake, you have your order of terms mixed up. The first term of ( a + b ) n is a n , which is not obtained by setting k = 0 in your expression.
Instead, it should be ( a + b ) n = ∑ k = 0 n ( k n ) a n − k b k .
This explains the discrepancy between your "7th term" and his "5th term".
Log in to reply
@Calvin Lin – Argh, yup. I've made the necessary change to the problem and my solution. Thanks.
I solve this using the binomial theorem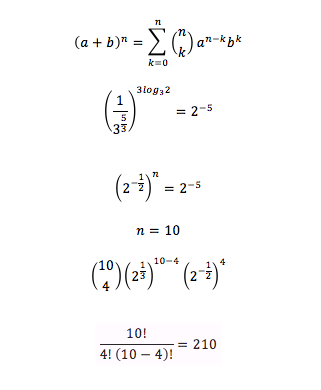 .
.