Expected Distance on a Circle

Calculus Level 5

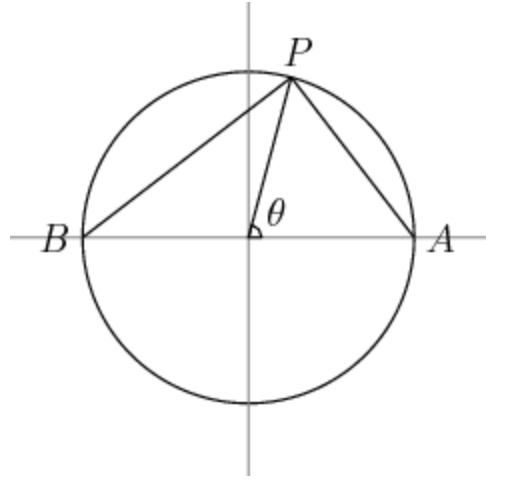
An angle θ \theta is chosen randomly in the interval [ 0 , 2 π ) [0,2\pi ) , and its corresponding point on the unit circle is plotted. Let this point be P P . Now let A = ( 1 , 0 ) A=(1,0) and B = ( − 1 , 0 ) B=(-1,0) .

Let the expected value of P A + P B − 2 PA+PB-2 be E E .

What is ⌊ 1000 E ⌋ \lfloor 1000E\rfloor ?


The answer is 546.

View wiki
Daniel Liu by Daniel Liu , 21, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Discussions for this problem are now closed

Jatin Yadav
May 4, 2014

The point can be taken as cos ⁡ θ , sin ⁡ θ \cos \theta, \sin \theta

PA + PB = ( 1 − cos ⁡ θ ) 2 + sin ⁡ 2 θ + ( 1 + cos ⁡ θ ) 2 + sin ⁡ 2 θ = 2 − 2 cos ⁡ θ + 2 + 2 cos ⁡ θ \sqrt{(1-\cos \theta)^2 + \sin^2 \theta} + \sqrt{(1+\cos \theta)^2 + \sin^2 \theta} = \sqrt{2 - 2\cos \theta } + \sqrt{2 + 2 \cos \theta}

= 2 ( ∣ sin ⁡ θ 2 ∣ + ∣ cos ⁡ θ 2 ∣ ) 2(|\sin \frac{\theta}{2}|+|\cos \frac{\theta}{2}|)

The probability that the point is chosen between θ \theta , and θ + d θ \theta + d \theta is d θ 2 π \dfrac{d \theta}{2 \pi}

Hence, expected value of P A + P B − 2 PA+PB-2 is ∫ 0 2 π 2 ( ∣ sin ⁡ θ 2 ∣ + ∣ cos ⁡ θ 2 ∣ − 1 ) d θ 2 π = 8 π − 2 \dfrac{\int_{0}^{2\pi} 2(|\sin \frac{\theta}{2}|+|\cos \frac{\theta}{2}|-1) d \theta}{2 \pi} = \dfrac{8}{\pi} - 2

Hence, our answer is ⌊ 1000 ( 8 π − 2 ) ⌋ = 546 \bigg \lfloor 1000(\frac{8}{\pi} - 2) \bigg \rfloor = 546

24 Helpful 0 Interesting 0 Brilliant 0 Confused

How many points are there between x and x+dx?(here theta)

A Former Brilliant Member - 7 years, 1 month ago

@Anup Navin

The notation d x dx means taking the limit as d x dx approaches 0. So as d x dx approaches 0, x + d x x + dx approaches x x and so, taking the limit, we find something very interesting.

Even as d x dx becomes smaller and smaller, there are still an infinite number of points between x x and x + d x x + dx . However, when d x = 0 dx = 0 , we find no points between x x and x + d x x + dx . So what is the number of points between x x and x + d x x + dx ? Is this question very well-defined?

Colin Tang - 7 years, 1 month ago

so, assuming that the probability that the point is chosen between x and x+dx is still an approximation?

A Former Brilliant Member - 7 years, 1 month ago
Trevor B.
May 4, 2014

The point P P is going to be located at ( cos ⁡ θ , sin ⁡ θ ) . (\cos\theta,\sin\theta). By appling the distance formula to both points, we find this. P A + P B = ( 1 − cos ⁡ θ ) 2 + sin ⁡ 2 θ + ( − 1 − cos ⁡ θ ) 2 + sin ⁡ 2 θ = 1 − 2 cos ⁡ θ + cos ⁡ 2 θ + sin ⁡ 2 θ + 1 + 2 cos ⁡ θ + cos ⁡ 2 θ + sin ⁡ 2 θ = 2 − 2 cos ⁡ θ + 2 + 2 cos ⁡ θ \begin{aligned} PA+PB&=\sqrt{(1-\cos\theta)^2+\sin^2\theta}+\sqrt{(-1-\cos\theta)^2+\sin^2\theta}\\ &=\sqrt{1-2\cos\theta+\cos^2\theta+\sin^2\theta}+\sqrt{1+2\cos\theta+\cos^2\theta+\sin^2\theta}\\ &=\sqrt{2-2\cos\theta}+\sqrt{2+2\cos\theta} \end{aligned} Now we have to find the average value of this as theta ranges from 0 0 to 2 π . 2\pi. Start by simplifying the integral a little bit. 1 2 π ∫ 0 2 π 2 − 2 cos ⁡ θ + 2 + 2 cos ⁡ θ d θ = 2 2 π ∫ 0 2 π 1 − cos ⁡ θ + 1 + cos ⁡ θ d θ = 2 2 π ( ∫ 0 2 π 1 − cos ⁡ θ d θ + ∫ 0 2 π 1 + cos ⁡ θ d θ ) \begin{aligned} \dfrac{1}{2\pi}\int_0^{2\pi}\sqrt{2-2\cos\theta}+\sqrt{2+2\cos\theta}\text{ }d\theta&=\dfrac{\sqrt{2}}{2\pi}\int_0^{2\pi}\sqrt{1-\cos\theta}+\sqrt{1+\cos\theta}\text{ }d\theta\\ &=\dfrac{\sqrt{2}}{2\pi}\left(\int_0^{2\pi}\sqrt{1-\cos\theta}\text{ }d\theta+\int_0^{2\pi}\sqrt{1+\cos\theta}\text{ }d\theta\right) \end{aligned} Those integrals aren't going to be easy to solve directly, so simplify the radicals to something we can make a u -substitution u\text{-substitution} out of.

1 − cos ⁡ θ = 1 − cos ⁡ 2 θ 1 + cos ⁡ θ = ∣ sin ⁡ θ ∣ 1 + cos ⁡ θ \sqrt{1-\cos\theta}=\dfrac{\sqrt{1-\cos^2\theta}}{\sqrt{1+\cos\theta}}=\dfrac{|\sin\theta|}{\sqrt{1+\cos\theta}}

1 + cos ⁡ θ = 1 − cos ⁡ 2 θ 1 − cos ⁡ θ = ∣ sin ⁡ θ ∣ 1 − cos ⁡ θ \sqrt{1+\cos\theta}=\dfrac{\sqrt{1-\cos^2\theta}}{\sqrt{1-\cos\theta}}=\dfrac{|\sin\theta|}{\sqrt{1-\cos\theta}}

To avoid dealing with improper integrals, you can say that ∫ 0 2 π ∣ sin ⁡ θ ∣ 1 ± cos ⁡ θ d θ = ∫ 0 π 2 4 sin ⁡ θ 1 ± cos ⁡ θ d θ \displaystyle\int_0^{2\pi}\dfrac{|\sin\theta|}{\sqrt{1\pm\cos\theta}}\text{ }d\theta=\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{4\sin\theta}{\sqrt{1\pm\cos\theta}}\text{ }d\theta

2 2 π ( ∫ 0 2 π 1 − cos ⁡ θ d θ + ∫ 0 2 π 1 + cos ⁡ θ d θ ) = 2 2 π ( ∫ 0 π 2 sin ⁡ θ 1 + cos ⁡ θ d θ + ∫ 0 π 2 sin ⁡ θ 1 − cos ⁡ θ d θ ) \dfrac{\sqrt{2}}{2\pi}\left(\int_0^{2\pi}\sqrt{1-\cos\theta}\text{ }d\theta+\int_0^{2\pi}\sqrt{1+\cos\theta}\text{ }d\theta\right) =\dfrac{2\sqrt{2}}{\pi}\left(\int_0^\frac{\pi}{2}\dfrac{\sin\theta}{\sqrt{1+\cos\theta}}\text{ }d\theta+\int_0^\frac{\pi}{2}\dfrac{\sin\theta}{\sqrt{1-\cos\theta}}\text{ }d\theta\right)

Let's solve these integrals one at a time.

∫ 0 π 2 sin ⁡ θ 1 + cos ⁡ θ d θ = ∫ 2 1 − d u u = ∫ 1 2 d u u = 2 u ∣ 1 2 = 2 2 − 2 \begin{aligned} \int_0^\frac{\pi}{2}\dfrac{\sin\theta}{\sqrt{1+\cos\theta}}\text{ }d\theta&=\int_2^1\dfrac{-du}{\sqrt{u}}\\ &=\int_1^2\dfrac{du}{\sqrt{u}}\\ &=\left.2\sqrt{u}\right|^2_1\\ &=2\sqrt{2}-2 \end{aligned} ∫ 0 π 2 sin ⁡ θ 1 − cos ⁡ θ d θ = ∫ 0 1 d u u = 2 u ∣ 0 1 = 2 \begin{aligned} \int_0^\frac{\pi}{2}\dfrac{\sin\theta}{\sqrt{1-\cos\theta}}\text{ }d\theta&=\int_0^1\dfrac{du}{\sqrt{u}}\\ &=\left.2\sqrt{u}\right|^1_0\\ &=2 \end{aligned} Summing these together, we see this. ∫ 0 π 2 sin ⁡ θ 1 + cos ⁡ θ d θ + ∫ 0 π 2 sin ⁡ θ 1 − cos ⁡ θ d θ = 2 2 − 2 + 2 = 2 2 \int_0^\frac{\pi}{2}\dfrac{\sin\theta}{\sqrt{1+\cos\theta}}\text{ }d\theta+\int_0^\frac{\pi}{2}\dfrac{\sin\theta}{\sqrt{1-\cos\theta}}\text{ }d\theta=2\sqrt{2}-2+2=2\sqrt{2}

Remembering the scalar from earlier, we find this. 2 2 π ( ∫ 0 π 2 sin ⁡ θ 1 + cos ⁡ θ d θ + ∫ 0 π 2 sin ⁡ θ 1 − cos ⁡ θ d θ ) = 2 2 π × 2 2 = 8 π \dfrac{2\sqrt{2}}{\pi}\left(\int_0^\frac{\pi}{2}\dfrac{\sin\theta}{\sqrt{1+\cos\theta}}\text{ }d\theta+\int_0^\frac{\pi}{2}\dfrac{\sin\theta}{\sqrt{1-\cos\theta}}\text{ }d\theta\right)=\dfrac{2\sqrt{2}}{\pi}\times2\sqrt{2}=\boxed{\dfrac{8}{\pi}}

The expected value for P A + P B PA+PB is 8 π ≈ 2.54647 … , \frac{8}{\pi}\approx2.54647\ldots, so E ≈ 0.54647 … E\approx0.54647\ldots and ⌊ 1000 E ⌋ = 546 \lfloor1000E\rfloor=\boxed{546}

8 Helpful 0 Interesting 0 Brilliant 0 Confused

There isn't a need to use the distance formula. The lengths are obvious from the sketch. It can be seen that ∠ P A B = π / 2 − θ / 2 \angle PAB=\pi/2-\theta/2 . Since Δ P A B \Delta PAB is a right angled triangle, P A = 2 ∣ sin ⁡ ( θ / 2 ) ∣ PA=2|\sin(\theta/2)| . Similarly, P B = 2 ∣ cos ⁡ ( θ / 2 ) ∣ PB=2|\cos(\theta/2)| .

Pranav Arora - 7 years, 1 month ago

Excellent.

Finn Hulse - 7 years, 1 month ago

Another path you can take after arriving at 1 + cos ⁡ θ \sqrt{1+\cos\theta} and 1 − cos ⁡ θ \sqrt{1-\cos\theta} is using the reverse half-angle identity to get 1 + cos ⁡ θ = 2 ∣ cos ⁡ ( θ 2 ) ∣ \sqrt{1+\cos\theta}=2\left|\cos \left(\dfrac{\theta}{2}\right)\right| and 1 − cos ⁡ θ = 2 ∣ sin ⁡ ( θ 2 ) ∣ \sqrt{1-\cos\theta}=2\left|\sin \left(\dfrac{\theta}{2}\right)\right| .

We can also get rid of the absolute value signs by noting that we just need to take the integral from 0 0 to π \pi because of symmetry, which forces cos ⁡ ( θ 2 ) \cos \left(\dfrac{\theta}{2}\right) and sin ⁡ ( θ 2 ) \sin \left(\dfrac{\theta}{2}\right) to both be positive.

You also typoed in your 4th to last equation: it should be 2 2 − 2 2\sqrt{2}-2 , not 2 2 − 1 2\sqrt{2}-1 .

Daniel Liu - 7 years, 1 month ago

You can restrict the integration still further because there is symmetry between placing the point P in the first or second quadrant; so you can just integrate from 0 to π 2 \frac{\pi}{2} and skip the absolute value brackets entirely. Also, as long as you're going to use the half-angle trigonometric terms, you can write their sum as 2 sin ⁡ θ 2 + 2 cos ⁡ θ 2 = 2 2 ( 2 2 sin ⁡ θ 2 + 2 2 cos ⁡ θ 2 ) 2 \sin \frac{\theta}{2} + 2 \cos \frac{\theta}{2} = 2\sqrt{2} \ ( \frac{\sqrt{2}}{2} \sin \frac{\theta}{2} + \frac{\sqrt{2}}{2} \cos \frac{\theta}{2} ) = 2 2 [ sin ⁡ θ 2 cos ⁡ ( π 4 ) + cos ⁡ θ 2 sin ⁡ ( π 4 ) ] = 2\sqrt{2} \ [ \ \sin \frac{\theta}{2} \cos ( \frac{\pi}{4} ) + \cos \frac{\theta}{2} \sin ( \frac{\pi}{4} ) \ ] = 2 2 sin ⁡ ( θ 2 + π 4 ) = 2\sqrt{2} \ \sin (\frac{\theta}{2} + \frac{\pi}{4} ) [which uses the "angle-addition" formulas]. This simplifies the integrand considerably.

Gregory Ruffa - 7 years, 1 month ago

Well, that certainly would have saved a bit of work! \text{ } ;)

Fixed!

Trevor B. - 7 years, 1 month ago

are you sure it REQUIRES calculus?

Nathan Ramesh - 7 years, 1 month ago

Seeing it requires you to find the average value of a continuous curve, I'd say yes. @Trevor B. knows more about this than me, I'm still a noob. What do you say?

Daniel Liu - 7 years, 1 month ago

I believe it does, but do you have a non-calculus solution?

Trevor B. - 7 years, 1 month ago

@Trevor B. – no i suck at math idk any calculus so i was just wondering

Nathan Ramesh - 7 years, 1 month ago

I must say that taking the modulus value is absolute necessary. First time I solved it, I did not take modulus and got the expected value as zero!

Avineil Jain - 7 years, 1 month ago

For any conic including circle PA+PB is always constant ...... Then what is the need of using integration ?

Kanthi Deep - 7 years, 1 month ago

No, that would be true if A A and B B were the foci. Wht you are thinking of are the foci of an ellipse. Additionally, in a circle, the only thing constant is A P 2 + B P 2 AP^2+BP^2 .

Trevor B. - 7 years, 1 month ago

Thanks I forgot it

Kanthi Deep - 7 years, 1 month ago

Search wolframalpha for the following query have the answer presented to you-- floor(1000*(integrate 2abs(sin(x/2))+2abs(cos(x/2))-2 from 0 to 2pi)/(2pi))

Connor Kenway - 7 years, 1 month ago

actually wat is integration

Suvir M - 7 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...