Exploring electromagnetism 1!
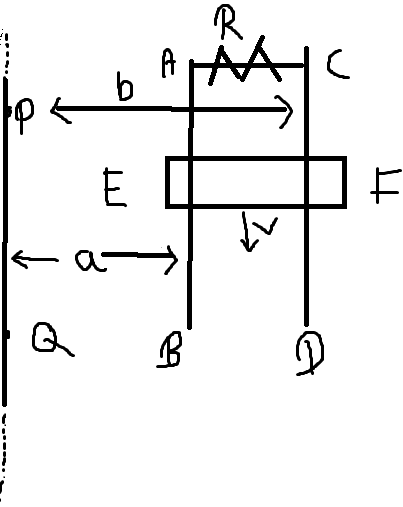 is an infinite conductor carrying a current
.
and
are smooth conducting rods on which a conductor
moves with constant velocity
as shown. The resistance of the resistor is
.
is an infinite conductor carrying a current
.
and
are smooth conducting rods on which a conductor
moves with constant velocity
as shown. The resistance of the resistor is
.
Find the magnitude of force in Newton needed to maintain constant speed of .
Details and assumptions:
- Take the volumetric susceptibility of the medium surrounding the system to be 0.
- Multiply the magnitude of force by and then report the answer.
- Give answer to 3 decimal places.
The answer is 21.2075.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First we calculate the magnetic field due to the infinite conductor in a perpendicular distance l from it: B = − 2 π l μ I k ^
Then we calculate the emf in the conductor E F : ϵ = ∫ a b ( v × B ) ⋅ d l = 2 π v μ I ∫ a b l d l = 2 π v μ I ln ( a b )
Next, we calculate the induced current: I ′ = R ϵ = 2 π R v μ I ln ( a b )
Then we calculate the magnetic force: F M = I ′ ∫ a b d l × B = 2 π I ′ μ I ∫ a b l d l j ^ = 2 π I ′ μ I ln ( a b ) j ^ = R v ( 2 π μ I ln ( a b ) ) 2 j ^
Finally, we muts apply another force F with the same magnitude tham F M but in the opposite direction ( − j ^ ) to keep moving the conductor with the constant velocity. Substituting values we get: F = 1 0 Ω 1 0 m/s ( 2 π 4 π × 1 0 − 7 A 2 N × 1 0 A ln ( 2 m 2 0 m ) ) 2 F ≈ 2 . 1 2 0 7 5 × 1 0 − 1 1 N
So, our answer is 2 1 . 2 0 7 5 .