Expodical: Repost

Algebra Level pending

$\sqrt{x^{x^{x...}}\sqrt{x^{x^{x...}}\sqrt{x^{x^{x...}}...}}}^{\sqrt{x^{x^{x...}}\sqrt{x^{x^{x...}}\sqrt{x^{x^{x...}}...}}}^{\sqrt{x^{x^{x...}}\sqrt{x^{x^{x...}}\sqrt{x^{x^{x...}}...}}}^{.^{.^{.}}}}}=16$

$x^{16 {\sqrt[16]{16}}} =?$

DETAILS AND ASSUMPTIONS:

x is a positive real number.
Look only for positive, real solutions.

Acknowledgement:

The original problem was incorrectly interpreted by the solvers; the expression is exponentiated into itself infinitely many times, not just three (note the dot-dot-dot on top). Wrong answers were entered, but were accepted by the system as correct (because I originally solved my own problem incorrectly).

I apologize for the mishap.

(the exponent reads "16 times the 16th root of 16")

The answer is 16.

1 solution

John M.
Oct 11, 2014

Let $\sqrt{x^{x^{x...}}\sqrt{x^{x^{x...}}\sqrt{x^{x^{x...}}...}}}=X$ . Then,

$X^{X^{X^{.^{.^{.}}}}}=16$

$X^{(X^{X^{.^{.^{.}}}})}=16$

$X^{16}=16$

$X=\sqrt[16]{16}$

And so,

$\sqrt{x^{x^{x...}}\sqrt{x^{x^{x...}}\sqrt{x^{x^{x...}}...}}}=\sqrt[16]{16}$

Let $x^{x^{x...}}=@$ . Then,

$\sqrt{@\sqrt{@\sqrt{@...}}}=\sqrt[16]{16}$

$@\sqrt{@\sqrt{@\sqrt{@...}}}=\sqrt[8]{16}$

$@\cdot \sqrt[16]{16} = \sqrt[8]{16}$

$@=\sqrt[16]{16}$

And so,

$x^{x^{x...}}=\sqrt[16]{16}$

$x=\sqrt[16]{16}^{\frac{1}{\sqrt[16]{16}}}$

Some power clashing reveals

$x^{16\sqrt[16]{16}} =\boxed{16}$

GENERAL CASES:

$\boxed{\sqrt{N\sqrt{N\sqrt{N\sqrt{N...}}}}=N}$

Proof:

$\sqrt{N\sqrt{N\sqrt{N\sqrt{N...}}}}=N$

$\Rightarrow N\sqrt{N\sqrt{N\sqrt{N...}}}=N^2$

$\Rightarrow N\cdot N=N^2$

$\Rightarrow \boxed{N^2=N^2}$

$\forall N$

$N^{N^{N^{.^{.^{.}}}}}=M$

$\Rightarrow \boxed{N=M^{\frac{1}{M}}}$

PROOF:

$N^{N^{N^{.^{.^{.}}}}}=M$

$N^M=M$

$N=M^{\frac{1}{M}}$

$\forall N, M$

$\sqrt{N^{N^{N...}}\sqrt{N^{N^{N...}}\sqrt{N^{N^{N...}}...}}}^{\sqrt{N^{N^{N...}}\sqrt{N^{N^{N...}}\sqrt{N^{N^{N...}}...}}}^{\sqrt{N^{N^{N...}}\sqrt{N^{N^{N...}}\sqrt{N^{N^{N...}}...}}}^{.^{.^{.}}}}}=M$

PROOF:

$\sqrt{N^{N^{N...}}\sqrt{N^{N^{N...}}\sqrt{N^{N^{N...}}...}}}=M^{\frac{1}{M}}$

$N^{N^{N^{...}}}=M^{\frac{1}{M}}$

$N=M^{ { \frac { 1 }{ M } }^{ \frac { 1 }{ M^{ \frac { 1 }{ M } } } } }$

$N=M^{ { \frac { 1 }{ M\cdot M^{\frac{1}{M}}}}}$

$\forall N, M$

I should bring to your attention that this infinite tower function is a particularly tricky function, and in fact, it can't ever have a finite value greater than e = 2.718.... If you plug in 16^(1/16) into this infinite tower function, you won't get 16, but more like 1.23961.... This is one bad-ass function to mess around with.

Michael Mendrin - 6 years, 8 months ago

You sure? My steps do look convincing enough, though. If you look at my general cases - even more. If we go backwards (raise x into itself infinitely many times, then plug the result for all x towers, and compute the infinite radical, and then the infinite radical tower), I think we'll get $16$ .

(sorry for my lack of replies. I took the SAT yesterday, which I was preparing for the whole week. This week I'll be making up all the work I'm behind on in my AP Stats and AP Physics C - I got like 20% in those classes. And my 5 other AP (one isn't really AP, but it sure is in my eyes (Multivariable Calc)).

I'll check later. If someone else could do that for me that'd be great.

Cheers,

John M. - 6 years, 8 months ago

John, I've seen a lot of "fallacious proofs" posted in Brilliant as a fun exercise. But I think this one takes the cake, in that it's very difficult to show why it fails. It's a real head-scratcher. But do try to compute ${ \sqrt [ 16 ]{ 16 } }^{ { \sqrt [ 15 ]{ 16 } }^{ { \sqrt [ 16 ]{ 16 } }^{ ... } } }$ and see what you actually get.

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin Sir, please tell more about this function. What is the value of the infinite tower at $x=\sqrt{2}$ ? Thanks.

Satvik Golechha - 6 years, 8 months ago

It's $2$ , as expected. Like I said, it's a very tricky function! To get a start on understanding why it's so tricky, let's have a look at the function $f(x)=x^{ \dfrac { 1 }{ x } }$

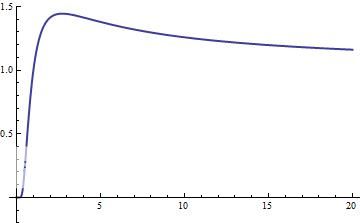Root Function

Notice that it peaks at $x=e^{ \dfrac { 1 }{ e } }$ ? And that any greater $x$ results in a value that can be found for a $x$ less than this?

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin – @John Muradeli The issue is that you are assuming that there is a real value of $X$ which satisfies the equation. As Michael pointed out, such an assumption is not necessarily true.

Your proofs are not actually valid yet. They represent a simplistic "algebraic substitution", which assumes that the answer exists (and is real). This allows us to calculate a real value answer, but you still have to substitute it back and explain why it is true.

For example, when you manipulated the equations, you squared terms (and rooted terms) which could introduce extraneous solutions. Using the same appraoch as you did, I could show that $\sqrt{N\sqrt{N\sqrt{N\sqrt{\ldots} }}} = - N$ , since the first step is squaring which gets rid of the negative sign.

With infinite exponentiation, these are actually calculated as limits, instead of "pure algebraic manipulations". Your approach is akin to using induction, but induction does not allow us to reach infinity.

Calvin Lin Staff - 6 years, 8 months ago

@Calvin Lin – A-ah. My fears confirmed.

Now, I don't know what the reality of it is, but, if I add (Assume positive real solutions only), will it solve the problem?

John M. - 6 years, 8 months ago

@John M. – John, simply put, the infinite tower can never have a value like 16. It doesn't matter what you have in the infinite tower, you just can't get up there. Just like in relativistic physics, there's a speed limit of c, infinite towers have a limit of e. OR it is immediately infinite right after x=e^(1/e)

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin – Err I don't get it. What if $x=2$ ? Then where's your $e$ ?

Or are you saying that the tower's finite limit is $e$ ? In this case, my pet Wolf revea- ... wait... WHAT? Umm.... O_O

Ok so... As I plug in more and more, it rises, but then actually slowly descends (kinda like your graph over there). What the heck?? Wow this is amazing! So does this mean the Infinite Power! problem is wrong? Or does it mean that if the right side were 3 then it would've been? But this is like... so contrary to my proofs!

That's why you don't mess with teh freakin infinity...

EDIT:

But this isn't x^x^x... this is more complicated than that. This is infinite radicals that contain x^x^x ... this doesn't mean that those radicals also have to obey this e rule.

... or do they?

John M. - 6 years, 8 months ago

@Michael Mendrin – Question:

Is $^{-4}x$ the multiplicative identity of $^{4}x$ ?

( $^{-4}x \cdot x^{x^{x^{x}}}=1$ )

Question 2:

$^{-\infty}x \cdot ^{\infty} x = 1$ ?

Reasoning:

$^{\infty}x=x^{x^{x^{x...}}}=CanBeConstant$ , so, if the negative counterpart is simply its denominator, cancel.

John M. - 6 years, 8 months ago

@John M. – I have to think about what negative tetration even means. I do have work to do today, so I'll have to get back to this later, and have a look at your proposed [pretty wild] problem. I don't think we can generalize the idea of positive tetration to include negative, fractional, irrational, or complex tetration, at least not without a LOT of additional conditions or definitions.

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin – Take your time. But DONT FORGET! Last time you forgot on the Yin-Yang problem.

John M. - 6 years, 8 months ago

@John M. – There was a Yin-Yang problem?

Edit: Oh, I see that now, yeah, I forgot about it. But first, let me pull together the solution to my Mighty Mosquito problem, it's going to be a little difficult to explain it concisely enough.

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin – Take as long as you want (just... you know... before I rule the world. Then I'll be busy.). And the mosquito problem - you better have some explanations on how the answer is independent of the distance between the black hole and the train and the train's initial speed! Really wanna see the solution.

Rock on, Mathopedia!

John M. - 6 years, 8 months ago

@John M. – The fact that it's independent of things like velocity, distances, etc. is probably the least surprising thing about the answer. I've waited a real long time to pose this specific problem.

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin – Now might be a good time :D

@Michael Mendrin

John M. - 6 years ago

@Michael Mendrin – Final question:

Would I get bombed if I posted THIS ?

(ahead note: Ignore "3 solutions" - I forgot the infinite radicals cancel with x when I made the image. )

Solution:

Denominator x's cancel by assumption 2.
...x & x... cancel with x^(-infinity) by assumption 2.
^-infty x and x^x^x... cancel (or not, depending on your response to my other questions)
infinite x radicals and x's cancel.
...^x^x^x x cancels with ...^x^x^x x x^x^x^x....

And we're left with just the thing in the middle. This is just x^x^x^... but with (1/x). So set that equal to e^(1/e), and invert to get x.

So, will those cancelations be legal, or should I simplify the problem and trim the fat? And if so, tell me all the fat I HAVE TO trim. And preferribly if I got get rid of assumption 2.

Cheers!

John M. - 6 years, 8 months ago

@Michael Mendrin – Thanks sir, but I'm still confused as to why we can get two values. What shall I answer when my friend asks what $\sqrt{2}^{\sqrt{2}^{\sqrt{2}...}}$ is? I get both 2 and 4. Sorry if I made a blunder somewhere... I'm new to this. Thanks.

Satvik Golechha - 6 years, 8 months ago

@Satvik Golechha – If you look at my post, the issue with relying on just algebraic manipulations, is that it merely gives you a possible answer.

As you mentioned, since $\sqrt{2} ^ 4 = 4$ and $\sqrt{2} ^2 = 2$ , solving for $\sqrt{2} ^ x = x$ would give multiple solutions. However, there is clearly at most 1 answer that it could be (and that's even assuming that there is an answer).

The correct approach, is to understand this as a limit. If we calculate: $\sqrt{2} \approx 1.414$ ,
$\sqrt{2} ^ \sqrt{2} \approx 1.632$ ,
$\sqrt{2} ^ { \sqrt{2} ^ \sqrt{2} } \approx 1.7608$ , ....

The "graphical" approach, is to look at the convergence of the iterated function $y = \sqrt{2} ^ x$ , starting with the initial value of $x_0 = \sqrt{2}$ , and you see that it will converge to $2$ .

It is possible to rigourise this using calculus, where the ideas involve formalizing the graphical approach.

Calvin Lin Staff - 6 years, 8 months ago

@Calvin Lin – In other words, this problem is invalid (and hence the rating nerf).

So is there no solution to this? Should I take it down?

Does this also invalidate the "Infinite Power!" problem? Or it's just my problem that's too big to be solved? And why $\sqrt{2}^x=x$ can't have more than 1 solutions?

~J@M

John M. - 6 years, 8 months ago

Sorry for the excess repost spam, everyone. Had to make the answer as simple as possible.

John M. - 6 years, 8 months ago

Expodical: Repost

The answer is 16.

1 solution

0 pending reports